{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении
системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$
Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$
Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$
Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
сопротивления через силу тока и напряжение
Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Многообразие устройств электротехники
Электрический ток
Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.
Электрическое напряжение
Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.
Сопротивление
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Мощность
Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Закон Ома и его основатель
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Единицы измерения в формуле
Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:
Общепринятые обозначения, согласно международной системе измерения СИ:
- Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
- Сила тока – Ампер. Обозначается символом А;
- Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
- Электрическая мощность – Ватт. Обозначается как Вт или W.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Лампа накаливания
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Правило для запоминания расчетов
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Зависимость сопротивления воды от содержания солей
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
По какой формуле определяется напряжение
Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:
- Ток и сопротивление – U=I∙R;
- Ток и мощность – U=P/I;
- Мощность и сопротивление – U=√P∙R
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.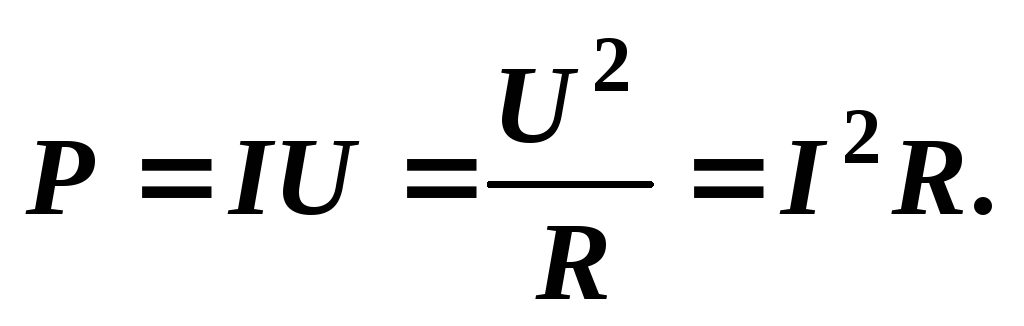
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Гидравлическая аналогия
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Один из самых распространенных авометров
Типичные напряжения
Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:
- Бытовая сеть –220В;
- Бортовая сеть автомобиля – 12 или 24В;
- Батареи и аккумуляторы – 1.5, 3 или 9В.
Потенциал Гальвани
В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.
Видео
Глава 21.
 Электрический ток. Законы Ома и Джоуля-Ленца
Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21. 2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21.3) |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21.4) |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21.6) |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21. 1.2)
1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21. 7). Имеем
7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
Цепь переменного синусоидального тока c частотой ω.
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.
Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети
Закон Ома для цепей переменного тока:
|
Закон Ома | Физика
В предыдущих параграфах были рассмотрены три величины, характеризующие протекание электрического тока в цепи,— сила тока I, напряжение U и сопротивление R. Между этими величинами существует определенная связь. Закон, выражающий эту связь, был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя.
Выделим в произвольной электрической цепи участок, обладающий сопротивлением R и находящийся под напряжением U (рис. 37). Согласно закону Ома:
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Математически закон Ома записывается в виде следующей формулы:
I = U/R (14.1)
Закон Ома позволяет установить, что будет происходить с силой тока на участке цепи при изменении его сопротивления или напряжения.
1. При неизменном сопротивлении сила тока прямо пропорциональна напряжению: чем больше напряжение U на концах участка цепи, тем больше сила тока I на этом участке. Увеличив (или уменьшив) напряжение в несколько раз, мы во столько же раз увеличим (или уменьшим) силу тока.
Увеличив (или уменьшив) напряжение в несколько раз, мы во столько же раз увеличим (или уменьшим) силу тока.
Проиллюстрируем эту закономерность на опыте. Соберем электрическую цепь из источника тока, лампы, амперметра и ключа (рис. 38, а). В качестве источника тока будем использовать устройство, позволяющее регулировать выходное напряжение от 4 до 12 В. Измеряя силу тока в цепи при разных напряжениях, можно убедиться в том, что она действительно пропорциональна напряжению.
2. При неизменном напряжении сила тока обратно пропорциональна сопротивлению: чем больше сопротивление R участка цепи, тем меньше сила тока I в нем.
Для проверки этой закономерности заменим в используемой цепи лампу на магазин сопротивлений (рис. 38, б). Измеряя силу тока при разных сопротивлениях, мы увидим, что сила тока I и сопротивление R действительно находятся в обратно пропорциональной зависимости.
При уменьшении сопротивления сила тока возрастает. Если сила тока превысит допустимое для данной цепи значение, включенные в нее приборы могут выйти из строя; провода при этом могут раскалиться и стать причиной пожара. Именно такая ситуация возникает при коротком замыкании. Так называют соединение двух точек электрической цепи, находящихся под некоторым напряжением, коротким проводником, обладающим очень малым сопротивлением.
Короткое замыкание может возникнуть при соприкосновении оголенных проводов, при небрежном ремонте проводки под током, при большом скоплении пыли на монтажных платах и даже при случайном попадании какого-нибудь насекомого внутрь прибора.
На законе Ома основан экспериментальный способ определения сопротивления. Из формулы (14.1) следует, что
R = U/I (14.2)
Поэтому для нахождения сопротивления R участка цепи надо измерить на нем напряжение U, затем силу тока I, после чего разделить первую из этих величин на вторую. Соответствующая этому схема цепи изображена на рисунке 39.
Если, наоборот, известны сопротивление R и сила тока I на участке цепи, то закон Ома позволяет рассчитать напряжение U на его концах. Из формулы (14.1) получаем
U = IR (14.3)
Чтобы найти напряжение U на концах участка цепи, надо силу тока I на этом участке умножить на его сопротивление R.
Опубликовав книгу, в которой излагался открытый им закон «Теоретические исследования электрических цепей», Георг Ом написал, что «рекомендует ее добрым людям с теплым чувством отца, не ослепленного обезьяньей любовью к детям, но довольствующегося указанием на открытый взгляд, с которым его дитя смотрит на злой мир». Мир действительно оказался для него злым, и уже через год после выхода его книги в одном из журналов появилась статья, в которой работы Ома были подвергнуты уничтожающей критике. «Тот, кто благоговейными глазами взирает на вселенную,— говорилось в статье,— должен отвернуться от этой книги, являющейся плодом неисправимых заблуждений, преследующих единственную цель — умалить величие природы».
Злобные и безосновательные нападки на Ома не прошли бесследно. Теорию Ома не приняли. И вместо продолжения научных исследований он должен был тратить время и энергию на полемику со своими оппонентами. В одном из своих писем Ом написал: «Рождение «Электрических цепей» принесло мне невыразимые страдания, и я готов проклясть час их зарождения».
Но это были временные трудности. Постепенно, сначала в России, а затем и в других странах, теория Ома получила полное признание. Закон Ома внес такую ясность в правила расчета токов и напряжений в электрических цепях, что американский ученый Дж. Генри, узнав об открытиях Ома, не удержался от восклицания: «Когда я первый раз прочел теорию Ома, то она мне показалась молнией, вдруг осветившей комнату, погруженную во мрак».
??? 1. Сформулируйте закон Ома. 2. Как изменится сила тока на участке цепи, если при неизменном сопротивлении увеличить напряжение на его концах? 3. Как изменится сила тока, если при неизменном напряжении увеличить сопротивление участка цепи? 4. Как с помощью вольтметра и амперметра можно измерить сопротивление проводника? 5. По какой формуле находится напряжение, если известны сила тока и сопротивление данного участка? 6. Что называют коротким замыканием? Почему при этом увеличивается сила тока? 7. Объясните причину короткого замыкания в ситуациях, изображенных на рисунке 40.
Как с помощью вольтметра и амперметра можно измерить сопротивление проводника? 5. По какой формуле находится напряжение, если известны сила тока и сопротивление данного участка? 6. Что называют коротким замыканием? Почему при этом увеличивается сила тока? 7. Объясните причину короткого замыкания в ситуациях, изображенных на рисунке 40.
Сила тока | Самое простое объяснение, формула, единица измерения
Сила тока с точки зрения гидравлики
Думаю, вы не раз слышали такое словосочетание, как “сила тока“. А для чего нужна сила? Ну как для чего? Чтобы совершать полезную или бесполезную работу. Главное, чтобы что-то делать. Каждый из нас обладает какой-либо силой. У кого-то сила такая, что он может одним ударом разбить кирпич в пух и в прах, а другой не сможет поднять даже соломинку. Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Представьте себе шланг, с помощью которого вы поливаете свой огород
Давайте теперь проведем аналогию. Пусть шланг – это провод, а вода в нем – электрический ток. Мы чуть-чуть приоткрыли краник и вода сразу же побежала по шлангу. Медленно, но все-таки побежала. Сила струи очень слабая.
А давайте теперь откроем краник на полную катушку. В результате струя хлынет с такой силой, что можно даже полить соседский огород.
В обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете ведро. Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Разберем еще один интересный пример. Давайте допустим, что у нас есть большая труба, и к ней заварены две другие, но одна в два раза меньше диаметром, чем другая.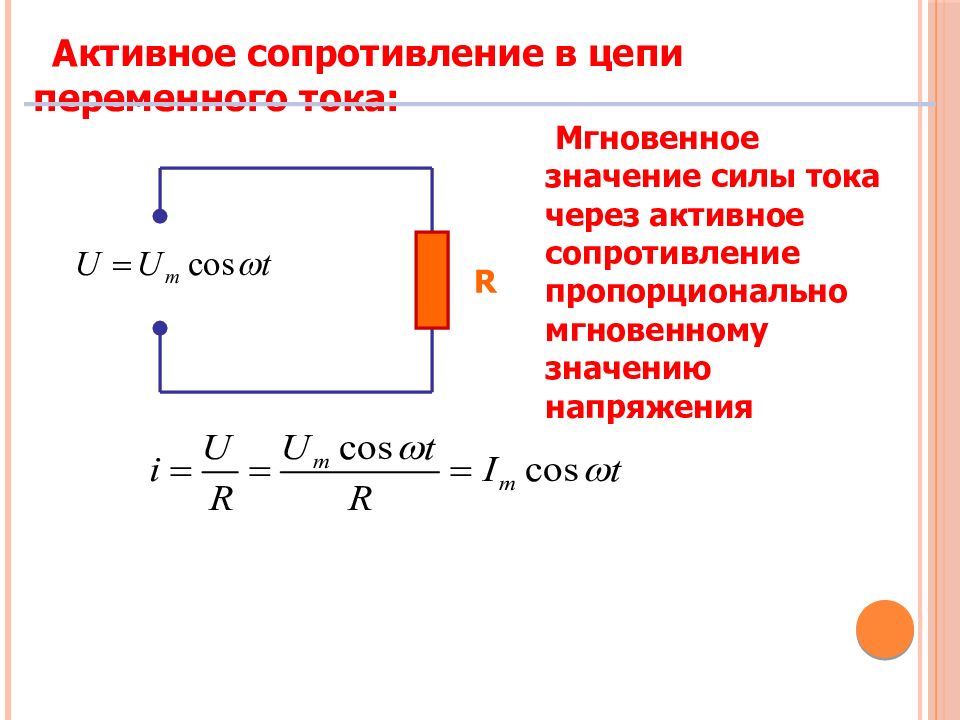
Из какой трубы объем воды будет выходить больше за секунду времени? Разумеется с той, которая толще в диаметре, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 малой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, который протекает через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.
Что такое сила тока?
Итак, теперь давайте все что мы тут пописали про водичку применим к электронике. Провод – это шланг. Тонкий провод – это тонкий в диаметре шланг, толстый провод – это толстый в диаметре шланг, можно сказать – труба. Молекулы воды – это электроны. Следовательно, толстый провод при одинаковом напряжении можно протащить больше электронов, чем тонкий. И вот здесь мы подходим вплотную к самой терминологии силы тока.
Сила тока – это количество электронов, прошедших через площадь поперечного сечения проводника за какое-либо определенное время.
Все это выглядит примерно вот так. Здесь я нарисовал круглый проводок, “разрезал” его и получил ту самую площадь поперечного сечения. Именно через нее и бегут электроны.
За период времени берут 1 секунду.
Формула силы тока
Формула для чайников будет выглядеть вот так:
где
I – собственно сила тока, Амперы
N – количество электронов
t – период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:
где
Δq – это заряд за какой-то определенный промежуток времени, Кулон
Δt – тот самый промежуток времени, секунды
I – сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10-19 Кулон.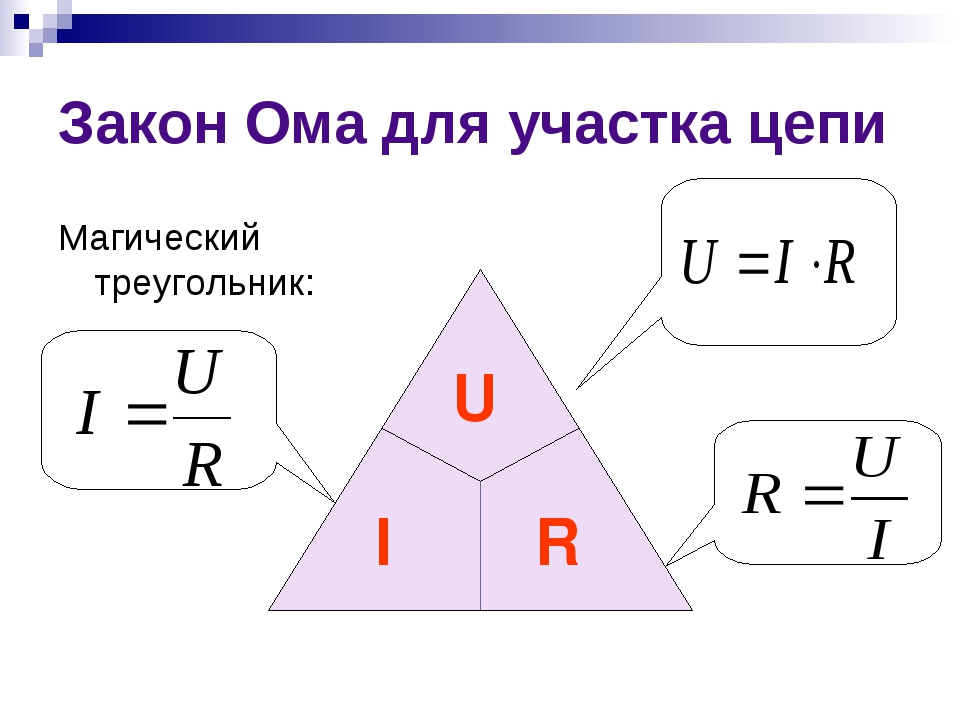 Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока – это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время. Измеряется как Кулон/секунда. Чтобы сэкономить время и по другим морально-эстетическим нормам, Кулон/секунду договорились называть Ампером, в честь французского ученого-физика.
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет “протащить” через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его “порвет”, то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
плавкий предохранитель
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
сгоревший плавкий предохранитель
Поэтому, силовые кабели, через которые “бегут” сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
Очень часто можно увидеть задачки по физике с вопросом: какая сила тока в проводнике? Проводник, он же провод, может иметь различные параметры: диаметр, он же площадь поперечного сечения; материал, из которого сделан провод; длина, которая играет также важную роль.
Да и вообще, сопротивление проводника рассчитывается по формуле:
формула сопротивления проводника
Таблица с удельным сопротивлением из разных материалов выглядит вот так.
таблица с удельным сопротивлением веществ
Для того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:
закон Ома
Задача
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?
задача на силу тока в проводнике
Решение:
Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы – амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.
Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое “сила тока”.
Закон Ома.
Закон Ома.
Программа КИП и А
В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..
Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I — сила тока, измеряемая в Амперах, (A) |
| U — напряжение, измеряемое в Вольтах, (V) | ||
| R — сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P — эл. мощность, измеряемая в Ваттах, (W) |
| I — сила тока, измеряемая в Амперах, (A) | ||
| U — напряжение, измеряемое в Вольтах, (V) |
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока. | |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I — сила переменного тока, измеряемая в Амперах, (A) |
| U — напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z — полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Вычислить эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторы
серии
Считается, что резисторы
включены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Рисунок \ (\ PageIndex {3} \): Простая последовательная схема с пятью резисторами.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {ряд эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от аккумулятора, некоторые проходят через резистор \ (R_1 \), а некоторые — через резистор \ (R_2 \).Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. \ nonumber \]
Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе. На рисунке \ (\ PageIndex {4} \) правило соединения дает \ (I = I_1 + I_2 \). В этой схеме есть два контура, которые приводят к уравнениям \ (V = I_1R_1 \) и \ (I_1R_1 = I_2R_2 \). Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (\ (V = V_1 = V_2 \)), а ток — аддитивный:
\ [\ begin {align *} I & = I_1 + I_2 \\ [4pt] & = \ frac {V_1} {R_1} + \ frac {V_2} {R_2} \\ [4pt] & = \ frac {V } {R_1} + \ frac {V} {R_2} \\ [4pt] & = V \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) = \ frac {V} {R_ {P}} \ end {align *} \]
Решение для \ (R_ {P} \)
\ [R_ {P} = \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) ^ {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет равен \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельное соединение. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая горизонтально с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.
Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса — включить резисторы в качестве индексов. Здесь эквивалентное сопротивление \ (R_3 \) и \ (R_4 \) равно
.
\ [R_ {34} = R_3 + R_4 = 6 \, \ Omega + 4 \, \ Omega = 10 \, \ Omega. \ nonumber \]
Схема теперь сокращается до трех резисторов, как показано на рисунке \ (\ PageIndex {5c} \). Перерисовывая, мы теперь видим, что резисторы \ (R_2 \) и \ (R_ {34} \) составляют параллельную цепь. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать в параллельной комбинации \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.
\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какую мощность рассеивает \ (R_2 \)?
Рисунок \ (\ PageIndex {6} \): Эти три резистора подключены к источнику напряжения так, чтобы \ (R_2 \) и \ (R_3 \) были параллельны друг другу, и эта комбинация была последовательно с \ (R_1 \).
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаково: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Решение
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и проявляться в виде тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.
Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
- Нарисуйте четкую принципиальную схему (рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, обеспечиваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного подключения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Закон Ома
| Клуб электроники
Закон Ома | Клуб электроники
Следующая страница: Power and Energy
См. Также: Напряжение и ток | Сопротивление
Закон Ома показывает взаимосвязь между напряжением, током и сопротивлением
Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между тремя величинами: напряжением, током и сопротивлением.
Закон Ома можно записать в виде словесного уравнения :
напряжение = ток × сопротивление Или используя символы для обозначения величин напряжения (В), тока (I) и сопротивления (R):
На самом деле это можно записать тремя способами, и вы можете выбрать версию, которая лучше всего подходит для ваших целей:
Треугольник ВИР — способ запомнить закон Ома
Вы можете использовать треугольник ВИР, чтобы помочь вам запомнить три версии закона Ома.
- Для расчета напряжения, В : поместите палец на V,
это оставляет I R, поэтому уравнение V = I × R - Чтобы рассчитать ток , I : положите палец на I,
это оставляет V над R, поэтому уравнение I = V / R - Для расчета сопротивления R : поместите палец на R,
это оставляет V над I, поэтому уравнение R = V / I
Расчет по закону Ома
Используйте этот метод для проведения расчетов:
- Запишите значения , при необходимости конвертируя единицы.
- Выберите необходимое Equation (используйте треугольник VIR).
- Введите числа в уравнение и вычислите ответ.
Должно быть V ery E asy N ow!
См. Примеры ниже:Пример 3:
Резистор 1,2 кОм пропускает ток 0,2 А, какое напряжение на нем?
Пример 4:
9 В подается на резистор 15 кОм, какой ток?
- В значений: V = 9V, I =?, R = 15k
- E предложение: I = V / R
- N единиц: Ток, I = 9 / 15 = 0.6 мА
(использование k для сопротивления означает, что расчет дает ток в мА)
Следующая страница: Энергетика | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.
На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.Рекламодателям не передается никакая личная информация.
Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
клуб электроники.инфо © Джон Хьюс 2021
Закон
Ома — Как соотносятся напряжение, ток и сопротивление | Закон Ома
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться.Это непрерывное движение электрического заряда через проводники цепи называется током , и его часто называют «потоком», как поток жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» в цепи, называется напряжением . Напряжение — это особая мера потенциальной энергии, которая всегда относительна между двумя точками.
Когда мы говорим об определенном количестве напряжения, присутствующем в цепи, мы имеем в виду измерение того, сколько потенциальной энергии существует для перемещения носителей заряда из одной конкретной точки в этой цепи в другую конкретную точку.Без ссылки на два конкретных пункта термин «напряжение» не имеет значения.
Ток имеет тенденцию проходить через проводники с некоторой степенью трения или сопротивления движению. Это противодействие движению правильнее называть сопротивлением . Сила тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующей прохождению тока.
Как и напряжение, сопротивление — это величина, относительная между двумя точками.По этой причине величины напряжения и сопротивления часто указываются как «между» или «поперек» двух точек в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, мы должны уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любой другой вид физической величины. Для массы мы можем использовать единицы «килограмм» или «грамм».
Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия.Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
«Символ», присвоенный каждой величине, представляет собой стандартную буквенную букву, используемую для представления этой величины в алгебраическом уравнении. Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.
«Аббревиатура единицы» для каждой величины представляет собой алфавитный символ, используемый в качестве сокращенного обозначения для конкретной единицы измерения.И да, этот странно выглядящий символ «подкова» — это заглавная греческая буква Ω, просто символ иностранного алфавита (извинения перед читателями-греками).
Каждая единица измерения названа в честь известного экспериментатора в области электричества: усилитель в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта и Ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение.«R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна представлять «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые споры по поводу значения слова «я».
Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах зарезервировано «E» для обозначения напряжения на источнике (таком как батарея или генератор) и «V» для обозначения напряжения на чем-либо еще.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (называемого «мгновенным» значением). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», в то время как пик напряжения при ударе молнии в тот самый момент, когда он попадает в линию электропередачи, скорее всего, будет обозначается строчной буквой «е» (или строчной буквой «v»), чтобы обозначить это значение как имеющееся в один момент времени.
То же самое соглашение о нижнем регистре справедливо и для тока, строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Кулон и электрический заряд
Одна из основных единиц измерения электрического тока, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, — это единица кулона , которая представляет собой меру электрического заряда, пропорционального количеству электронов в несбалансированном состоянии.Один кулон заряда равен 6 250 000 000 000 000 000 электронов.
Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается заглавной буквой «C». Бывает так, что единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этих терминах ток — это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение является мерой потенциальной энергии на единицу заряда , доступной для стимулирования прохождения тока из одной точки в другую.Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида — джоуль , что равняется количеству работы, совершаемой силой в 1 ньютон, возникающей при движении на 1 метр (в том же направлении).
В британских подразделениях это чуть меньше 3/4 фунта силы, приложенной на расстоянии 1 фута. Проще говоря, требуется около 1 джоуля энергии, чтобы поднять гирю весом 3/4 фунта на 1 фут от земли или перетащить что-то на расстояние 1 фут, используя параллельную тяговую силу 3/4 фунта.В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Уравнение закона Ома
Принципиальное открытие
Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, прямо пропорциональна напряжению, приложенному к нему при любой заданной температуре.Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя методы алгебры, мы можем преобразовать это уравнение в два варианта, решая для I и R соответственно:
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа).Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы рассчитаем величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Какой ток (I) в этой цепи?
В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Какое сопротивление (R) дает лампа?
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Какое напряжение обеспечивает аккумулятор?
Техника треугольника закона Ома
Закон Ома — очень простой и полезный инструмент для анализа электрических цепей.Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, позволяющая вспомнить, как решить для любого количества, учитывая два других.
Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
В конце концов, вам придется быть знакомым с алгеброй, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений.Если вы знакомы с алгеброй, все, что вам нужно сделать, это зафиксировать E = IR в памяти и вывести из нее две другие формулы, когда они вам понадобятся!
ОБЗОР:
- Напряжение измеряется в вольтах , обозначается буквами «E» или «V».
- Ток измеряется в амперах , обозначается буквой «I».
- Сопротивление измеряется в Ом. обозначается буквой «R».
- Закон Ома: E = IR; I = E / R; R = E / I
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
Оценка внутреннего сопротивления в цепях | Электрические схемы
Рабочий пример 7: Внутреннее сопротивление в цепи с последовательно включенными резисторами
Для следующей схемы рассчитайте:
разности потенциалов \ (V_ \ text {1} \), \ (V_ \ text {2} \) и \ (V_ \ text {3} \) на резисторах \ (R_ \ text {1} \), \ (R_ \ text {2} \) и \ (R_ \ text {3} \)
.
сопротивление \ (R_ \ text {3} \).
сопротивление \ (R_ \ text {3} \).
Если внутреннее сопротивление равно \ (\ text {0,1} \) \ (\ text {Ω} \), какова ЭДС батареи и какая мощность рассеивается внутренним сопротивлением батареи?
Примечание
Это вопрос, очень похожий на то, что вы видели ранее. Это необходимо для того, чтобы выделить
Дело в том, что подход к внутреннему сопротивлению строится на том же
принципы, с которыми вы уже работали.Определите, как подойти к проблеме
Нам дана разность потенциалов на ячейке и ток в цепи, а также сопротивления двух из трех резисторов.Мы можем использовать закон Ома для расчета разности потенциалов на известных резисторах. Поскольку резисторы включены в последовательную цепь, разность потенциалов равна \ (V = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \), и мы можем вычислить \ (V_ \ text {3} \). Теперь мы можем использовать эту информацию, чтобы найти разность потенциалов на неизвестном резисторе \ (R_ \ text {3} \).
Вычислить разность потенциалов на \ (R_ \ text {1} \)
Используя закон Ома:
\ begin {align *}
R_ \ text {1} & = \ frac {V_ \ text {1}} {I} \\
I \ cdot R_ \ text {1} & = I \ cdot \ frac {V_ \ text {1}} {I} \\
V_ \ text {1} & = {I} \ cdot {R_ \ text {1}} \\
& = 2 \ cdot 1 \\
V_ \ текст {1} & = \ текст {2} \ текст {V}
\ end {align *}Вычислить разность потенциалов на \ (R_ \ text {2} \)
Снова используя закон Ома:
\ begin {align *}
R_ \ text {2} & = \ frac {V_ \ text {2}} {I} \\
I \ cdot R_ \ text {2} & = I \ cdot \ frac {V_ \ text {2}} {I} \\
V_ \ text {2} & = {I} \ cdot {R_ \ text {2}} \\
& = 2 \ cdot 3 \\
V_ \ текст {2} & = \ текст {6} \ текст {V}
\ end {align *}Вычислить разность потенциалов на \ (R_ \ text {3} \)
Поскольку разность потенциалов на всех резисторах, вместе взятых, должна быть такой же, как разность потенциалов на ячейке в последовательной цепи, мы можем найти \ (V_ \ text {3} \), используя:
\ begin {align *}
V & = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \\
V_ \ text {3} & = V — V_ \ text {1} — V_ \ text {2} \\
& = 23-2-6 \\
V_ \ текст {3} & = \ текст {15} \ текст {V}
\ end {align *}Найдите сопротивление \ (R_ \ text {3} \)
Нам известна разность потенциалов на \ (R_ \ text {3} \) и ток через нее, поэтому мы можем использовать закон Ома для вычисления значения сопротивления:
\ begin {align *}
R_ \ text {3} & = \ frac {V_ \ text {3}} {I} \\
& = \ frac {\ text {15}} {\ text {2}} \\
R_ \ text {3} & = \ text {7,5} ~ \ Omega
\ end {align *}Разница потенциалов на внутреннем сопротивлении батареи
Значение ЭДС можно рассчитать по разности потенциалов нагрузки и разности потенциалов на внутреннем сопротивлении.2} {R} \), и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов в ней, поэтому мы можем использовать любую форму уравнения для мощности:
\ begin {align *}
P_r & = V_rI_r \\
& = (\ текст {0,2}) (\ текст {2}) \\
& = \ текст {0,4} \ текст {W}
\ end {align *}Напишите окончательный ответ
- \ (V_ \ text {1} = \ text {2,0} \ text {V} \)
- \ (V_ \ text {2} = \ text {6,0} \ text {V} \)
- \ (V_ \ text {3} = \ text {10,0} \ text {V} \)
- \ (R_ \ text {3} = \ text {7,5} \ Omega \)
- \ (\ mathcal {E} = \ text {23,2} \ text {V} \)
- \ (P_r = \ text {0,4} \ text {W} \)
Рабочий пример 8: Внутреннее сопротивление и резисторы параллельно
Разность потенциалов на батарее составляет 18 В, когда она подключена к двум параллельным резисторам \ (\ text {4,00} \) \ (\ Omega \) и \ (\ text {12,00} \) \ ( \ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов. Если внутреннее сопротивление батареи \ (\ text {0,375} \) \ (\ text {Ω} \), какова ЭДС батареи?
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи. Резисторы включены параллельно и поэтому:
\ begin {align *}
\ frac {\ text {1}} {R} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2}} \ \
& = \ frac {\ text {1}} {\ text {4}} + \ frac {\ text {1}} {\ text {12}} \\
& = \ frac {3 + 1} {\ text {12}} \\
& = \ frac {\ text {4}} {\ text {12}} \\
R & = \ frac {\ text {12}} {\ text {4}} = \ text {3,00} \ \ Omega
\ end {выровнять *}
Теперь, используя закон Ома, чтобы найти ток через ячейку:
\ begin {align *}
R & = \ frac {V} {I} \\
I & = \ frac {V} {R} \\
& = \ frac {\ text {18}} {\ text {3}} \\
I & = \ text {6,00} \ text {A}
\ end {align *}Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной конфигурации резисторов разность потенциалов на ячейке такая же, как и разность потенциалов на каждом из параллельных резисторов.Для этой схемы:
\ begin {align *}
V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с вычисления тока через \ (R_ \ text {1} \) по закону Ома:
\ begin {align *}
R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\
I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\
& = \ frac {\ text {18}} {\ text {4}} \\
I_ \ text {1} & = \ text {4,50} \ text {A}
\ end {align *}Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_ \ text {2} \):
\ begin {align *}
R_ \ text {2} & = \ frac {V_ \ text {2}} {I_ \ text {2}} \\
I_ \ text {2} & = \ frac {V_ \ text {2}} {R_ \ text {2}} \\
& = \ frac {\ text {18}} {\ text {12}} \\
I_ \ text {2} & = \ text {1,50} \ text {A}
\ end {выровнять *}Альтернативный метод вычисления \ (I_ \ text {2} \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять общий ток через ячейку:
\ begin {align *}
I & = I_ \ text {1} + I_ \ text {2} \\
I_ \ text {2} & = I — I_ \ text {1} \\
& = 6 — 4.5 \\
I_ \ text {2} & = \ text {1,5} \ text {A}
\ end {align *}Определить ЭДС
Суммарный ток через батарею — это ток через внутреннее сопротивление батареи. Знание силы тока и сопротивления позволяет нам использовать закон Ома для определения разности потенциалов на внутреннем сопротивлении и, следовательно, ЭДС батареи.
Используя закон Ома, мы можем определить разность потенциалов на внутреннем сопротивлении:
\ begin {align *}
V & = I \ cdot r \\
& = \ текст {6} \ cdot \ text {0,375} \\
& = \ текст {2,25} \ текст {V}
\ end {выровнять *}Мы знаем, что ЭДС аккумулятора — это разность потенциалов на выводе, суммированная с разностью потенциалов на внутреннем сопротивлении, так:
\ begin {align *}
\ mathcal {E} & = V + Ir \\
& = \ text {18} + \ text {2,25} \\
& = \ текст {20,25} \ текст {V}
\ end {align *}Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6,00} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4,00} \) \ (\ Omega \) равен \ (\ text {4,50} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12,00} \) \ (\ Omega \) равен \ (\ text {1,50} \) \ (\ text {A} \).
ЭДС аккумулятора равна \ (\ text {20,25} \) \ (\ text {V} \).
Рабочий пример 9: Мощность в последовательной и параллельной сетях резисторов
Учитывая следующую схему:
Ток, покидающий батарею, равен \ (\ text {1,07} \) \ (\ text {A} \), общая мощность, рассеиваемая во внешней цепи, равна \ (\ text {6,42} \) \ ( \ text {W} \), отношение полных сопротивлений двух параллельных сетей \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, соотношение \ (R_ \ text {1}: R_ \ text {2} \) равно 3: 5 и \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \).
Определите:
- разность потенциалов АКБ,
- мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \), и
- , если батарея имеет ЭДС, равную \ (\ text {6,50} \) \ (\ text {V} \), каково значение сопротивления каждого резистора и мощность, рассеиваемая в каждом из них.
Что требуется
В этом вопросе вам дается различная информация и предлагается определить мощность, рассеиваемую каждым резистором и каждой комбинацией резисторов.Обратите внимание, что данная информация в основном относится ко всей цепи. Это подсказка, которую вы должны начать с общей схемы и двигаться вниз к более конкретным элементам схемы.
Расчет разности потенциалов аккумулятора
В первую очередь остановимся на батарее. Нам дана мощность всей цепи, а также ток, выходящий из батареи. Мы знаем, что разность потенциалов на клеммах аккумулятора — это разность потенциалов в цепи в целом.
Мы можем использовать соотношение \ (P = VI \) для всей схемы, потому что разность потенциалов такая же, как разность потенциалов на клеммах батареи:
\ begin {align *}
P & = VI \\
V & = \ frac {P} {I} \\
& = \ frac {\ text {6,42}} {\ text {1,07}} \\
& = \ текст {6,00} \ текст {V}
\ end {align *}Разность потенциалов на батарее равна \ (\ text {6,00} \) \ (\ text {V} \).
Мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \)
Помните, что мы работаем от общих деталей схемы вниз к деталям отдельных элементов, это противоположно тому, как вы относились к этой схеме ранее.
Мы можем рассматривать параллельные сети как эквивалентные резисторы, поэтому схема, с которой мы сейчас работаем, выглядит так:
Мы знаем, что ток через два элемента схемы будет одинаковым, потому что это последовательная цепь и что сопротивление всей цепи должно быть: \ (R_ {Ext} = R_ {P \ text {1}} + R_ {P \ text {2}} \). Мы можем определить полное сопротивление по закону Ома для цепи в целом:
\ begin {align *}
V_ {батарея} & = IR_ {Ext} \\
R_ {Ext} & = \ frac {V_ {аккумулятор}} {I} \\
& = \ frac {\ text {6,00}} {\ text {1,07}} \\
& = \ текст {5,61} \ текст {Ω}
\ end {align *}Мы знаем, что соотношение между \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, что означает, что мы знаем:
\ begin {align *}
R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \ \ \ text {и} \\
R_T & = R_ {P \ text {1}} + R_ {P \ text {2}} \\
& = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} + R_ {P \ text {2}} \\
& = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\
(\ text {5,61}) & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\
R_ {P \ text {2}} & = \ frac {\ text {2}} {\ text {3}} (\ text {5,61}) \\
R_ {P \ text {2}} & = \ text {3,74} \ text {Ω}
\ end {выровнять *}
и поэтому:
\ begin {align *}
R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \\
& = \ frac {\ text {1}} {\ text {2}} (3.2 (\ text {3,74}) \\
& = \ текст {4,28} \ текст {W}
\ end {выровнять *}
Эти значения будут в сумме с исходным значением мощности, которое у нас было для внешней цепи. Если бы они не
мы бы сделали ошибку в расчетах.Расчет параллельной сети 1
Теперь мы можем приступить к детальному расчету первого набора параллельных резисторов.
Мы знаем, что соотношение между \ (R _ {\ text {1}}: R _ {\ text {2}} \) составляет 3: 5, что означает, что мы знаем \ (R _ {\ text {1}} = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \).Нам также известно общее сопротивление двух параллельных резисторов в этой сети.
это \ (\ text {1,87} \) \ (\ text {Ω} \). Мы можем использовать
соотношение между значениями двух резисторов, а также формула для общей
сопротивление (\ (\ frac {\ text {1}} {R_PT} = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2 }} \))
чтобы найти номиналы резисторов:
\ begin {align *}
\ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} { R_ \ text {2}} \\
\ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {5}} {3R_ \ text {2}} + \ frac {\ text {1}} { R_ \ text {2}} \\
\ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + 1) \\
\ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + \ frac {\ text {3}} {\ text {3}}) \\
\ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} \ frac {\ text {8}} {\ текст {3}} \\
R_ \ text {2} & = R_ {P \ text {1}} \ frac {\ text {8}} {\ text {3}} \\
& = (\ text {1,87}) \ frac {\ text {8}} {\ text {3}} \\
& = \ текст {4,99} \ текст {Ω}
\ end {выровнять *}
Мы также можем вычислить \ (R _ {\ text {1}} \):
\ begin {align *}
R _ {\ text {1}} & = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \\
& = \ frac {\ text {3}} {\ text {5}} (\ text {4,99}) \\
& = \ текст {2,99} \ текст {Ω}
\ end {align *}Для определения мощности нам нужно рассчитанное нами сопротивление и либо разность потенциалов, либо ток.Два резистора включены параллельно, поэтому разность потенциалов между ними такая же, как и разность потенциалов в параллельной сети. Мы можем использовать закон Ома для определения разности потенциалов в сети параллельных резисторов, поскольку мы знаем общее сопротивление и ток:
\ begin {align *}
V & = I R \\
& = (\ text {1,07}) (\ text {1,87}) \\
& = \ текст {2,00} \ текст {V}
\ end {align *}Теперь у нас есть информация, необходимая для определения мощности через каждый резистор:
\ begin {align *}
P_ \ text {1} & = \ frac {V ^ 2} {R_ \ text {1}} \\
& = \ frac {(\ text {2,00}) ^ 2} {\ text {2,99}} \\
& = \ текст {1,34} \ текст {W}
\ end {выровнять *}\ begin {align *}
P_ \ text {2} & = \ frac {V ^ 2} {R_ \ text {2}} \\
& = \ frac {(\ text {2,00}) ^ 2} {\ text {4,99}} \\
& = \ текст {0,80} \ текст {W}
\ end {align *}Параллельная сеть 2 расчета
Теперь мы можем приступить к детальному расчету второго набора параллельных резисторов.
Нам дано \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \), и мы знаем \ (R_ {P \ text {2}} \), поэтому мы можем вычислить \ (R_ \ text {4} \) из:
\ begin {align *}
\ frac {\ text {1}} {R_ {P \ text {2}}} & = \ frac {\ text {1}} {R_ \ text {3}} + \ frac {\ text {1}} { R_ \ text {4}} \\
\ frac {\ text {1}} {\ text {3,74}} & = \ frac {\ text {1}} {\ text {7,00}} + \ frac {\ text {1}} {R_ \ текст {4}} \\
R_ \ text {4} & = \ text {8,03} \ text {Ω}
\ end {align *}Мы можем вычислить разность потенциалов во второй параллельной сети, вычтя разность потенциалов первой параллельной сети из разности потенциалов батареи, \ (V_ {P \ text {2}} = \ text {6,00} — \ text {2,00} = \ text {4,00} \ text {V} \).2} {\ text {8,03}} \\
& = \ текст {1,99} \ текст {W}
\ end {align *}Внутреннее сопротивление
Мы знаем, что ЭДС батареи равна \ (\ text {6,5} \) \ (\ text {V} \), но что разность потенциалов, измеренная на клеммах, составляет всего \ (\ text {6} \) \ (\ текст {V} \). Разница — это разность потенциалов на внутреннем сопротивлении батареи, и мы можем использовать известный ток и закон Ома для определения внутреннего сопротивления:
\ begin {align *}
V & = I \ cdot R \\
R & = \ frac {V} {I} \\
& = \ frac {\ text {0,5}} {\ text {1,07}} \\
& = \ text {0,4672897} \\
& = \ текст {0,47} \ текст {Ω}
\ end {выровнять *}Мощность, рассеиваемая внутренним сопротивлением батареи:
\ begin {align *}
P & = VI \\
& = \ текст {0,5} \ cdot \ text {1,07} \\
& = \ текст {0,535} \ текст {W}
\ end {align *}Рабочий пример 10: Внутреннее сопротивление и фары [NSC 2011 Paper 1]
Фара и два ИДЕНТИЧНЫХ задних фонаря скутера подключены параллельно к батарее с неизвестным внутренним сопротивлением, как показано на упрощенной принципиальной схеме ниже.Фара имеет сопротивление \ (\ text {2,4} \) \ (\ text {Ω} \) и управляется переключателем \ (\ textbf {S} _1 \). Задние фонари управляются переключателем \ (\ textbf {S} _2 \). Сопротивлением соединительных проводов можно пренебречь.
График рядом показывает разность потенциалов на клеммах батареи до и после включения переключателя \ (\ textbf {S} _1 \) (пока переключатель \ (\ textbf {S} _2 \) открыт). Переключатель \ (\ textbf {S} _1 \) закрывается в момент \ (\ textbf {t} _1 \).
Используйте график, чтобы определить ЭДС аккумулятора.
(1 балл)
ПРИ ТОЛЬКО ВЫКЛЮЧАТЕЛЬ \ (\ textbf {S} _1 \) ЗАКРЫТО, рассчитайте следующее:
Ток через фару
(3 балла)
Внутреннее сопротивление \ (r \) батареи
(3 балла)
ОБЕ ПЕРЕКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) ТЕПЕРЬ ЗАКРЫТЫ.В течение этого периода аккумулятор обеспечивает ток \ (\ text {6} \) \ (\ text {A} \).
Рассчитайте сопротивление каждого заднего фонаря.
(5 баллов)
Как повлияет на показания вольтметра, если фара перегорит? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) все еще закрыты.)
Запишите только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ОДИН ТО ЖЕ.
Дайте объяснение.
(3 балла)
Вопрос 1
\ (\ text {12} \) \ (\ text {V} \)
(1 балл)
Вопрос 2.1
Вариант 1:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {9,6}} {\ text {2,4}} \\
& = \ текст {4 A}
\ end {выровнять *}Вариант 2:
\ begin {align *}
\ text {emf} & = IR + Ir \\
12 & = I (\ text {2,4}) + \ text {2,4} \\
\ поэтому I & = \ text {4 A}
\ end {выровнять *}(3 балла)
Вопрос 2.2
Вариант 1:
\ begin {align *}
\ text {emf} & = IR + Ir \\
12 & = \ text {9,4} + 4r \\
r & = \ текст {0,6} \ \ Omega
\ end {выровнять *}Вариант 2:
\ begin {align *}
V_ {потеряно} & = Ir \\
\ text {2,4} & = \ text {4} r \\
\ поэтому r & = \ text {0,6} \ \ Omega
\ end {выровнять *}Вариант 3:
\ begin {align *}
\ text {emf} & = I (R + r) \\
\ text {12} & = \ text {4} (\ text {2,4} + r) \\
\ поэтому r & = \ text {0,6} \ \ Omega
\ end {выровнять *}(3 балла)
Вопрос 3
Вариант 1:
\ begin {align *}
\ text {emf} & = IR + Ir \\
\ text {12} & = \ text {6} (R + \ text {0,6}) \\
R _ {\ text {ext}} & = \ text {1,4} \ \ Omega
\ end {align *} \ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\
R & = \ текст {3,36} \ \ Omega
\ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 2:
\ begin {align *}
\ text {Emf} & = V _ {\ text {terminal}} + Ir \\
12 & = V _ {\ text {терминал}} + 6 (\ text {0,6}) \\
\ поэтому V _ {\ text {terminal}} & = \ text {8,4} \ text {V}
\ end {align *} \ begin {align *}
I _ {\ text {2,4} \ \ Omega} & = \ frac {V} {R} \\
& = \ frac {\ text {8,4}} {\ text {2,4}} \\
& = \ text {3,5 A}
\ end {align *} \ begin {align *}
I _ {\ text {задние фонари}} & = 6 — \ text {3,5} \\
& = \ текст {2,5} \ текст {A} \\
R _ {\ text {задние фонари}} & = \ frac {V} {I} \\
& = \ frac {\ text {8,4}} {\ text {2,5}} \\
& = \ текст {3,36} \ \ Omega \\
R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega
\ end {выровнять *}Вариант 3:
\ begin {align *}
V & = IR \\
\ text {12} & = \ text {6} (R) \\
R _ {\ text {ext}} & = 2 \ \ Omega
\ end {align *} \ begin {align *}
R _ {\ text {parallel}} & = 2 — \ text {0,6} \\
& = \ текст {1,4} \ \ Omega \\
\ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\
R & = \ текст {3,36} \ \ Omega
\ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 4:
Для параллельной комбинации: \ (I_ {1} + I_ {2} = 6 \ text {A} \)
\ begin {align *}
\ поэтому \ frac {V} {\ text {2,4}} + \ frac {V} {R _ {\ text {задние фонари}}} & = \ text {6} \\
\ text {8,4} \ left (\ frac {1} {\ text {2,4}} + \ frac {1} {R _ {\ text {задние фонари}}} \ right) & = \ text {6 } \\
\ поэтому R _ {\ text {задние фонари}} & = \ text {3,36} \ \ Omega \\
R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega
\ end {выровнять *}(5 баллов)
Вопрос 4
Увеличивается
Сопротивление увеличивается, а ток уменьшается.Таким образом, \ (Ir \) (потерянное вольт) должно уменьшаться, что приводит к увеличению напряжения.
(3 балла)
[ИТОГО: 15 баллов]
Как рассчитать силу тока в последовательной цепи
Обновлено 28 декабря 2020 г.
Автор S. Hussain Ather
Цепи серии
соединяют резисторы таким образом, что ток, измеряемый по амплитуде или силе тока, проходит по одному пути в цепи и остается постоянным на всем протяжении . Ток протекает в противоположном направлении электронов через каждый резистор, которые препятствуют потоку электронов, один за другим в одном направлении от положительного конца батареи к отрицательному.Нет внешних ветвей или путей, по которым может проходить ток, как в параллельной цепи.
Примеры цепей серии
Цепи последовательной передачи широко используются в повседневной жизни. Примеры включают некоторые типы рождественских или праздничных огней. Другой распространенный пример — выключатель света. Кроме того, компьютеры, телевизоры и другие бытовые электронные устройства работают по концепции последовательной цепи.
Сила тока (или Ампер) в последовательной цепи
Вы можете рассчитать амплитуду в амперах или амперах, задаваемую переменной A, последовательной цепи, суммируя сопротивление на каждом резисторе в цепи как R и суммируя падения напряжения как В , затем решая I в уравнении V = I / R , в котором V — напряжение батареи в вольтах, I — это ток, а R — полное сопротивление резисторов в омах (Ом).Падение напряжения должно быть равно напряжению батареи в последовательной цепи.
Уравнение V = I / R , известное как закон Ома, также справедливо для каждого резистора в цепи. Ток в последовательной цепи постоянный, что означает, что он одинаков на каждом резисторе. Вы можете рассчитать падение напряжения на каждом резисторе, используя закон Ома. При последовательном включении напряжение батарей увеличивается, что означает, что они служат меньше времени, чем если бы они были подключены параллельно.
Последовательная принципиальная схема и формула
••• Syed Hussain Ather
В приведенной выше схеме каждый резистор (обозначенный зигзагообразными линиями) подключен к источнику напряжения, батарее (обозначенной + и — окружающие отключенные линии), последовательно. Ток течет в одном направлении и остается постоянным в каждой части цепи.
Если вы просуммируете каждый резистор, вы получите полное сопротивление 18 Ом (Ом, где Ом — это мера сопротивления).{-t / (RC)}
, в котором V — в вольтах, R — в омах, C — в фарадах, t — время в секундах и I в амперах. Здесь e относится к постоянной Эйлера e .
Общая емкость последовательной цепи равна
\ frac {1} {C_ {total}} = \ frac {1} {C_1} + \ frac {1} {C_2} + …
дюйм каждая инверсия каждого отдельного конденсатора суммируется с правой стороны ( 1 / C 1 , 1 / C 2 и т. д.{-tR / L}
, в котором общая индуктивность L является суммой значений индуктивностей отдельных катушек индуктивности, измеренных в единицах Генри. Когда последовательная цепь накапливает заряд при протекании тока, катушка индуктивности, которая обычно окружает магнитный сердечник, генерирует магнитное поле в ответ на протекание тока. Их можно использовать в фильтрах и генераторах. Сравнение последовательностей
и параллельных цепей
При работе с параллельными цепями, в которых ток разветвляется через разные части цепей, вычисления «меняются местами».”Вместо определения общего сопротивления как суммы отдельных сопротивлений, общее сопротивление определяется как
\ frac {1} {R_ {total}} = \ frac {1} {R_1} + \ frac {1} {R_2 } + …
(аналогично вычислению полной емкости последовательной цепи).
Напряжение, а не ток, постоянно во всей цепи. Общий ток параллельной цепи равен сумме токов в каждой ветви. Вы можете рассчитать как ток, так и напряжение, используя закон Ома ( В = I / R ).
••• Syed Hussain Ather
В приведенной выше параллельной схеме полное сопротивление определяется следующими четырьмя шагами:
- 1 / R всего = 1 / R1 + 1 / R2 + 1 / R3
- 1 / R всего = 1/1 Ω + 1/4 Ω + 1/5 Ω
- 1 / R всего = 20/20 Ω + 5/20 Ом + 4/20 Ом
- 1 / R всего = 29/20 Ом
- R всего = 20/29 Ом или около.69 Ом
В приведенном выше расчете обратите внимание, что вы можете перейти к шагу 5 из шага 4 только тогда, когда есть только один член слева ( 1 / R всего ) и только один член справа сторона (29/20 Ом).
Аналогично, общая емкость в параллельной цепи — это просто сумма каждого отдельного конденсатора, а общая индуктивность также дается обратной зависимостью ( 1 / L всего = 1 / L 1 + 1 / L 2 +… ).
Зависимость постоянного тока от переменного
В цепях ток может течь либо постоянно, как в случае постоянного тока (DC), либо колебаться волнообразно в цепях переменного тока (AC). В цепи переменного тока ток в цепи меняется с положительного на отрицательное.
Британский физик Майкл Фарадей продемонстрировал силу постоянного тока с помощью динамо-электрогенератора в 1832 году, но он не мог передавать его мощность на большие расстояния, а напряжения постоянного тока требовали сложных схем.
Когда сербско-американский физик Никола Тесла в 1887 году создал асинхронный двигатель, использующий переменный ток, он продемонстрировал, как он легко передается на большие расстояния и может преобразовываться между высокими и низкими значениями с помощью трансформаторов — устройства, используемого для изменения напряжения. Достаточно скоро, примерно на рубеже 20-го века, домашние хозяйства по всей Америке начали отказываться от постоянного тока в пользу переменного тока.
В настоящее время электронные устройства используют как переменный, так и постоянный ток, когда это необходимо. Постоянный ток используется с полупроводниками для небольших устройств, которые нужно только включать и выключать, например ноутбуков и сотовых телефонов.Напряжение переменного тока передается по длинным проводам, прежде чем преобразуется в постоянный ток с помощью выпрямителя или диода для питания таких приборов, как лампочки и батареи.
Ток и сопротивление
Электрические цепи с движущимися зарядами — обычное дело в нашем технологическом обществе. Ток, сопротивление и электродвижущая сила — понятия, необходимые для описания этих цепей.
Текущий
Ток (I) — это количество заряда за время, которое проходит через область, перпендикулярную потоку:
Ток измеряется в единицах СИ — амперах (A), и
.
Это определение тока может применяться к зарядам, движущимся в проводе, в электролитической ячейке или даже в ионизированных газах.
При визуализации заряда, протекающего по цепи, не с точностью представить, как электроны движутся очень быстро по цепи. Средняя скорость или дрейфовая скорость ( v b ) отдельных зарядов мала; электроны проводимости в медной проволоке движутся со скоростью 10 –4 м / с. Формула
, где q — заряд электрона, A — площадь поперечного сечения провода, а n — количество электронов проводимости на кубический метр.При такой скорости время прохождения 10 см составляет около 11 минут. Из опыта очевидно, что лампочка загорится не так долго после включения выключателя. Когда цепь замыкается, все распределение зарядов почти немедленно реагирует на электрическое поле и приводится в движение почти одновременно, даже если отдельные заряды движутся медленно.
Батарея обеспечивает напряжение (В) между своими выводами. Электрическое поле, созданное в проводе, подключенном к клеммам батареи, вызывает протекание тока, которое возникает, когда ток имеет полный проводящий путь от одного контакта батареи к другому — это называется схемой .По соглашению направление тока во внешней цепи (не в батарее) является направлением движения положительных зарядов. В металлах электроны являются движущимися зарядами, поэтому определение направления тока противоположно действительному течению отрицательных зарядов в проводе. (Примечание: электрические поля не обнаруживаются в проводниках со статическими зарядами, как показывает закон Гаусса, но электрические поля могут существовать в проводнике, когда заряды находятся в движении.)
Разность потенциалов между клеммами аккумулятора при отсутствии тока называется электродвижущей силой (ЭДС).Исторический термин ЭДС является неправильным, потому что он измеряется в вольтах, а не в единицах силы, но терминология все еще широко используется.
Сопротивление и удельное сопротивление
Экспериментальным путем было обнаружено, что ток в проводниках пропорционален напряжению. Константа пропорциональности — это сопротивление в цепи. Это соотношение называется законом Ома : V = IR . Сопротивление измеряется в омах ( Вт, ): ом равен 1 вольт / 1 ампер.
Сопротивление проводника зависит от его длины (l) , площади поперечного сечения (A) и его удельного сопротивления ( r ). Удельное сопротивление для конкретного проводника можно найти в таблице свойств материалов. Единица измерения удельного сопротивления — ом-метр. Сопротивление току в проводнике возникает из-за того, что потоку движущихся зарядов препятствует материал провода. Интуитивно понятно, что сопротивление должно увеличиваться с увеличением длины провода, быть обратно пропорциональным площади поперечного сечения (меньшее сопротивление для большей площади) и зависеть от материала провода.Соотношение между сопротивлением и удельным сопротивлением равно
.
Примечание : Резистор — это особый электронный компонент, единственная функция которого — сопротивление току. Сопротивление генерируется любым препятствующим током, например, лампочкой или нагревательным элементом.
Электроэнергия и энергия
На рисунке 1 показана простая схема батареи с проводами, соединяющими ее с лампочкой. Нить накала лампы представляет собой сопротивление, обозначенное в цепи как R рядом с символом сопротивления.Обозначение напряжения батареи — ε. Предположим, что сопротивление в соединительных проводах незначительно, так что лампочка фактически является единственным сопротивлением в цепи. Аккумулятор обеспечивает постоянную разность потенциалов, например, 6 вольт. Когда ток проходит через лампочку, заряды переходят от более высокого потенциала к более низкому с разницей в 6 вольт. Энергия преобразуется в свет и тепло с помощью нити накала лампы.
Рисунок 1
Простая схема с лампочкой в виде резистора R .
Норма расхода энергии равна мощности , задаваемой любым из трех выражений:
Мощность измеряется в ваттах (Вт):
Цепи серии
— базовое электричество
Три закона для последовательных цепей
Существует три основных соотношения, касающихся сопротивления, тока и напряжения для всех последовательных цепей. Важно, чтобы вы усвоили три основных закона для последовательных цепей.
Сопротивление
Когда отдельные сопротивления соединяются последовательно, они действуют так же, как одно большое комбинированное сопротивление. Поскольку существует только один путь для протекания тока в последовательной цепи, и поскольку каждый из резисторов находится в линии, чтобы действовать как противодействие этому протеканию тока, общее сопротивление представляет собой комбинированное сопротивление всех резисторов, установленных в линию.
Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений в цепи .
Rt = R1 + R2 + R3…
Используя эту формулу, вы обнаружите, что полное сопротивление цепи равно:
RT = 15 Ом + 5 Ом + 20 Ом = 40 Ом
Рисунок 16. Последовательная схема
Текущая
Поскольку существует только один путь для потока электронов в последовательной цепи, ток имеет одинаковую величину в любой точке цепи.
Общий ток в последовательной цепи такой же, как ток через любое сопротивление цепи.
IT = I1 = I2 = I3…
Учитывая 120 В как общее напряжение и определив общее сопротивление цепи как 40 Ом, теперь вы можете применить закон Ома для определения полного тока в этой цепи:
IT = 120 В / 40 Ом = 3 А
Этот общий ток цепи останется неизменным для всех отдельных резисторов цепи.
Напряжение
Прежде чем ток пройдет через сопротивление, должна быть доступна разность потенциалов или напряжение. Когда резисторы соединены последовательно, они должны «делить» общее напряжение источника.
Общее напряжение в последовательной цепи равно сумме всех индивидуальных падений напряжения в цепи.
Когда ток проходит через каждый резистор в последовательной цепи, он устанавливает разность потенциалов на каждом отдельном сопротивлении.Это обычно называется падением напряжения, и его величина прямо пропорциональна величине сопротивления. Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.
ET = E1 + E2 + E3…
Используя закон Ома, вы можете определить напряжение на каждом резисторе.
3 А × 15 Ом = 45 В
3 А × 5 Ом = 15 В
3 А × 20 Ом = 60 В
Общее напряжение источника равно сумме отдельных падений напряжения:
45 В + 15 В + 60 В = 120 В
Обрыв в последовательной цепи
При появлении обрыва ток в цепи прерывается.Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю. Однако разность потенциалов источника очевидна. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.
Рисунок 17. Обрыв цепи
Влияние обрыва линии и потери линии
Медь и алюминий используются в качестве проводников, потому что они мало препятствуют прохождению тока.Хотя сопротивлением часто пренебрегают при простом анализе цепей, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.
Отказ от линии
Рисунок 18. Падение напряжения
Когда ток 10 А протекает через каждую линию с сопротивлением 0,15 Ом, на каждой линии появляется небольшое падение напряжения. Это падение напряжения на линейных проводниках обычно обозначается как падение линии .
Поскольку есть две линии, общее падение составляет 2 × 1.5 В = 3 В. Напряжение сети на нагрузке (117 В) меньше напряжения источника.
В некоторых ситуациях может потребоваться использование более крупных проводов с меньшим сопротивлением, чтобы падение напряжения в линии не слишком сильно уменьшало напряжение нагрузки.
Потеря линии
Другой термин, связанный с проводниками, — потери в линии. Это потеря мощности, выраженная в ваттах, и связана с рассеянием тепловой энергии, когда ток течет через сопротивление проводов линии.Потери в линии рассчитываются с использованием одного из уравнений мощности.
Используя предыдущий пример:
P = I 2 × R
P = (10A) 2 × 0,3 Ом
P = 30 Вт
* Помните:
- Падение напряжения в линии выражается в вольтах.


