Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .
Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).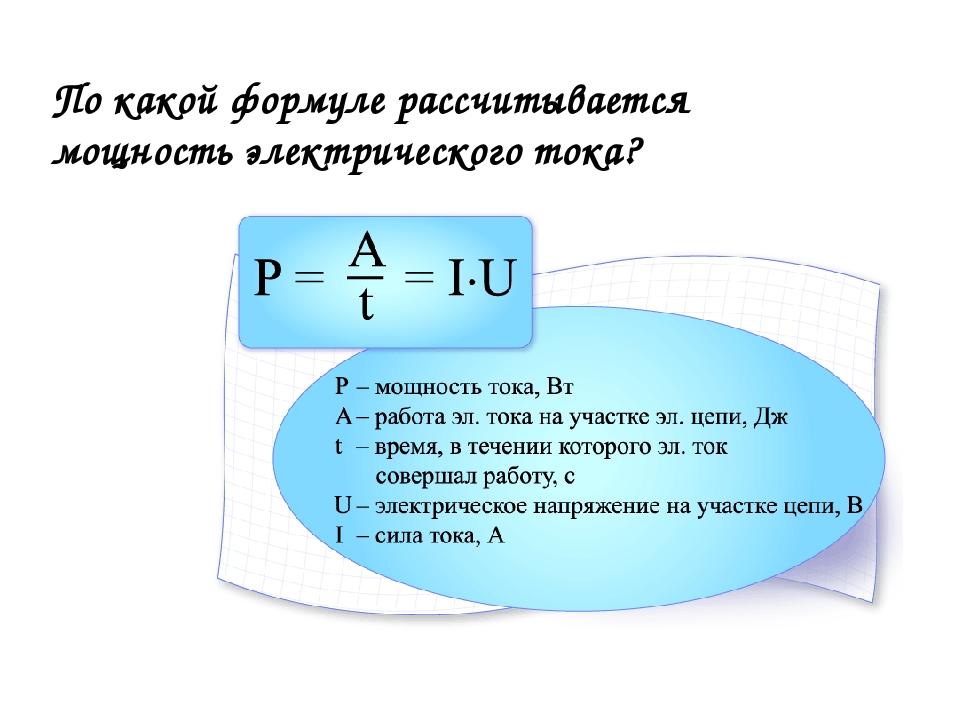
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.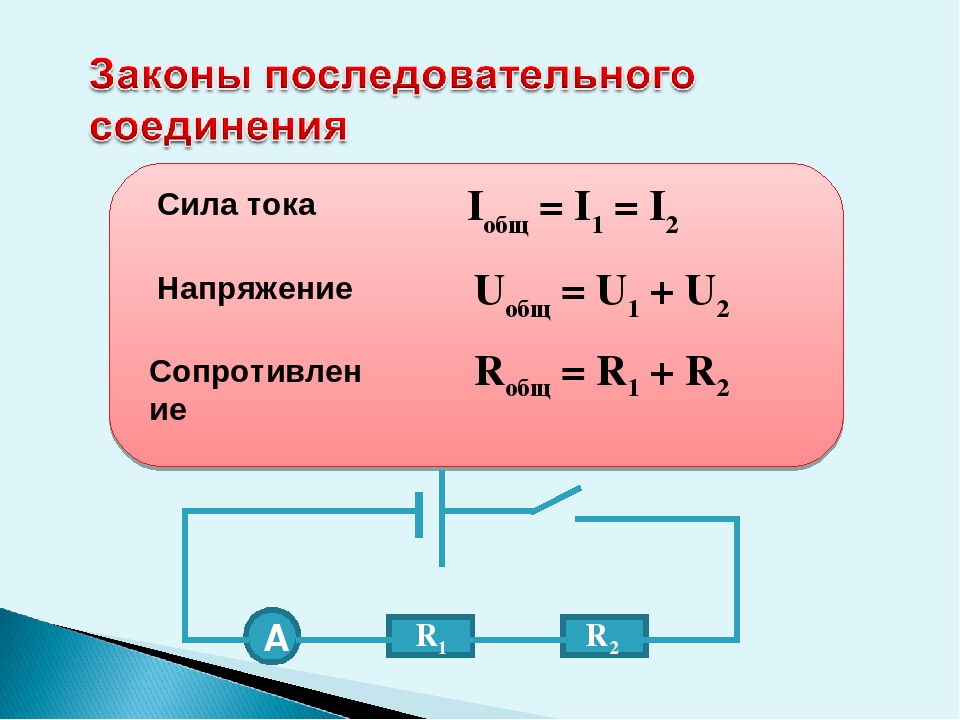
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.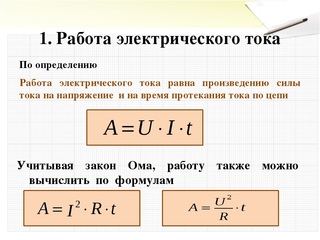
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.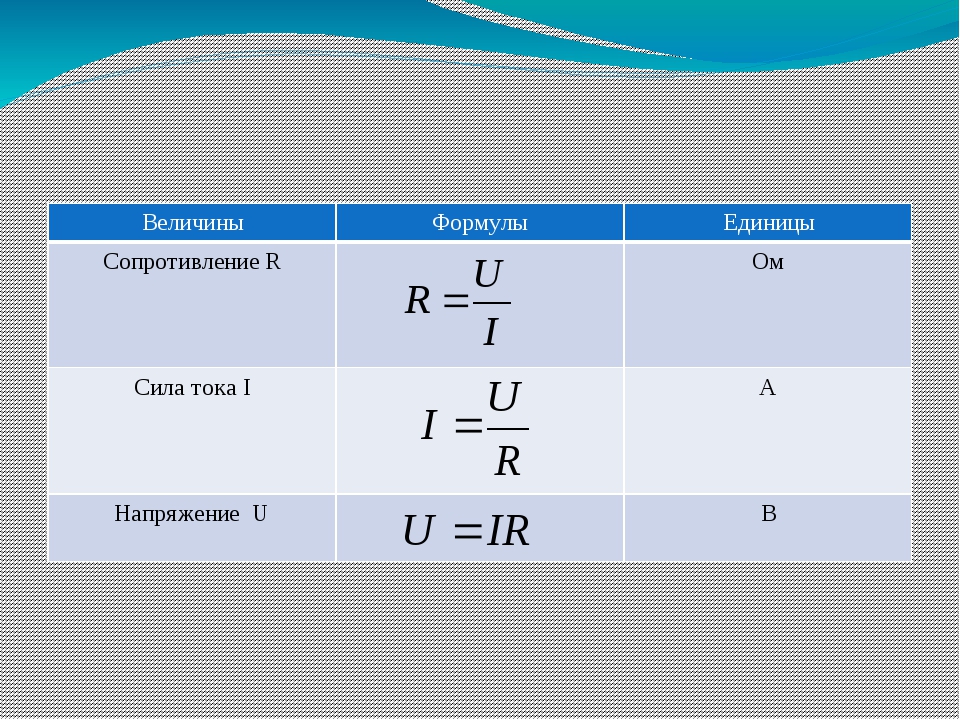
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность.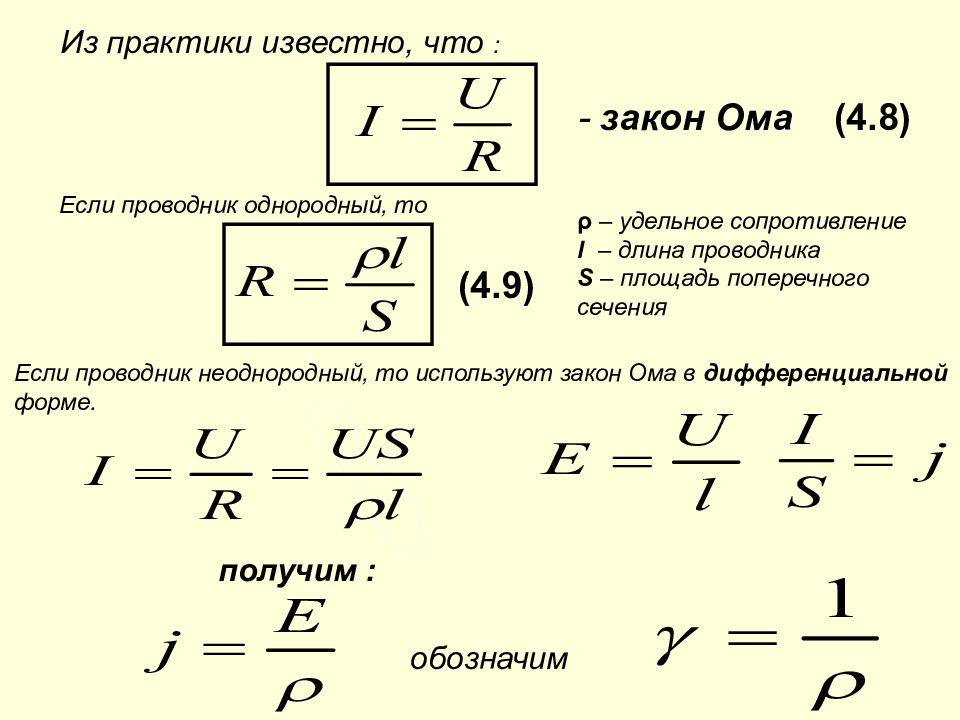 Для этого мы преобразуем выражение (5), используя формулу:
Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели.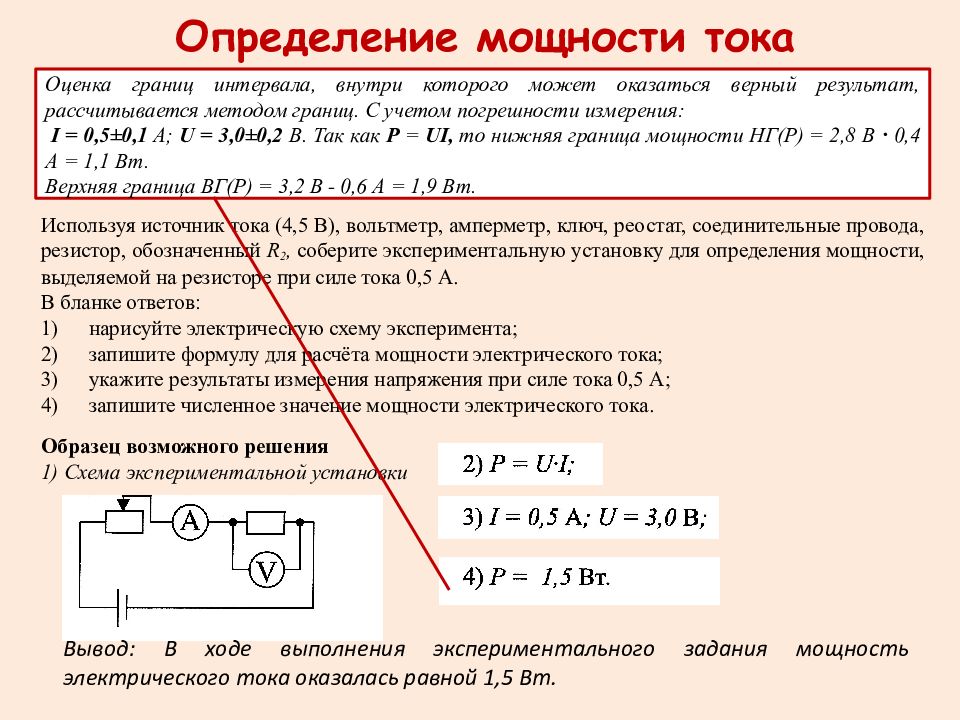 Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Расчет коэффициента полезного действия: формулы для электрической цепи
Для оценки эффективности расхода энергии на выполнение работы необходимо выяснить, как найти КПД. Полученные сведения пригодятся для оптимизации параметров электрических компонентов цепи, рычагов и других передаточных механизмов. С помощью предварительных вычислений можно увеличить длительность действия автономного источника питания, решить другие практические задачи.
Формула КПД поясняет основные определения
Что такое КПД источника тока
Неподвижный заряд не выполняет работу. Уменьшение энергетического запаса в аккумуляторе происходит за счет химических реакций.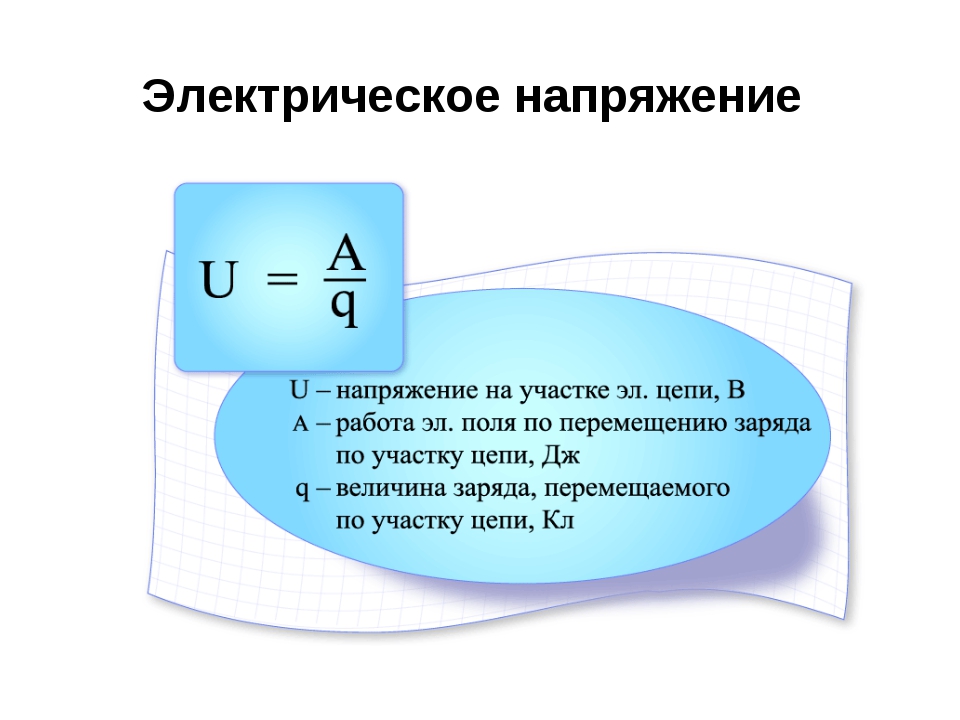 Фактически это свидетельство несовершенства конструкции.
Фактически это свидетельство несовершенства конструкции.
После подключения источника к проводникам с подключенной нагрузкой заряды перемещаются по цепи, выполняя определенную работу. Полезная составляющая мощности (Pпол) определяется параметрами внешнего контура. Полная (Pп) – содержит совокупные затраты. Если электротехник пользуется привычными терминами, он быстро установит для коэффициента полезного действия формулу:
КПД = Рпол/Рп = (U*I)/(Е*I) = U/E.
Для чего нужен расчет КПД
Наглядный пример недостаточно эффективного устройства – классическая лампа накаливания. Пропускание тока через вольфрамовую спираль повышает температуру проводника. В рабочем режиме значительное количество потребляемой мощности расходуется на генерацию излучения. Однако к видимой части диапазона относится только небольшая часть спектра. Так как вырабатываемая теплота не выполняет полезного действия, соответствующие энергетические затраты следует узнавать по излишним.
Если выразить КПД через мощность в этом случае, следует одновременно учесть долговечность. Эта методика повышает точность оценки, так как подразумевает необходимость периодической замены испорченного излучателя.
В типовом рабочем режиме лампа накаливания нагревает нить до 2600-2800К. При таком значении срок службы составляет 900-1200 часов, КПД – от 5 до 7%. Увеличить эффективность в 2-5 раз можно повышением температуры до 3400-3600К. Однако в этом варианте долговечность уменьшается до 5-6 часов. Подобные практические характеристики нельзя признать удовлетворительными.
Сравнение эффективности и других параметров разных типов ламп
Эта таблица демонстрирует превосходство экономичных источников света. Срок службы современных светодиодов измеряется десятками тысяч часов. Даже на завершающих этапах рабочих циклов обеспечиваются высокая яркость и качественное распределение спектральных составляющих.
Нахождение тока в полной цепи
Для изучения эффективности потребления энергии в электротехнике можно использовать базовые формулы. В полной цепи по базовому определению рассматривают источник тока (I) с внутренним сопротивлением (r). Подключенная нагрузка потребляет определенную мощность. Она характеризуется электрическим сопротивлением R.
В полной цепи по базовому определению рассматривают источник тока (I) с внутренним сопротивлением (r). Подключенная нагрузка потребляет определенную мощность. Она характеризуется электрическим сопротивлением R.
Прохождение тока по такой цепи обеспечивает энергия источника, которая определена значением электродвижущей силы (ЭДС – E). Ее можно выразить как отношение выполненной сторонними силами работы (A) по передвижению заряда (q) с положительным знаком по соответствующему контуру. С учетом известной формулы I= q/t несложно определить зависимость между рассматриваемыми величинами:
А = E * I * t,
где t – контрольный временной интервал.
Отдельно можно рассмотреть участки с внутренним и внешним сопротивлением. Каждый из них выделяет определенное законом Джоуля-Ленца количество теплоты Q = I2 * R * t. Так как энергия не пропадает бесследно, можно сделать правильный вывод о равенстве Q = A. Подставив значения в исходное выражение, получают:
Подставив значения в исходное выражение, получают:
E = I*R + I*r.
ЭДС полной цепи вычисляется сложением двух падений напряжений на внутреннем и внешнем участке. Элементарное преобразование позволяет узнать силу тока в соответствующем проводнике:
I = E/ (R+r).
Расчет КПД электрической цепи
После определения основных параметров можно перейти к изучению эффективности системы. Для вычисления КПД обозначение потребления электроэнергии удобно сделать по стандартным формулам.
Определить мощность можно по следующим соотношениям силы тока, напряжения, электрического сопротивления
Выполняемая работа в цепи определяется количеством перемещенных зарядов, а также скоростью данного процесса. Для объективной оценки последнего параметра измерения выполняют с учетом определенных временных интервалов (Δt). Работу и мощность можно определить следующими формулами:
- A = P * Δt;
- P = A / Δt.

Как и в классической механике, работу можно измерить в джоулях (Дж). Мощность, по стандартам СИ, указывают в ваттах (Вт). Зависимость между отмеченными единицами:
Вт = Дж/ с (для электрических цепей вольт * ампер).
Для обозначения КПД символ «η» применяют в типовых формулах. Базовое определение с учетом приведенных замечаний можно преобразовать следующим образом:
η = A / Q * 100%,
где:
- A – выполненная работа;
- Q – энергия, полученная из источника.
Как найти КПД, формула для полной цепи
Любое подключенное устройство характеризуется определенными потерями. Резистор выделяет тепло. Трансформатор тратит часть энергии на преобразование электромагнитных волн. На примере лампы накаливания показана низкая эффективность изделия. С применением КПД увеличивают объективность оценки разных систем, подключаемых потребителей, генераторов. В следующем пункте представлена технология проверки силовых агрегатов.
Методика и порядок измерений
Идеальные условия можно рассматривать только в теории. Для корректной оценки замкнутой системы необходимо учитывать энергетические потери на выполнение необходимой работы. Ниже показано, как определить КПД механических силовых агрегатов с применением разных исходных данных.
Движению поршня в блоке цилиндров двигателя внутреннего сгорания препятствует сила трения. Поступательно-возвратные движения в ходе стандартного цикла преобразуются во вращение вала с дополнительными потерями. Высокая температура не выполняет в данном случае полезные функции. Чтобы не допустить разрушения агрегата, необходимо поддерживать определенный тепловой режим. Приходится обеспечить циркуляцию охлаждающей жидкости с помощью помпы.
Понятно, что в подобном случае сделать общий КПД расчет с учетом каждого компонента конструкции непросто. Однако можно узнать в ходе эксперимента с высокой точностью, какое количество топлива (масса – m) придется затратить на 100 км пробега машины за соответствующее время (t). Далее нужно взять из сопроводительной документации (справочников) следующие данные:
Далее нужно взять из сопроводительной документации (справочников) следующие данные:
- мощность мотора – Рм;
- удельную теплоту бензина – У.
В этом варианте для расчета КПД двигателя формула преобразуется следующим образом:
η = (Pм * t) / (У * m).
Для отображения результата в % итоговое значение умножают на 100.
Если мощность силового агрегата не известна, определять эффективность можно по массе авто (Mа). Измерять ее несложно с помощью промышленных весов (на станции техосмотра, элеваторе). В ходе эксперимента разгоняются с места до контрольной скорости (v). Массу топлива вычисляют по объему (переведенному из литров в м кв.), который умножают на плотность (справочная величина в кг на куб. м).
В этом случае КПД расчет находят по формуле:
η = (Mа * v2)/(2 * У * m).
Следует перевести предварительно скорость из км/час в м/с.
Проще измеряется эффективность электродвигателя с паспортной мощностью (P). Его подключают к источнику питания с известным напряжением (U). После выхода на стабильную частоту вращения фиксируют значение тока (I) в цепи. Далее применяют классическую формулу:
Его подключают к источнику питания с известным напряжением (U). После выхода на стабильную частоту вращения фиксируют значение тока (I) в цепи. Далее применяют классическую формулу:
η = P/ (U * I).
Если сопроводительная документация отсутствует, технические параметры берут с официального сайта производителя. Однако и в этом случае следует понимать ограниченную точность подобных данных. В процессе эксплуатации характеристики могут ухудшиться за счет естественного износа. Погрешность увеличивается после длительной интенсивной эксплуатации, при подключении редуктора или другого переходного устройства.
Значительно улучшить точность можно с применением простой методики:
- устанавливают на вал шкив с закрепленным тросом;
- поднимают на контрольную высоту (h) груз c массой m;
- секундомером фиксируют время (t) на выполнение этой работы;
- мультиметром измеряют напряжение (U) и силу тока (I) на клеммах источника питания и в разрыве цепи, соответственно.

Для нахождения КПД в физике формула выглядит следующим образом:
η = (m * h * g)/(I * U * t),
где g – это гравитационная постоянная (9,80665).
Эффективность любого силового агрегата определяют по соотношению полезной работы к расходованной энергии. Чтобы корректно определять класс техники, пользуются переводом в проценты. Следует подчеркнуть, что значение больше 100% обозначает ошибку в расчетах. Создатель подобного агрегата станет «властелином мира», так как изобретет вечный двигатель.
Видео
Работа и мощность электрического тока. Единицы работы электрического тока
1139. Через электрическую цепь с напряжением 220 В прошел заряд 2500 Кл. Найдите работу электрического тока в цепи.
Через электрическую цепь с напряжением 220 В прошел заряд 2500 Кл. Найдите работу электрического тока в цепи.
1140. Сила тока в электрической цепи тостера равна 6 А. Напряжение в цепи 220 В. Чему равна работа электрического тока в цепи за 5 минут?
1141. Никелиновый и медный провода одинакового сечения и длины включены в цепь последовательно. Какой из проводов сильнее нагреется? Почему?
Никелиновый нагревается сильнее т.к его сопротивление больше.
1142. При включенном освещении через провода и нить электролампы проходит ток одинаковой силы. При этом провода почти не нагреваются, а нить лампы накаляется добела. Почему?
Сопротивление в нити лампочки больше сопротивления проводов.
1143. Включенный в сеть утюг непрерывно выделяет теплоту. Почему его обмотка не перегорает?
Потому что в процессе работы не достигается температуры плавления.
1144. Кипятильник, состоящий из помещенной в кожух никелиновой спирали, опущен в сосуд с водой. Какой максимальной температуры может достигнуть кипятильник, когда он в воде? Почему?
Кипятильник, состоящий из помещенной в кожух никелиновой спирали, опущен в сосуд с водой. Какой максимальной температуры может достигнуть кипятильник, когда он в воде? Почему?
Температуры кипения воды 100 градусов. Температура не поднимается выше, пока вся вода не перейдет в пар.
1145. Если включенный в сеть кипятильник остается без воды, он раскаляется и перегорает. Почему?
Тепло не будет отводиться, спираль нагреется и разрушится.
1146. При изменении напряжения меняется ли мощность, потребляемая прибором? Почему?
1147. Электрическая лампа соединена параллельно с реостатом (рис. 132). Напряжение на данном участке цепи постоянно….
Нет, т.к. лампочка включена в цепь параллельно реостату.
1148. Реостат и электролампа соединены последовательно (рис. 133). Напряжение на клеммах поддерживается постоянным…
Да. Т.к. лампочка включена в цепь последовательно и с изменением сопротивления на реостате, будет меняться ток во всей цепи.
1149. Если укоротить спираль электроплитки, изменится ли ее накал во включенном состоянии? Если изменится, то как?
1150. В квартире не горит свет и не включены в розетки никакие приборы, а вполне исправный счетчик вращается. На что это указывает? Что надо предпринять в данном случае?
Неисправна проводка. Проверить проводку
1151. Почему проволочки из легкоплавких металлов применяют в качестве предохранителей для электрической цепи?
При прохождении тока выше нормы они расплавятся, разомкнув цепь.
1152. Можно ли вместо перегоревшего предохранителя вставить толстую проволоку?
Это чревато выходом из строя других элементов цепи.
1153. Можно ли в электрическом предохранителе заменить перегоревшую свинцовую проволочку медной проволочкой такой же длины и сечения?
1154. Проводка цепи осветительной сети рассчитана на максимальную силу тока 7 А. Можно ли в такой сети поставить предохранитель на 6 А? Можно ли его заменить предохранителем на 20 А?
Нет. Предохранитель не выдержит максимально допустимый ток 7 А, а предохранитель на 20 А не сработает при превышении тока от 7 до 20 А.
Предохранитель не выдержит максимально допустимый ток 7 А, а предохранитель на 20 А не сработает при превышении тока от 7 до 20 А.
1155. В работающей электрической сети стоит предохранитель на 20 А. Что произойдет, если его заменить предохранителем на 6 А?
Он перегорит при токе свыше 6А.
1156. При включении магнитофона в сеть с напряжением 220 В через его электрическую цепь прошел заряд 2500 Кл. Чему равна работа электрического тока в цепи?
1157. Сила тока в электрической цепи ростера равна 6 А. Напряжение в сети 220 В. Чему равна работа электрического тока за пять минут?
1158. При напряжении 220 В сила тока в двигателе тепловентилятора равна 0,1 А. Какую работу совершает электрический ток в электродвигателе в течение 30 с?
1159. Напряжение на клеммах электродвигателя равно 12 В, сила тока в цепи электродвигателя 0,5 А. Определите работу электродвигателя за 20 минут.
1160. На спирали лампочки холодильника напряжение равно 3,5 В, сопротивление спирали 14 Ом. Какую работу совершает ток в лампочке за 2 минуты?
1161. Электрическая духовка подключена к цепи с напряжением 220 В, сила тока равна 10 А. Сколько энергии расходует электродуховка за 5 ч?
1162. Работа тока в приборе за 15 минут равна 40 500 Дж, напряжение на его концах 15 В. Какой силы ток был пропущен через прибор?
1163. При включении настольной лампы в сеть с напряжением 220 В через нее пошел ток силой 0,5 А. При этом была израсходована энергия 330 Дж. Какое время работала лампа?
1164. Коридорная лампочка мощностью 50 Вт ежедневно горит в среднем 5 часов. Сколько нужно заплатить за месяц (30 дней) горения лампы? Стоимость энергии взять по существующим тарифам.
1165. Сколько энергии потребляет за 60 минут лампа мощностью 60 Вт?
1166. Рассчитайте работу тока в воздухоочистителе за 2 ч, если мощность воздухоочистителя равна 0,4 кВт. Сколько при этом расходуется энергии?
Сколько при этом расходуется энергии?
1167. Какова мощность тока в телевизоре, включенном в цепь с напряжением 220 В, при силе тока 0,4 А?
1168. Через электрическую лампочку, включенную в осветительную сеть, протекло 5 Кл электричества, причем было израсходовано 600 Дж электрической энергии. Определите напряжение в сети.
1169. Через лампочку карманного фонаря протекло 5 Кл электричества, причем батарея израсходовала 20 Дж электрической энергии. Определите, какое напряжение дает батарея карманного фонаря.
1170. При напряжении 120 В в электрической лампочке в течение 30 с израсходовано 1800 Дж энергии. Определите, какое количество электричества протекло по нити лампочки и чему была равна сила тока.
1171. Пользуясь понятиями напряжение и сила тока, поясните, почему мощность тока выражается произведением IU.
Электрический ток, протекая от высшего потенциала к низшему, совершает работу. Количество электричества, проходящего через поперечное сечение проводника — сила тока, следовательно мощность будет прямопропорциональна силе тока.
1172. Какая мощность расходуется лампочкой, потребляющей 0,5 А, если напряжение на клеммах лампочки 110 В?
1173. Мотор, включенный в сеть тока с напряжением 110 В берет ток в 7,35 А. Определите мощность мотора.
1174. Лампочка требует мощность 100 Вт. Какой ток будет идти по лампочке, если ее включить в сеть с напряжением 110 В?
1175. Какова мощность тока в электрочайнике, рассчитанном на напряжение 127 В и силу тока 1,0 А?
1176. В трамвайном двигателе сила тока через обмотки равна 80 А при напряжении 500 В. Какова мощность тока?
1177. Сила тока в электроприборе равна 8 А. Напряжение в сети 110 В. Определите мощность тока.
1178. Стоваттная лампочка включена в сеть с напряжением 120 В. Какой ток течет через лампочку?
1179. Первая лампочка рассчитана на напряжение 24 В и силу тока 800 мА, вторая рассчитана на напряжение 60 В и силу тока 0,2 А. Какая из лампочек потребляет большую мощность и во сколько раз?
Какая из лампочек потребляет большую мощность и во сколько раз?
1180. Какова мощность тока, питающего электрочайник с сопротивлением нагревательного элемента 44 Ом при напряжении 220 В?
1181. На этикетке СВЧ-печки написано: 220 В, 1000 Вт. Найдите сопротивление СВЧ-печки и силу тока в ее электрической цепи.
1182. Мощность настольной лампы 60 Вт. Каково ее сопротивление, если напряжение в сети 120 В?
1183. По какой формуле можно вычислить мощность тока на участке проводника, если известна сила тока и сопротивление данного участка проводника?
1184. По обмотке электрической печи сопротивлением 300 Ом идет ток 5 А. Вычислите, какую мощность потребляет печь.
1185. По какой формуле можно вычислить мощность тока на участке проводника, если известно напряжение на концах участка цепи и сопротивление данного участка проводника?
1186. Какую мощность потребляет электролобзик сопротивлением 240 Ом при напряжении 120 В?
1187. Реостат потребляет мощность 60 Вт при напряжении на зажимах 90 В. Каково сопротивление реостата?
Реостат потребляет мощность 60 Вт при напряжении на зажимах 90 В. Каково сопротивление реостата?
1188. Пять нагревателей по 100 Вт каждый включены параллельно. Напряжение в сети 220 В. Найдите силу тока в цепи.
1189. На рисунке 134 изображены две схемы включения в цепь трех одинаковых лампочек. В какой лампе больше мощность тока и во сколько раз? Рассмотреть случай (а) и случай (б).
1190. Сила тока в обмотке электромотора равна 12,5 А при напряжении на полюсах 110 В. Какую работу совершит ток в течение 1 ч 30 мин и какова его мощность?
1191. Лампочка мощностью 60 Вт горит 4 ч в сутки; вторая лампочка мощностью 40 Вт горит в среднем 6 ч в сутки. Сколько энергии потребляют обе лампочки за 30 дней? Сколько надо заплатить за горение лампочек в месяц при современном тарифе?
1192. При расходе энергии в 100 Вт в час счетчик делает 480 оборотов. Сколько оборотов сделает счетчик, если в течение 8 ч будут непрерывно гореть две 60-ваттные лампочки?
1193. При напряжении 500 В средняя сила тока в обмотке электродвигателя троллейбуса равна 150 А. Рассчитайте по современным тарифам стоимость работы двигателя в течение 8 ч.
При напряжении 500 В средняя сила тока в обмотке электродвигателя троллейбуса равна 150 А. Рассчитайте по современным тарифам стоимость работы двигателя в течение 8 ч.
1194. Электрический нагреватель сопротивлением 20 Ом питается током в 6 А. Какое количество теплоты выделится в нагревателе в течение 2 мин?
1195. Через электрический утюг сопротивлением 24 Ом проходит ток силой 5 А. Какое количество теплоты в течение часа выделит утюг?
1196. В проволоке сопротивлением 1 Ом за 1 с выделяется количество теплоты, равное 4 Дж. Какова сила тока, проходящего через проволоку?
1197. Сколько тепла выделит электропечь за 1 мин, если ее сопротивление 20 Ом, а сила тока 6 А?
1198. Ток силой 5 А проходит через проволочную спираль сопротивлением 20 Ом. Какое количество теплоты выделит спираль за 20 мин?
1199. Сила тока в электролампе равна 1 А при напряжении 110 В. Какое количество теплоты выделяется в ее нити в течение часа?
1200. Напряжение в сети электрички 200 В. Для отопления вагона необходимо в час количество теплоты, равное 8,38 МДж. Какая сила тока необходима для отопления? Каково должно быть сопротивление нагревательного прибора?
Напряжение в сети электрички 200 В. Для отопления вагона необходимо в час количество теплоты, равное 8,38 МДж. Какая сила тока необходима для отопления? Каково должно быть сопротивление нагревательного прибора?
1201. Электрическая печь сопротивлением 30 Ом включена в есть напряжением 110 В. Какое количество теплоты выделяет печь в одну минуту?
1202. Через никелиновую проволоку длиной 1 м и площадью поперечного сечения 0,45 мм2 проходит ток силой 4 А. Какое количество теплоты при этом выделяется за 1 мин?
1203. Два одинаковых электронагревателя с сопротивлением 40 Ом включены: первый — в сеть с напряжением 120 В, второй – в сеть с напряжением 240 В. В каком нагревателе будет выделяться большее количество теплоты за одинаковое время? Во сколько раз?
1204. В сеть с напряжением 120 В последовательно включены две лампы, первая с сопротивлением 400 Ом, вторая с сопротивлением 100 Ом. В какой лампе за одно и то же время будет выделяться большее количество теплоты?
1205.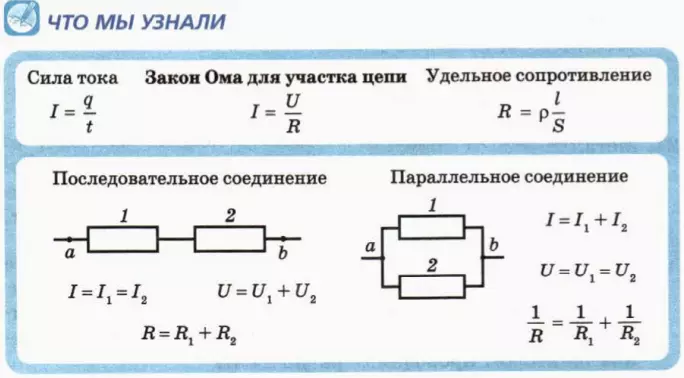 В одну цепь последовательно включены никелиновая проволока (длина 1 м, сечение 1 мм2 ). В какой из проволок выделится больше теплоты за одинаковое время?
В одну цепь последовательно включены никелиновая проволока (длина 1 м, сечение 1 мм2 ). В какой из проволок выделится больше теплоты за одинаковое время?
1206. Спиральная никелиновая проволока, через которую пропускается ток силой 2 А при напряжении 2 В, опущена в 1 л керосина. На сколько градусов нагреется керосин за 10 мин?
1207. В электрическом чайнике объемом 2 л воды нагревается с 20°С до кипения за 10 мин. какой силы ток в электрочайнике при напряжении сети 120 В?
1208. Кипятильник с сопротивлением 10 Ом, опущенный в 1 л воды, нагревает ее от 20°С до кипения при напряжении 110В. Сколько времени займет этот процесс?
1209. Кипятильник, включенный в сеть с напряжением 110 В, нагревает 200 г воды с начальной температурой 20 °С до кипения за 1 мин. каково сопротивление проволоки кипятильника?
1210. Для изготовления нагревательного прибора, который при напряжении 120 В мог бы нагреть 1 л воды от 20°С до кипения за 5 мин, используют никелиновую проволоку сечением 0,2 мм² . Какова длина проволоки?
Какова длина проволоки?
1211. При напряжении 220 В и силе тока 5 А полезная мощность электродвигателя равна 0,46 кВт. Какова КПД электродвигателя?
1212. При напряжении 220 В сила тока в электродвигателе 1,25 А, КПД равен 40%. Какую полезную работу совершает электродвигатель за 25 мин?
1213. При напряжении 110 В через двигатель идет тока в 12,5 А. Какова полезная мощность двигателя, если его КПД 58%?
1214. Водонагреватель при силе тока 5 А и напряжении 220 В может нагреть 600 г воды от 12°С до кипения за 8 мин. Каков КПД водонагревателя?
1215. Определите КПД электрочайника, в котором при силе тока 4 А и напряжении 120 В нагрелось 720 г воды от 20°С до 100°С за 15 мин.
1216. Плоский конденсатор состоит из двух параллельно расположенных в воздухе пластинок, каждая площадью 100 см2 , расстояние между ними 0,2 см. определите емкость конденсатора.
1217. Определите, какой из двух конденсаторов обладает большей емкостью. Первый представляет собой стеклянную пластинку, покрытую с обеих сторон металлическими листами, каждый площадью S = 500 см2. Толщина стекла d = 4 мм, диэлектрическая постоянная 8 = 7. Второй конденсатор представляет собой лист парафинированной бумаги, на которую с обеих сторон положено по металлическому листу площадью S = 250 см2. Толщина листа бумаги d = 0,2 мм, диэлектрическая постоянная парафина е = 2.
Первый представляет собой стеклянную пластинку, покрытую с обеих сторон металлическими листами, каждый площадью S = 500 см2. Толщина стекла d = 4 мм, диэлектрическая постоянная 8 = 7. Второй конденсатор представляет собой лист парафинированной бумаги, на которую с обеих сторон положено по металлическому листу площадью S = 250 см2. Толщина листа бумаги d = 0,2 мм, диэлектрическая постоянная парафина е = 2.
1218. Определите емкость конденсатора, состоящего из п параллельных пластин, по следующим данным:
1) S = 50 см2, е = 5, d = 0,002 см, п = 20;
2) S = 0,2 м2, в = 7, d = 0,1 мм и п = 100.
1219. Определить емкость конденсаторов по следующим данным:
1) S=5 см2, n=33, d=0.03 мм, e=1;
2) S=10 cм2 , n=15, d=0.004 мм, e=6.
1220. Для радиоприемника требуется изготовить постоянный конденсатор с парафинированной бумагой емкостью С, равно 2200 пФ, если S=4 см² и d=0,05 мм. Сколько нужно сделать для этого пластин?
1221. Определить число пластин так называемого блокировочного конденсатора, рассчитанного на емкость 440 пФ, если площадь пластины S=4 см² , d=0,02 см и e=4.
1222. Емкость конденсатора 10 мкФ. Как изменится его емкость, если парафинированную бумагу заменить пластинками слюды, имеющими ту же толщину, что и парафинированная бумага? (Диэлектрическая проницательность слюды e=6)
1223*. Определить емкость лейденской банки по следующим данным: высота 40 см, диаметр наружной цилиндрической поверхности 20 см, толщина стенок стекла 3 мм, диэлектрическая постоянная стекла 5.
1224. Конденсатор емкостью С=100 мкФ заряжен до потенциала U=90 кВ. Определите его заряд в кулонах.
1225. Конденсатор емкостью С=2640 пФ подключен к сети городского тока, напряжение в которой U=120 В. Определите заряд конденсатора в кулонах.
Как узнать мощность и ток трансформатора по его внешнему виду
Слово “трансформатор” образуется от английского слова “transform” – преобразовывать, изменяться. Но дело в том, что сам трансформатор не может как-либо измениться либо поменять форму и так далее.
Он обладает еще более удивительный свойством – преобразует переменное напряжение одного значения в переменное напряжение другого значения.
Ну разве это не чудо? В этой статье мы будем рассматривать именно трансформаторы напряжения.
Трансформатор напряжения
Трансформатор напряжения можно отнести больше к электротехнике, чем к электронике. Самый обыкновенный однофазный трансформатор напряжения выглядит вот так.
- Если откинуть верхнюю защиту трансформатора, то мы можем четко увидеть, то он состоит из какого-то железного каркаса, который собран из металлических пластин, а также из двух катушек, которые намотаны на этот железный каркас. Здесь мы видим, что из одной катушки выходит два черных провода
- а с другой катушки два красных провода
- Эти обе катушки одеваются на сердечник трансформатора. То есть в результате мы получаем что-то типа этого
- Ничего сложного, правда ведь?
Но дальше самое интересное. Если подать на одну из этих катушек переменное напряжение, то в другой катушке тоже появляется переменное напряжение. Но как же так возможно? Ведь эти обмотки абсолютно не касаются друг друга и они изолированы друг от друга. Во чудеса! Все дело, в так называемой электромагнитной индукции.
Если подать на одну из этих катушек переменное напряжение, то в другой катушке тоже появляется переменное напряжение. Но как же так возможно? Ведь эти обмотки абсолютно не касаются друг друга и они изолированы друг от друга. Во чудеса! Все дело, в так называемой электромагнитной индукции.
Если объяснить простым языком, то когда на первичную обмотку подают переменное напряжение, то в сердечнике возникнет переменное магнитное поле с такой же частой. Вторая катушка улавливает это переменное магнитное поле и уже выдает переменное напряжение на своих концах.
Обмотки трансформатора
Эти самые катушки с проводом в трансформаторе называются обмотками. В основном обмотки состоят из медного лакированного провода. Такой провод находится в лаковой изоляции, поэтому, провод в обмотке не коротит друг с другом. Выглядит такой обмоточный трансформаторный провод примерно вот так.
Он может быть разного диаметра. Все зависит от того, на какую нагрузку рассчитан тот или иной трансформатор.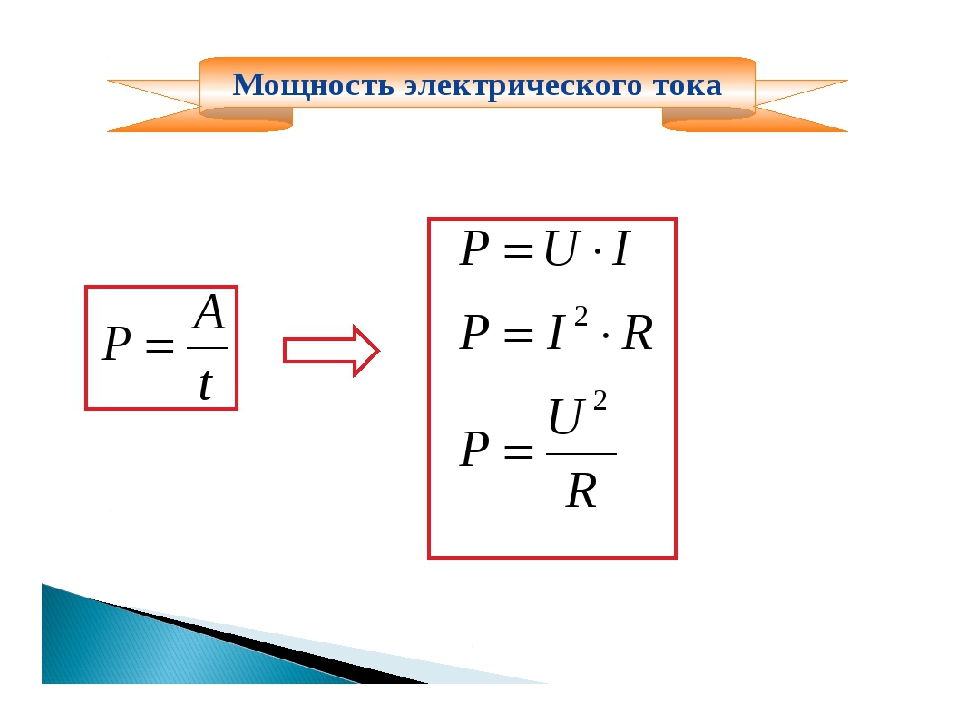
У самого простого однофазного трансформатора можно увидеть две такие обмотки.
Обмотка, на которую подают напряжение называется первичной. В народе ее еще называют “первичка”. Обмотка, с которой уже снимают напряжение называется вторичной или “вторичка”.
Для того, чтобы узнать, где первичная обмотка, а где вторичная, достаточно посмотреть на шильдик трансформатора.
I/P: 220М50Hz (RED-RED) – это говорит нам о том, что два красных провода – это первичная обмотка трансформатора, на которую мы подаем сетевое напряжение 220 Вольт. Почему я думаю, что это первичка? I/P – значит InPut, что в переводе “входной”.
O/P: 12V 0,4A (BLACK, BLACK) – вторичная обмотка трансформатора с выходным напряжением в 12 Вольт (OutPut). Максимальная сила тока, которую может выдать в нагрузку этот трансформатор – это 0,4 Ампера или 400 мА.
Как работает трансформатор
Чтобы разобраться с принципом работы, давайте рассмотрим рисунок.
Здесь мы видим простую модель трансформатора. Подавая на вход переменное напряжение U1 в первичной обмотке возникает ток I1 .
Так как первичная обмотка намотана на замкнутый магнитопровод, то в нем начинает возникать магнитный поток, который возбуждает во вторичной обмотке напряжение U2 и ток I2 .
Как вы можете заметить, между первичной и вторичной обмотками трансформатора нет электрического контакта. В электронике это называется гальванически развязаны.
Формула трансформатора
- Главная формула трансформатора выглядит так.
- где
- U2 – напряжение на вторичной обмотке
- U1 – напряжение на первичной обмотке
- N1 – количество витков первичной обмотки
- N2 – количество витков вторичной обмотки
- k – коэффициент трансформации
- В трансформаторе соблюдается также закон сохранения энергии, то есть какая мощность заходит в трансформатор, такая мощность выходит из трансформатора:
Эта формула справедлива для идеального трансформатора.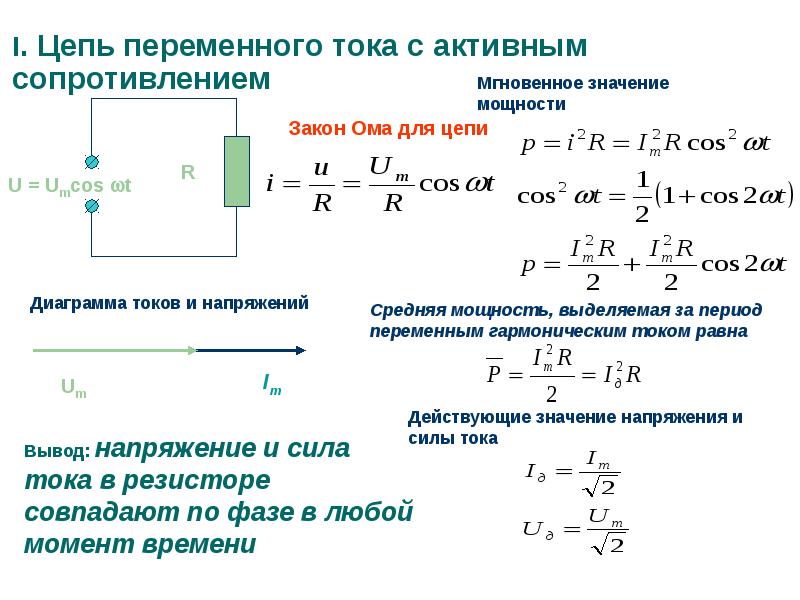 Реальный же трансформатор будет выдавать на выходе чуть меньше мощности, чем на его входе. КПД трансформаторов очень высок и порой составляет даже 98%.
Реальный же трансформатор будет выдавать на выходе чуть меньше мощности, чем на его входе. КПД трансформаторов очень высок и порой составляет даже 98%.
Типы трансформаторов по конструкции
Однофазные трансформаторы
Это трансформаторы, которые преобразуют однофазное переменное напряжение одного значения в однофазное переменное напряжение другого значения.
В основном однофазные трансформаторы имеют две обмотки, первичную и вторичную. На первичную обмотку подают одно значение напряжения, а со вторичной снимают нужное нам напряжение. Чаще всего в повседневной жизни можно увидеть так называемые сетевые трансформаторы, у которых первичная обмотка рассчитана на сетевое напряжение, то есть 220 В.
- На схемах однофазный трансформатор обозначается так:
- Первичная обмотка слева, а вторичная – справа.
Иногда требуется множество различных напряжений для питания различных приборов.
Зачем ставить на каждый прибор свой трансформатор, если можно с одного трансформатора получить сразу несколько напряжений? Поэтому, иногда вторичных обмоток бывает несколько пар, а иногда даже некоторые обмотки выводят прямо из имеющихся вторичных обмоток.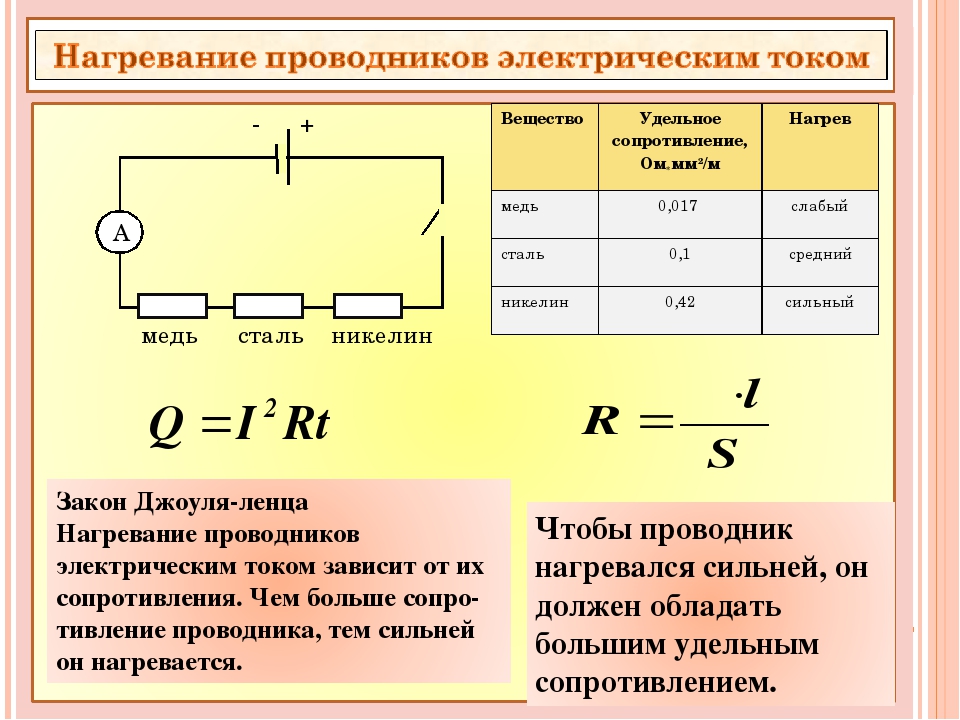 Такой трансформатор называется трансформатором со множеством вторичных обмоток. На схемах можно увидеть что-то подобное:
Такой трансформатор называется трансформатором со множеством вторичных обмоток. На схемах можно увидеть что-то подобное:
Трехфазные трансформаторы
Эти трансформаторы в основном используются в промышленности и чаще всего превосходят по габаритам простые однофазные трансформаторы. Почти все трехфазные трансформаторы считаются силовыми. То есть они используются в цепях, где нужно питать мощные нагрузки. Это могут быть станки ЧПУ и другое промышленное оборудование.
- На схемах трехфазные трансформаторы обозначаются вот так:
- Первичные обмотки обозначаются заглавными буквами, а вторичные обмотки – маленькими буквами.
- Здесь мы видим три типа соединения обмоток (слева-направо)
- звезда-звезда
- звезда-треугольник
- треугольник-звезда
В 90% случаев используется именно звезда-звезда.
Типы трансформаторов по напряжению
Понижающий трансформатор
Это трансформатор, которые понижает напряжение.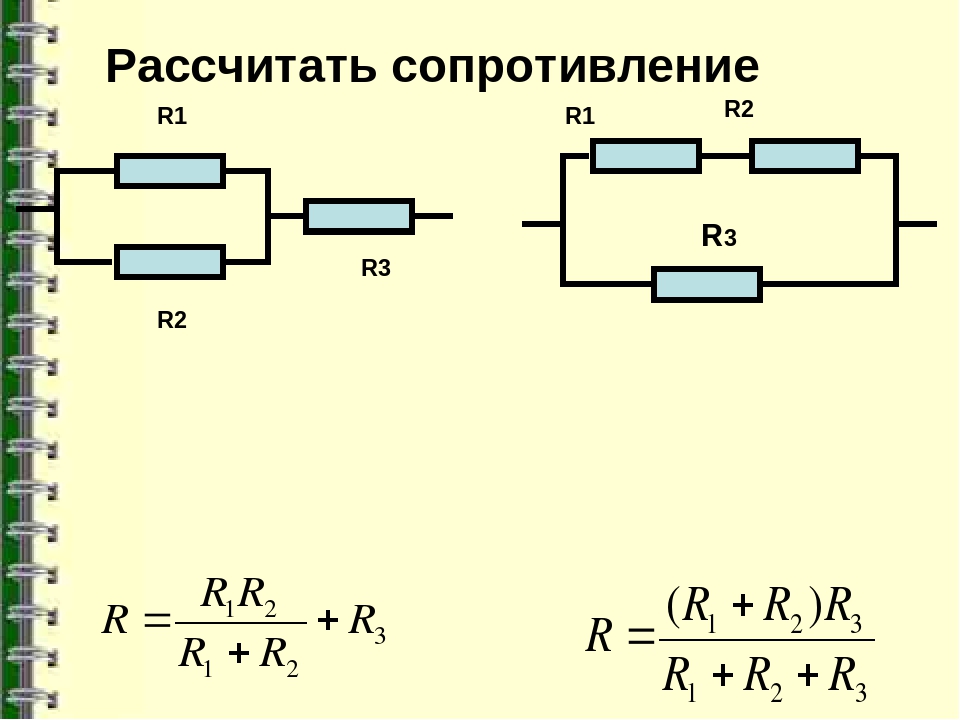 Допустим, на первичную обмотку мы подаем 220 Вольт, а снимаем 12 Вольт. В этом случае коэффициент трансформации (k) будет больше 1.
Допустим, на первичную обмотку мы подаем 220 Вольт, а снимаем 12 Вольт. В этом случае коэффициент трансформации (k) будет больше 1.
Повышающий трансформатор
Это трансформатор, который повышает напряжение. Допустим, на первичную обмотку мы подаем 10 Вольт, а со вторичной снимаем уже 110 В. То есть мы повысили наше напряжение 11 раз. У повышающих трансформаторов коэффициент трансформации меньше 1.
Разделительный или развязывающий трансформатор
Такой трансформатор используется в целях электробезопасности. В основном это трансформатор с одинаковым числом обмоток на входе и выходе, то есть его напряжение на первичной обмотке будет равняться напряжению на вторичной обмотке.
Нулевой вывод вторичной обмотки такого трансформатора не заземлен. Поэтому, при касании фазы на таком трансформаторе вас не ударит электрическим током. Про его использование можете прочесть в статье про ЛАТР.
У развязывающих трансформаторов коэффициент трансформации равен 1.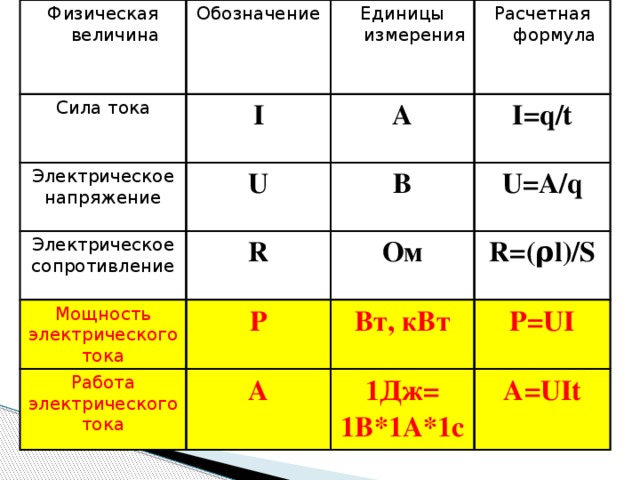
Согласующий трансформатор
Такой трансформатор используется для согласования входного и выходного сопротивления между каскадами схем.
Работа понижающего трансформатора на практике
Понижающий трансформатор – это такой трансформатор, который выдает на выходе напряжение меньше, чем на входе. Коэффициент трансформации (k) у таких трансформаторов больше 1 . Понижающие трансформаторы – это самый распространенный класс трансформаторов в электротехнике и электронике. Давайте же рассмотрим, как он работает на примере трансформатора 220 В —> 12 В .
- Итак, имеем простой однофазный понижающий трансформатор.
- Именно на нем мы будем проводить различные опыты.
Подключаем красную первичную обмотку к сети 220 Вольт и замеряем напряжение на вторичной обмотке трансформатора без нагрузки. 13, 21 Вольт, хотя на трансформаторе написано, что он должен выдавать 12 Вольт.
- Теперь подключаем нагрузку на вторичную обмотку и видим, что напряжение просело.
Интересно, какую силу тока кушает наша лампа накаливания? Вставляем мультиметр в разрыв цепи и замеряем.
Если судить по шильдику, то на нем написано, что он может выдать в нагрузку 400 мА и напряжение будет 12 Вольт, но как вы видите, при нагрузку близкой к 400 мА у нас напряжение просело почти до 11 Вольт. Вот тебе и китайский трансформатор. Нагружать более, чем 400 мА его не следует. В этом случае напряжение просядет еще больше, и трансформатор будет греться, как утюг.
Как проверить трансформатор
Как проверить на короткое замыкание обмоток
Хотя обмотки прилегают очень плотно к друг другу, их разделяет лаковый диэлектрик, которым покрываются и первичная и вторичная обмотка.
Если где-то возникло короткое замыкание между проводами, то трансформатор будет сильно греться или издавать сильный гул при работе. Также он будет пахнуть горелым лаком.
В этом случае стоит замерить напряжение на вторичной обмотке и сравнить, чтобы оно совпадало с паспортным значением.
Проверка на обрыв обмоток
При обрыве все намного проще. Для этого с помощью мультиметра мы проверяем целостность первичной и вторичной обмотки. Итак, сопротивление первичной обмотки нашего трансформатора чуть более 1 КОм. Значит обмотка целая.
- Таким же образом проверяем и вторичную обмотку.
- Отсюда делаем вывод, что наш трансформатор жив и здоров.
Как прозвонить трансформатор или как определить обмотки трансформатора
Здравствуйте, уважаемые читатели сайта sesaga.ru.
На первых порах занятий радиоэлектроникой у начинающих радиолюбителей, да и не только у радиолюбителей, возникает очень много вопросов, связанных с прозвонкой или определением обмоток трансформатора. Это хорошо, если у трансформатора всего две обмотки.
А если их несколько, да и еще у каждой обмотки несколько выводов. Тут просто караул кричи. В этой статье я расскажу Вам, как можно определить обмотки трансформатора визуальным осмотром и с помощью мультиметра.
Как Вы знаете, трансформаторы предназначены для преобразования переменного напряжения одной величины в переменное напряжение другой величины.
Самый обычный трансформатор имеет одну первичную и одну вторичную обмотки. Питающее напряжение подается на первичную обмотку, а ко вторичной обмотке подключается нагрузка.
На практике же большинство трансформаторов может иметь несколько обмоток, что и вызывает затруднение в их определении.
1. Определение обмоток визуальным осмотром
При визуальном осмотре трансформатора обращают внимание на его внешний защитный слой изоляции, потому как у некоторых моделей на внешнем слое изображают электрическую схему с обозначением всех обмоток и выводов; у некоторых моделей выводы обмоток только маркируют цифрами. Также можно встретить старые отечественные трансформаторы, на внешнем слое которых указывают маркировку в виде цифрового кода, по которому в справочниках для радиолюбителей есть вся информация о конкретном трансформаторе.
Если трансформатор попался без опознавательных знаков, то обращают внимание на диаметр обмоточного провода, которым намотаны обмотки.
Диаметр провода можно определить по выступающим выводам концов обмоток, выпущенных для закрепления на контактных лепестках, расположенных на элементах каркаса трансформатора.
Как правило, первичную обмотку мотают проводом меньшего сечения, по отношению к вторичной. Диаметр провода вторичной обмотки всегда больше.
Исключением могут быть повышающие трансформаторы, работающие в схемах преобразователей напряжения и тока. Их первичная обмотка выполнена толстым проводом, так как генерирует высокое напряжение во вторичной обмотке. Но такие трансформаторы встречаются очень редко.
При изготовлении трансформаторов первичную обмотку, как правило, мотают первой. Ее легко определить по выступающим концам выводов обмотки, расположенных ближе к магнитопроводу. Вторичную обмотку наматывают поверх первичной, и поэтому концы ее выводов расположены ближе к внешнему слою изоляции.
В некоторых моделях сетевых трансформаторов, используемых в блоках питания бытовой радиоаппаратуры, обмотки располагают на пластмассовом каркасе, разделенном на две части: в одной части находится первичная обмотка, а в другой вторичная. К выводам первичной обмотки припаивают гибкий монтажный провод, а выводы вторичной обмотки оставляют в виде обмоточного провода.
2. Определение обмоток по сопротивлению
Когда предварительный анализ обмоток произведен, необходимо убедиться в правильности сделанных выводов, а заодно прозвонить обмотки на отсутствие обрыва. Для этого воспользуемся мультиметром. Если Вы не знаете как измерить сопротивление мультиметром, то прочитайте эту статью.
Вначале прозвоним обычный сетевой трансформатор, у которого всего две обмотки.
Мультиметр переводим в режим «Прозвонка» и производим измерение сопротивления предполагаемых первичной и вторичной обмоток. Здесь все просто: у какой из обмоток величина сопротивления больше, та обмотка и является первичной.
Это объясняется тем, что в маломощных трансформаторах и трансформаторах средней мощности первичная обмотка может содержать 1000…5000 витков, намотанных тонким медным проводом, и при этом может достичь сопротивления до 1,5 кОм. Тогда как вторичная обмотка содержит небольшое количество витков, намотанных толстым проводом, и ее сопротивление может составлять всего несколько десятков ом.
Теперь прозвоним трансформатор, у которого несколько обмоток. Для этого воспользуемся листком бумаги, ручкой и мультиметром. На бумаге будем зарисовывать и записывать величины сопротивлений обмоток.
Делается это так: одним щупом мультиметра садимся на любой крайний вывод, а вторым щупом по очереди касаемся остальных выводов трансформатора и записываем полученное значение сопротивлений.
Выводы, между которыми мультиметр покажет сопротивление, и будут являться выводами одной обмотки. Если обмотка без средних отводов, то сопротивление будет только между двумя выводами.
Если же обмотка имеет один или несколько отводов, то мультиметр покажет сопротивление между всеми этими отводами.
Например. Первичная обмотка может иметь несколько отводов, когда трансформатор рассчитан на работу в сети с напряжениями 110В, 127В и 220В. Вторичная обмотка также может иметь один или несколько отводов, когда хотят от одного трансформатора получить несколько напряжений.
Идем дальше. Когда первая обмотка и ее выводы будут найдены, то переходим к поиску следующей обмотки. Щупом опять садимся на следующий свободный вывод, а другим поочередно касаемся оставшихся выводов и записываем результат. И таким образом производим измерение, пока не будут найдены все обмотки.
Например. Между выводами с номерами 1 и 2 величина сопротивления составила 21 Ом, тогда как между остальными выводами мультиметр показал бесконечность. Из этого следует, что мы нашли обмотку, у которой выводы обозначены номерами 1 и 2. Нарисуем ее так:
Теперь щупом садимся на вывод 3, а другим щупом поочередно касаемся выводов с номерами от 4 до 10. Мультиметр показал сопротивление только между выводами 3, 4 и 5.
Причем между выводами 3 и 4 величина сопротивления составила 6 Ом, а между парой выводов 3, 5 и 4, 5 получилось по 3 Ома. Отсюда делаем вывод, что эта обмотка с отводом посередине, т.е.
пары 3, 5 и 4, 5 намотаны равным количеством витков, и что с этой обмотки снимается два одинаковых напряжения относительно общего вывода 5. Рисуем так:
Производим измерение далее.
Между выводами 6 и 7 величина сопротивления составила 16 Ом. Рисуем так:
Ну и между выводами 9 и 10 сопротивление составило 270 Ом.
А так как среди всех обмоток эта оказалась с самой большой величиной сопротивления, то она и является первичной. Рисуем так:
Вывод 8, к которому припаяна желто-зеленая жилка, ни как не звонился, поэтому смело утверждаем, что это экранирующая обмотка (экран), которую наматывают поверх первичной, чтобы устранить влияние ее магнитного поля на другие обмотки. Как правило, экранирующую обмотку соединяют с корпусом радиоаппаратуры.
В итоге у нас получилось четыре обмотки, из которых одна сетевая и три понижающих. Экранирующая обмотка обозначается пунктирной линией и располагается параллельно с сердечником. И вот на основе полученных результатов нарисуем электрическую схему трансформатора.
Теперь остается подать напряжение на первичную обмотку и измерить выходящие напряжения. Однако тут есть один момент, который необходимо знать, если Вы сомневаетесь в правильности определения первичной (сетевой) обмотки.
Здесь все просто: чтобы не сжечь обмотку трансформатора и ограничить через нее нежелательный ток нужно последовательно с этой обмоткой включить лампу накаливания на напряжение 220В и мощностью 40 – 100 Вт.
Если обмотка определена правильно, то нить накала лампы должна не гореть или еле тлеть.
Если же лампа будет гореть достаточно ярко, то есть вероятность того, что сетевая обмотка трансформатора рассчитана на питающее напряжение 110 — 127В или Вы ее прозвонили неправильно.
Второй момент, по которому можно судить о правильности подключения трансформатора к сети — это сама работа трансформатора. При правильном включении работа трансформатора практически беззвучна и сопровождается слегка ощутимой вибрацией.
Если же он будет громко гудеть и сильно вибрировать, и при этом будет нагреваться обмотка и из нее может пойти дым, то трансформатор однозначно включен неправильно.
В этом случае тут же отключайте трансформатор от сети, чтобы не повредить обмотку.
Однако и тут есть пару нюансов, которые необходимо учитывать, потому как у некоторых трансформаторов каркас с обмотками может неплотно прилегать к сердечнику и от этого работа трансформатора может сопровождаться некоторым гудением и вибрацией, но при этом обмотка греться не будет. В этом случае в зазор между сердечником и каркасом можно вставить кусочек дерева, пластмассы или кусок провода в изоляции и, тем самым, плотно зафиксировать каркас.
Также характерный гул и вибрацию может вызвать плохая стяжка пластин, из которых собран сердечник магнитопровода. Как правило, стягивание сердечника производится металлической скобой, специальными планками, болтами или стяжками, которые обеспечивают необходимую механическую прочность и жесткое соединение деталей сердечника.
Ну вот в принципе и все, что хотел сказать о прозвонке и определению обмоток трансформатора. Если у Вас возникли вопросы по этой теме, то задавайте их в х к статье. Также, в дополнение к статье, можете посмотреть видеоролик.
Удачи!
Как определить мощность трансформатора по сечению сердечника
g84jsm9tB4S
Если на трансформаторе имеется маркировка, то вопрос определения его параметров исчерпывается сам собой, достаточно лишь вбить эти данные в поисковик и мгновенно получить ссылку на документацию для нашего трансформатора. Однако, маркировки может и не быть, тогда нам потребуется самостоятельно эти параметры вычислить.
Для определения номинальных тока и мощности неизвестного трансформатора по его внешнему виду, необходимо в первую очередь понимать, какие физические параметры устройства являются в данном контексте определяющими. А такими параметрами прежде всего выступают: эффективная площадь сечения магнитопровода (сердечника) и площадь сечения проводов первичной и вторичной обмоток.
Речь будем вести об однофазных трансформаторах, магнитопроводы которых изготовлены из трансформаторной стали, и спроектированы специально для работы от сети 220 вольт 50 Гц. Итак, допустим что с материалом сердечника трансформатора нам все ясно. Движемся дальше.
Сердечники бывают трех основных форм: броневой, стержневой, тороидальный. У броневого сердечника эффективной площадью сечения магнитопровода является площадь сечения центрального керна. У стержневого — площадь сечения стержня, ведь именно на нем и расположены обмотки. У тороидального — площадь сечения тела тороида (именно его обвивает каждый из витков).
Для определения эффективной площади сечения, измерьте размеры a и b в сантиметрах, затем перемножьте их — так вы получите значение площади Sс в квадратных сантиметрах.
Суть в том, что от эффективной площади сечения сердечника зависит величина амплитуды магнитного потока, создаваемого обмотками. Магнитный поток Ф включает в себя одним из сомножителей магнитную индукцию В, а вот магнитная индукция как раз и связана с ЭДС в витках. Именно поэтому площадь рабочего сечения сердечника так важна для нахождения мощности.
Далее необходимо найти площадь окна сердечника — того места, где располагаются провода обмоток. В зависимости от площади окна, от того насколько плотно оно заполнено проводниками обмоток, от плотности тока в обмотках — также будет зависеть мощность трансформатора.
Если бы, к примеру, окно было полностью заполнено только проводами обмоток (это невероятный гипотетический пример), то приняв произвольной среднюю плотность тока, умножив ее потом на площадь окна, мы получили бы общий ток в окне магнитопровода, и если бы затем разделили его на 2, а после — умножили на напряжение первичной обмотки — можно было бы сказать, что это и есть мощность трансформатора. Но такой пример невероятен, поэтому нам необходимо оперировать реальными значениями.
Итак, давайте найдем площадь сечения окна.
Наиболее простой способ определить теперь приблизительную мощность трансформатора по магнитопроводу — перемножить площадь эффективного сечения сердечника и площадь его окна (все в кв.см), а затем подставить их в приведенную выше формулу, после чего выразить габаритную мощность Pтр.
В этой формуле: j — плотность тока в А/кв.мм, f — частота тока в обмотках, n – КПД, Вm – амплитуда магнитной индукции в сердечнике, Кс — коэффициент заполнения сердечника сталью, Км — коэффициент заполнения окна магнитопровода медью.
Но мы поступим проще: примем сразу частоту равной 50 Гц, плотность тока j= 3А/кв.мм, КПД = 0,90, максимальную индукцию в сердечнике — ни много ни мало 1,2 Тл, Км = 0,95, Кс=0,35. Тогда формула значительно упростится и примет следующий вид:
Как подключить свечи накала через реле схема
Если же есть потребность узнать оптимальный ток обмоток трансформатора, то задавшись плотностью тока j, скажем теми же 3 А на кв.мм, можно умножить площадь сечения провода обмотки в квадратных миллиметрах на эту плотность тока. Так вы получите оптимальный ток. Или через диаметр провода d обмотки:
Узнав по сечению проводников обмоток оптимальный ток каждой из обмоток, разделите полученную по габаритам мощность трансформатора на каждый из этих токов — так вы узнаете соответствующие найденным параметрам напряжения обмоток.
Одно из этих напряжений окажется близким к 220 вольтам — это с высокой степенью вероятности и будет первичная обмотка. Далее вольтметр вам в помощь. Трансформатор может быть повышающим либо понижающим, поэтому будьте предельно внимательны и аккуратны если решите включить его в сеть.
Кроме того, перед вами может оказаться выходной трансформатор от акустического усилителя. Данные трансформаторы рассчитываются немного иначе чем сетевые, но это уже совсем другая и более глубокая история.
Габаритную мощность трансформатора можно приблизительно узнать по сечению магнитопровода. Правда, ошибка может составлять до 50%, и это связано с рядом факторов.
Габаритная мощность напрямую зависит от конструктивных особенностей магнитопровода, качества и толщины используемой стали, размера окна, величины индукции, сечения провода обмоток и даже качества изоляции между отдельными пластинами.
Чем дешевле трансформатор, тем ниже его относительная габаритная мощность. Конечно, можно путём экспериментов и расчетов определить максимальную мощность трансформатора с высокой точностью, но смысла большого в этом нет, так как при изготовлении трансформатора, всё это уже учтено и отражено в количестве витков первичной обмотки.
- Так что, при определении мощности, можно ориентироваться по площади сечения набора пластин проходящего через каркас или каркасы, если их две штуки.
- P – мощность в Ваттах, B – индукция в Тесла, S – сечение в см²,
- 1,69 – постоянный коэффициент.
Сначала определяем сечение, для чего перемножаем размеры А и Б.
S = 2,5 * 2,5 = 6,25 см²
Затем подставляем размер сечения в формулу и получаем мощность. Индукцию я выбрал 1,5Tc, так как у меня броневой витой магнитопровод.
- P = 1,5 * 6,25² / 1,69 = 35 Ватт
- Если требуется определить необходимую площадь сечения манитопровода исходя из известной мощности, то можно воспользоваться следующей формулой:
- Нужно вычислить сечение броневого штампованного магнитопровода для изготовления трансформатора мощностью 50 Ватт.
- S = ²√ (50 * 1,69 / 1,3) = 8см²
О величине индукции можно справиться в таблице. Не стоит использовать максимальные значения индукции, так как они могут сильно отличаться для магнитопроводов различного качества.
Максимальные ориентировочные значения индукции
| Тип магнитопровода | Магнитная индукция мах (Тл) при мощности трансформатора (Вт) | ||||
| 5-10 | 10-50 | 50-150 | 150-300 | 300-1000 | |
| Броневой штампованный | 1,2 | 1,3 | 1,35 | 1,35 | 1,3 |
| Броневой витой | 1,55 | 1,65 | 1,65 | 1,65 | 1,6 |
| Кольцевой витой | 1,7 | 1,7 | 1,7 | 1,65 | 1,6 |
Как выделить зону коридора
Видео: Как определить мощность трансформатора, несколько способов
- Описание нескольких способов определения мощности 50 Гц трансформаторов.
- Классический теоретический расчет трансформатора достаточно сложен Для его выполнения необходимо знать такие характеристики, как магнитная проницаемость используемых для сердечника пластин трансформаторной стали, длина магнитных силовых линий в сердечнике, средняя длина витка обмотки и другие параметры Профессиональному разработчику НИИ все эти параметры известны, так как он обладает сертификатами применяемых в трансформаторе материалов Радиолюбитель же вынужден использовать для трансформатора совершенно случайно попавший к нему сердечник, характеристики которого ему неизвестны
- По указанной причине для расчета трансформатора предлагается эмпирический метод, многократно проверенный радиолюбителями и основанный на практическом опыте Расчет элементарно прост и требует лишь знания простейших основ арифметикиПринцип действия трансформатора
- Рис 61 Трансформатор: а – общий вид б – условное обозначение
- Трансформатор был изобретен П Н Яблочковым в 1876 году Устройство трансформатора показано на рис 61а, а его схематическое обозначение – на рис 616
- Трансформатор состоит из стального сердечника и обмоток, намотанных изолированным обмоточным проводом
- Сердечник собирается из тонких пластин специальной электротехнической стали для снижения потерь энергии
- Обмотка, предназначенная для подключения к сети переменного тока, называется первичной Нагрузка подключается к вторичной обмотке, которых в трансформаторе может быть несколько Номера обмоток обычно проставляются римскими цифрами Часто обмоткам присваивают номера их выводов
- Работа трансформатора основана на магнитном свойстве электрического тока При подключении концов первичной обмотки к электросети по этой обмотке протекает переменный ток, который создает вокруг ее витков и в сердечнике трансформатора переменное магнитное поле Пронизывая витки вторичной обмотки, переменное магнитное поле индуцирует в них ЭДС Соотношение количества витков первичной и вторичной обмоток определяет получаемое напряжение на выходе трансформатора Если количество витков вторичной обмотки больше, чем первичной, выходное напряжение трансформатора будет больше напряжения сети Такая обмотка называется повышающей Если же вторичная обмотка содержит меньше витков, чем первичная, выходное напряжение окажется меньше сетевого (понижающая обмотка)
- Трансформатор – это пассивный преобразователь энергии Его коэффициент полезного действия (КПД) всегда меньше единицы Это означает, что мощность, потребляемая нагрузкой, которая подключена к вторичной обмотке трансформатора, меньше, чем мощность, потребляемая нагруженным трансформатором от сети Известно, что мощность равна произведению силы тока на напряжение, следовательно, в повышающих обмотках сила тока меньше, а в понижающих – больше силы тока, потребляемого трансформатором от сети
- Параметры и характеристики трансформатора
- Два разных трансформатора при одинаковом напряжении сети могут быть рассчитаны на получение одинаковых напряжений вторичных обмоток Но если нагрузка первого трансформатора потребляет большой ток, а второго – маленький, значит, первый трансформатор характеризуется по сравнению со вторым большей мощностью Чем больше сила тока в обмотках трансформатора, тем больше и магнитный поток в его сердечнике, поэтому сердечник должен быть толще Кроме того, чем больше сила тока в обмотке, тем более толстым проводом она должна быть намотана, а это требует увеличения окна сердечника Поэтому габариты трансформатора зависят от его мощности И наоборот, сердечник определенного размера пригоден для изготовления трансформатора только до определенной мощности, которая называется габаритной мощностью трансформатора
Как почистить турку внутри
- Количество витков вторичной обмотки трансформатора определяет напряжение на ее выводах Но это напряжение зависит также и от количества витков первичной обмотки При определенном значении напряжения питания первичной обмотки напряжение вторичной зависит от отношения количества витков вторичной обмотки к количеству витков первичной Это отношение и называется коэффициентом трансформации
- Если напряжение на вторичной обмотке зависит от коэффициента трансформации, можно ли выбирать количество витков одной из обмоток, например первичной, произвольно Оказывается, нельзя Дело в том, что чем меньше габариты сердечника, тем больше должно быть количество витков каждой обмотки Поэтому размеру сердечника трансформатора соответствует вполне определенное количество витков его обмоток, приходящееся на один вольт напряжения, меньше которого брать нельзя Эта характеристика называется количеством витков на один вольт
- Как и всякий преобразователь энергии, трансформатор обладает коэффициентом полезного действия – отношением мощности, потребляемой нагрузкой трансформатора, к мощности, которую нагруженный трансформатор потребляет от сети
- КПД маломощных трансформаторов, которые обычно применяются для питания бытовой электронной аппаратуры, колеблется в пределах от 0,8 до 0,95 Более высокие значения имеют трансформаторы большей мощности
- Электрический расчет трансформатора
- Прежде чем начать электрический расчет силового трансформатора, необходимо сформулировать требования, которым он должен удовлетворять Они и будут являться исходными данными для расчета Технические требования к трансформатору определяются также путем расчета, в результате которого определяются те напряжения и токи, которые должны быть обеспечены вторичными обмотками Поэтому перед расчетом трансформатора производится расчет выпрямителя для определения напряжений каждой из вторичных обмоток и потребляемых от этих обмоток токов Если же напряжения и токи каждой из обмоток трансформатора уже известны, то они и являются техническими требованиями к трансформатору
- Для определения габаритной мощности трансформатора необходимо определить мощности, потребляемые от каждой вторичной обмотки, и сложить их, учитывая также КПД трансформатора Мощность, потребляемую от любой обмотки, определяют умножением напряжения между выводами этой обмотки на силу потребляемого от нее тока:
- где Р – мощность, потребляемая от обмотки, Вт
- U – эффективное значение напряжения, снимаемого с этой обмотки, В
- I – эффективное значение силы тока, протекающего в этой же обмотке, А
- Суммарная мощность, потребляемая, например, тремя вторичными обмотками, вычисляется по формуле:
- Для определения габаритной мощности трансформатора полученное значение суммарной мощности Ps нужно разделить на КПД трансформатора:
- где Рг – габаритная мощность трансформатора
- η – КПД трансформатора
- Заранее рассчитать КПД трансформатора нельзя, так как для этого нужно знать величину потерь энергии в обмотках и в сердечнике, которые зависят от параметров самих обмоток (диаметры проводов и их длина) и параметров сердечника (длина магнитной силовой линии и марка стали) И те и другие параметры становятся известны только после расчета трансформатора Поэтому с достаточной для практического расчета точностью КПД трансформатора можно определить из табл 61
Как считать электрическую мощность?
Чтобы обеспечить нормальное функционирование электрической проводки, необходимо ещё на этапе проектирования правильно рассчитать мощность, подобрать кабель подходящего сечения. От этого зависит не только срок эксплуатации системы, но и пожаробезопасность сооружения. Если выбрать сечение ошибочно или неправильно рассчитать мощность, можно столкнуться с такими опасными последствиями, как возгорание электропроводки, короткие замыкания, пожар и пр. При выборе оборудования и кабельно-проводниковой продукции важно учитывать разные критерии, среди которых напряжение, сила тока, особенности эксплуатации сети.
Формула расчёта
В уже функционирующей сети измерить мощность электрического тока можно при помощи специального оборудования. Что же делать на этапе проектирования? Ведь самой цепи ещё нет. В этом случае применяется расчётный метод.
Существует два вида мощности: активная и реактивная. Активная превращается в полезную энергию безвозвратно, считается полезной. Реактивная предусматривает затрату определенного (расчетного согласно установленного оборудования и типа оборудования) количества энергии.
В нашем случае реактивная мощность нам не интересна, и мы не будем ее рассчитывать!
В цепях переменного тока, ток и напряжения сдвигаются относительно друг друга.
Этот сдвиг на угол cos обозначается буквой φ (фи).
При расчёте мощности электрической мощности следует учитывать тип сети:
P=U*I*cosφ — для однофазной;
P=√3*U*I*cosφ — для трехфазной.
U – это напряжение сети,
I – сила тока,
cosφ – коэффициент мощности.
cosφ – коэффициент мощности, это паспортная величина оборудования, если не известно о типе оборудования (например, квартиры), то cosφ – расчетный и берется из инструкции по проектированию (СП 256.1325800.2016)
Зависимость коэффициента мощности
Чтобы рассчитать полную (Обращаем внимание, что имеется ввиду установленная, т.е. полная мощность) мощность, необходимо определить суммарную мощность всей техники и оборудования, которые будут эксплуатироваться, и подключаться к данной электрической сети. Это можно узнать путём суммирования мощностей приборов (этот показатель указан в паспорте товара).
При определении коэффициента мощности учитывается характер нагрузки. К примеру, для нагревательного оборудования он близится к 1. Важно учитывать, что любая активная нагрузка предполагает незначительную реактивную составляющую, поэтому коэффициент мощности будет равен не 1, а 0,95. Для более мощных приборов – 0,8. Напряжение для однофазных цепей принимается 220 В, для трехфазных – 380 В.
Почему мощность нельзя измерить мультиметром: ammo1 — LiveJournal
Многие авторы обзоров светодиодных ламп делают ошибку, пытаясь измерить потребляемую мощность мультиметром.
Как известно, значение электрической мощности можно получить, умножив значения напряжения и силы тока. Поэтому кажется, что достаточно измерить напряжение и ток мультиметром и их перемножить.
Но не всё так просто.
Точнее, для постоянного тока всё просто и мультиметр вполне подойдёт для измерения мощности, а вот для переменного тока всё зависит от нагрузки. Пока нагрузка резистивная (например обычная лампа накаливания или нагревательный прибор), её потребление энергии постоянно. В этом случае мультиметр покажет средний ток и действующее напряжение. Перемножаем — получаем мощность.
В большинстве современных электроприборов (включая светодиодные лампы) используются электронные преобразователи напряжения, потребление которых обычно выглядит так.
Если измерить потребляемый ток такой нагрузки обычным мультиметром и умножить на сетевое напряжение получится значение, не имеющее ничего общего с реальной потребляемой мощностью. Дорогие TrueRMS-мультиметры честно измеряют среднеквадратичные значения напряжения и тока даже в самых странных случаях, но их перемножение даёт полную мощность, а нас интересует активная. Дело в том, что все бытовые электросчётчики считают только активную мощность и производители указывают для своей продукции также активную мощность. За реактивную мощность мы не только не платим, но она и не превращается в работу в устройстве и возвращается обратно в сеть, поэтому её нельзя учитывать при расчёте КПД устройства.
В принципе, если знать коэффициент мощности (Power Factor, PF) устройства, можно получить активную мощность, умножив полную мощность на PF.
У некоторых устройств (в данном случае это светодиодные лампы) потребление принимает вот такие причудливые формы.
Для измерения мощности устройств, работающих от сети, выпускаются сетевые измерители мощности.
Такой измеритель много раз в секунду измеряет мгновенные значения напряжения и тока, перемножает их и вычисляет среднее значение мощности. Только так можно узнать реальную мощность, потребляемую электроприбором от сети. Многие из таких измерителей, показывают и Power Factor.
p.s. Спасибо Олегу Артамонову за технические консультации. Подробно о видах мощности и измерении энергопотребления читайте в его статье: http://fcenter.ru/online/hardarticles/tower/6484#2.
© 2016, Алексей Надёжин
Основная тема моего блога — техника в жизни человека. Я пишу обзоры, делюсь опытом, рассказываю о всяких интересных штуках. А ещё я делаю репортажи из интересных мест и рассказываю об интересных событиях.
Добавьте меня в друзья здесь. Запомните короткие адреса моего блога: Блог1.рф и Blog1rf.ru.
Второй мой проект — lamptest.ru. Я тестирую светодиодные лампы и помогаю разобраться, какие из них хорошие, а какие не очень.
Как измерить силу тока мультиметром
Очень хорошо, когда в инструментальном «арсенале» владельца дома или квартиры имеются контрольно-измерительные приборы. В частности если речь идет об электрохозяйстве, нередко приходится прибегать к помощи мультиметра. Этот компактный и относительно недорогой по нынешним временам прибор позволяет тестировать бытовую технику и освещение, выявлять неполадки в домашней электрической сети, контролировать уровень заряда батареек и аккумуляторов, становится незаменимым при различных электромонтажных работах.
Как измерить силу тока мультиметром
Но кроме наличия самого мультиметра, необходимо еще и умение работать с ним. Вот здесь бывает сложнее. Если, скажем, с прозвоном провода, определением наличия и величины напряжения обычно проблем не возникает, то с замером силы тока у многих возникают неясности. И, кстати, эта операция, по сравнению с другими упомянутыми, наиболее сложна и в определенных условиях бывает наиболее опасна.
Поэтому темой предлагаемой публикации станет вопрос, как измерить силу тока мультиметром.
Несколько слов о силе тока, и для чего ее бывает нужно измерять
Для начала вспомним, что же это такое – сила электрического тока.
Этот показатель (I) измеряется в амперах и входит в число основных физических величин, определяющих параметры той или иной электрической цепи. К двум другим относят напряжение (U, измеряется в вольтах) и сопротивление нагрузки (R, измеряется в омах).
Как преподносилось в школьном курсе физики, электрический ток является направленным движением заряженных частиц по проводнику. Если рассматривать с большим упрощением, вызывается он электродвижущей силой, возникающей из-за разности потенциалов (напряжения) на полюсах (клеммах, контактах) подключенного источника питания. По своей сути сила тока показывает количество этих самых заряженных частиц, проходящих через конкретную точку (элемент схемы) в единицу времени (секунду).
На величину силу тока в цепи влияют два других параметра. Напряжение связано прямой пропорциональностью – так, например, его увеличение вызывает и повышение силы тока. Сопротивление – наоборот, то есть с его ростом при том же напряжении сила тока снижается.
Забавная картинка, наглядно демонстрирующая взаимосвязь основных величин электрической цепи: «Вольт стремится «пропихнуть» Ампер по проводнику, преодолевая препятствия, чинимые Омом».
А слева на иллюстрации показано графическое, удобное для восприятия, изображение закона Ома, показывающего эти взаимосвязи. Из этой «пирамиды» легко составляются формулы в их привычном написании:
U = I × R
I = U / R
R = U / I
Итак, сила тока измеряется в амперах. С некоторым упрощением можно объяснить так, что 1 ампер – это ток, который возникнет в проводнике сопротивлением 1 ом, если к нему приложить напряжение, равное одному вольту.
Кроме основной единицы, используют и производные. Так, довольно часто приходится иметь дело с миллиамперами. Из самого термина понятно, что 1 мА = 0.001 А.
Кстати, сразу упомянем, и про мощность. Ток в 1 ампер, вызванный напряжением 1 вольт, выполнит работу в 1 джоуль. А если это привести к единице времени (секунде), то получится значение мощности, равное 1 ватту.
Это определяется формулой закона Джоуля-Ленца:
P = U × I
где Р – мощность, выраженная в ваттах.
Для чего все это рассказывалось? Да просто потому, что большинство случаев замера силы тока, так сказать, на бытовом уровне, так или иначе связано с определением других параметров. Согласитесь, мало кому придет в голову мысль: «а дай-ка я проверю силу тока просто так», то есть без дальнейшего практического приложения. Тем более что, как уже упоминалось выше, работа с амперметром – наиболее сложная и зачастую небезопасная.
Например, в каких случаях чаще всего замеряют силу тока:
- Для уточнения реальной потребляемой мощности того или иного бытового электроприбора. Промерив значения силы тока и напряжения несложно по формуле вычислить и мощность.
- Этот же промер и последующий расчет позволяют оценить, советует ли подводимая линия питания таким нагрузкам.
- Случается, что подобные «ревизии» позволяют выявить пока еще скрытые, незамеченные дефекты прибора – когда значение силы тока (и мощности, соответственно) намного отличаются от заявленного в паспорте номинала в ту или иную сторону.
- Измерения силы тока позволяют оценить степень заряженности автономных источников питания – аккумуляторов и батареек. Проверка их по напряжению никогда не дает объективной картины. Вольтметр может показать, скажем, положенные 1.5 вольта, но уже спустя несколько минут элемент питания безнадежно «сядет». То есть проверку следует проводить именно измерением силы тока.
- Таким измерением можно выявить утечку тока, там, где ее по идее быть не должно. Это часто практикуется автомобилистами, если у них есть подозрения, что аккумулятор слишком активно разряжается, когда машина «отдыхает» в гараже или на стоянке. Проведенная проверка позволяет локализовать участок утечки и избежать, кстати, немалых проблем, к которым она может привести.
Цены на мультиметры
мультиметр
Умение замерять силу тока позволяет выявить утечку в электрохозяйстве автомобиля
- Иногда требует проверки зарядное устройство аккумулятора – выдает ли оно необходимое значение тока зарядки.
Возможны и иные случаи, когда требуется иметь объективные данные о реальной силе тока. Но основные случаи все же перечислены.
Разбираемся с устройством мультиметра
Для измерения силы тока используются специальные приборы, название которых говорит само за себя – амперметры. В продаже чаще всего встречаются амперметры стационарной установки, в виде панелек или для DIN-рейки. Они обычно монтируются в распределительном щите и позволяют отслеживать текущие показатели силы тока, например, за всю локальную систему электроснабжения или на какой-то выделенной её линии.
Амперметры стационарной установки – панельного типа (слева) и для монтажа в распределительный щит на DIN-рейку
Устанавливают такие приборы, если в этом есть необходимость, только специалисты электрики. Измерить силу протекающего тока с помощью них – проще простого. Необходимо просто взглянуть на текущие показания при включенной на линии нагрузке.
Этим, по сути, их функциональность и ограничивается. Естественно, у хозяина квартиры (дома) не будет возможности снять подобный прибор с места его стационарной установки для проведения замеров в другом месте.
Другой вариант, который уже позволяет работать в нужном месте – это так называемый лабораторный амперметр. Настольный прибор, в котором имеются клеммы, то есть предусмотрена возможность подключения измерительных проводов со щупами для проверки силы тока на том или ином участке цепи.
Лабораторный амперметр – ограниченность в функциональных возможностях делает такие приборы невостребованными для домашнего хозяйства.
Но приобретать такой «девайс» для домашнего инструментального «арсенала» — вряд ли имеет смысл. Просто по той причине, что замером силы тока все и ограничивается. А это измерение, кстати, как уже говорилось, проводится на «бытовом» уровне, пожалуй, реже всего.
Поэтому такие приборы популярности себе не снискали. И оптимальным вариантом является мультитестер (мультиметр).
Эти измерительные многофункциональные приборы представлены в продаже в очень большом разнообразии. Первое, сразу бросающееся в глаза различие – приборы могут быть стрелочными, со снятием показаний со шкал. Несмотря на то что считаются уже «вчерашним днем», некоторые мастера отдают предпочтение именно им. Но для новичка может быть затруднительно на первых порах считывать показания – со шкалами и шагом из градуировки по неопытности несложно запутаться.
«Дисплей» некогда очень популярного мультиметра Ц4353. Одна стрелка и множество шкал, с которыми начинающему бывает непросто разобраться.
Поэтому максимальной популярностью пользуются все же цифровые мультиметры, демонстрирующие на дисплее показания в абсолютном выражении. Умение пользоваться такими приборами приобретается гораздо быстрее. Стоимость многих моделей – весьма доступная, и подобные мультитестеры прочно вошли в домашний инструментальный набор.
Но и среди них бывают существенные различия, которые необходимо знать и учитывать при проведении измерения электрических параметров.
Наиболее удобны, наверное, мультиметры, в которых достаточно выставить лишь режим измерений. Допустимый диапазон при этом не указывается – прибор автоматически подстроится под параметры цепи, проведет замер и выдаст искомый результат.
Цены на мультиметр Ц4353
мультиметр Ц4353
Пример показан на иллюстрации:
Удобный в пользовании мультитестер, в котором упрощена установка режимов работы
Рукоятка переключателя режимов (поз.1) имеет всего несколько положений. Это напряжение – объединено переменное V AC (значок ~) и постоянное DC (—), в вольтовом и милливольтом диапазоне. Аналогично и с силой тока – А, тоже без разделения на тип тока, но с градацией на амперы и миллиамперы. Кроме того, обязательно имеется опция замера сопротивления и прозвона цепи. Могут быть и другие заложенные функции.
В нижней части расположены гнезда для подключения измерительных проводов со щупами. Их бывает три или четыре. Обязательно имеется гнездо СОМ – для «общего» провода (поз. 2), как правило – черного цвета. Гнездо поз. 3 – для красного провода при проведении подавляющего большинства измерений. Под гнездом имеется надпись с указанием допустимых пределов измерений по напряжению и току. И, наконец, гнездо поз. 4 – выделено для замеров силы тока, исчисляемой в амперах. Также указан допустимый предел — не более 10 А.
Показания высвечиваются на цифровом дисплее (поз. 5).
Такие приборы удобны, однако их стоимость в несколько раз превышает цену на широкодоступные мультиметры. Поэтому их чаще можно увидеть у профессионалов.
Более распространенный вариант – мультиметры, при пользовании которыми необходимо не только переключать режим и переставлять измерительные провода, но еще и указывать предполагаемый диапазон измерений.
К установке положения переключателя в таком мультитестере приходится относиться более внимательно
При пользовании таким мультиметром требуется не только указать режим работы, но и выставит переменный или постоянный ток. И уже в этом секторе установить переключатель в предполагаемый диапазон измерений, выраженный в миллиамперах мА (бывает еще и в микроамперах, µА) или в амперах А.
Аналогично дело обстоит и с режимами замера напряжения.
Еще нюанс – показан пример с четырьмя гнездами подключения проводов. Здесь для измерения силы тока для красного провода выделено два гнезда. Одно – с токами до 200 мА, второе – до 10 А. Все остальные замеры (напряжения, сопротивления, емкости и другие) проводятся через отдельное гнездо.
Но обычно под этими гнездами-клеммами располагается понятная схема, позволяющая избежать ошибок. Просто надо быть внимательным.
А теперь – еще один очень важный нюанс. Показанные выше приборы позволяют проводить замер силы тока как постоянного, так и переменного. Но очень часто обычными пользователями приобретаются мультиметры с «усеченными» возможностями. Такие приборы широко популярны из-за своей супердоступной цены. И некоторые потенциальные владельцы не обращают внимание на этот их недостаток.
Так, наиболее распространенными на бытовом уровне являются мультитестеры типа DT830 или DT832. Они позволяют выполнить бо́льшую часть возможных измерений. Но, обратите внимание, функции амперметра для переменного тока у них НЕ ПРЕДУСМОТРЕНА.
Очень широко распространенная модель мультитестера DT830. Привлекает и ценой, и довольно большими возможностями. Но измерения силы переменного тока в ней не предусмотрено.
Таким образом, если есть необходимость проверить силу тока в цепи работающего от сети 220 В/50 Гц бытового прибора, то просто так это не получится. Потребуется искать другой, более совершенный мультиметр. Или придумывать дополнительные «усовершенствования», которые позволят обойтись и таким тестером. Об этом будет сказано ниже.
Основные принципы замера силы тока
Главной особенностью работы с мультитестером в режиме амперметра является то, что он обязательно должен быть включен в разрыв цепи. Такое подключение называется последовательным. По сути, прибор становится частью этой цепи, то есть весь ток должен пройти именно через него. А как известно, сила тока на любом участке неразветвленной электрической цепи постоянна. Проще говоря, сколько «вошло» столько должной и «выйти». То есть место последовательного подключения амперметра особого значения не имеет.
Чтобы стало понятнее, ниже размещена схема, в которой показывается разница в подключении мультиметра в разных режимах работы.
Различия в принципах подключения мультитестера в разных режимах измерений
- Итак, при замере силы тока мультиметр включается в разрыв цепи, сам становясь одним из ее звеньев. То есть будет проблема, как этот разрыв цепи организовать практически. Решают по-разному – это будет показано ниже.
- При замере напряжения (в режиме вольтметра) цепь, наоборот, не разрывается, а прибор подключается параллельно нагрузке (участку цепи, где требуется узнать напряжение). При замере напряжения источника питания щупы подключаются напрямую к клеммам (контактам розетки), то есть мультиметр сам становится нагрузкой.
- Наконец, если меряется сопротивление, то внешний источник питания вообще не фигурирует. Контакты прибора подключаются непосредственно к той или иной нагрузке (прозваниваемому участку цепи). Необходимый ток для проведения измерений поступает из автономного источника питания мультитестера.
Вернемся к теме статьи — к замерам силы тока.
Очень важно изначально правильно установить на мультиметре, помимо постоянного или переменного тока, диапазон измерений. Надо сказать, что у начинающих с этим часто возникают проблемы. Сила тока – величина крайне обманчивая. И «спалить» свой прибор, а то и наделать больших бед, неправильно установив верхний предел измерений – проще простого.
Начинать измерения силы тока, особенно если нет представления о возможной его величине в цепи, следует с максимального диапазона мультитестера. При необходимости можно, переставив провод и последовательно снижая верхний предел, выйти на оптимальный.
Поэтому настоятельная рекомендация – если вы не знаете, какая сила тока ожидается в цепи, начинайте измерения всегда с максимальных величин. То есть, например, на том же DT 830 красный щуп должен быть установлен в гнездо на 10 ампер (показано на иллюстрации красной стрелкой). И рукоятка переключатель режимов работы также должно показывать на 10 ампер (голубая стрелка). Если измерения покажут, что предел завышен (показания получаются менее 0,2 А), то можно, чтобы получить более точные значения, переставить сначала красный провод в среднее гнездо, а затем ручку переключателя – в положение 200 мА. Бывает, что и этого многовато, и приходится переключателем снижать еще на разряд и т.д. Не вполне удобно, не спорим, но зато безопасно и для пользователя, и для прибора.
Кстати, о безопасности. Никогда не следует пренебрегать мерами предосторожности. И особенно если речь идет об опасных напряжениях (а сетевое напряжение 220 В – чрезвычайно опасно) и высоких токах.
Мы здесь спокойно ведём разговор об амперах, а между тем, безопасным для человека считается ток не выше 0.001 ампера. А ток всего в 0.01 ампера, прошедший через тело человека, чаще всего приводит к необратимыми последствиям.
Что важно знать об опасности электрического тока
Электричество – это величайший помощник человечества. Но при неграмотном, беспечном или откровенно наплевательском отношении к соблюдению безопасности – карает мгновенно и беспощадно. Что необходимо накрепко запомнить об опасности электрического тока, прежде чем приступать к любым электромонтажным работам – читайте в специальной публикации нашего портала.
Проведение замеров силы тока, особенно если работа ведется в самом высоком диапазоне, рекомендуется проводить максимально быстро. В противном случае мультитестер может просто перегореть.
Об этом, кстати, могут информировать и предупреждающие надписи около гнезда подключения измерительного провода.
Пример предупреждающей надписи у гнезда подключения провода для замеров на максимально допустимом диапазоне токов
Обратите внимание. Слово «unfused» в данном случае обозначает, что прибор в этом режиме не защищен плавким предохранителем. То есть при перегреве он просто выйдет полностью из строя. Указано и допустимое время замера – не более 10 секунд, да и то не чаще одного раза в 15 минут («each 15 m»). То есть после каждого такого замера придется еще и выдерживать немалую паузу.
Справедливости ради – далеко не все мультиметры настолько «привередливые». Но если такое предупреждение есть – пренебрегать им не стоит. И в любом случае замер силы тока проводить максимально быстро.
Как проводится измерение силы тока
В этом разделе статьи рассмотрим несколько наиболее характерных случаев.
И для начала ответим на один почему-то весьма часто задаваемый, и при этом – совершенно безграмотный вопрос.
Как измерить силу тока в розетке?
Ответ категоричный – НИКАК!
Никакого тока в розетке не ищите – там есть только напряжение на контактах, между фазой и нулем. А ток возникнет лишь тогда, когда к розетке будет подключена нагрузка – неважно что это, лампочка накаливания или бытовой прибор. Естественно, рассчитанный на работу с сетевым напряжением 220 вольт.
А что будет, если в режиме амперметра все же вставить щупы мультитестера в розетку? Да все произойдет очень просто и быстро. Собственное сопротивление прибора – невелико, то есть практически гарантированно получается короткое замыкание. Вспомните закон Ома – при стремящемся к нулю сопротивлении сила тока возрастает до огромных значений. Хорошо, если все ограничится срабатыванием защиты и перегоранием плавкого предохранителя в мультитестере. Если он «unfused», о чем говорилось выше – гарантированное перегорание, и прибор нередко остается только выбрасывать. И это еще в лучшем случае – иногда бывают и «фейерверки».
Запомните «золотую истину» – пока к розетке ничего не подключено, ток в ней однозначно равен нулю. И проверять это экспериментально – себе дороже!
А вот замер силы тока в цепи подключённого к розетке бытового прибора – это уже совсем другой случай.
Как измерить силу тока в цепи подключенного бытового прибора
Нельзя сказать, что подобная проверка проводится часто, но иногда она помогает разобраться с правильностью организации домашней электросети. То есть сопоставить соответствие реальной силы тока подведенным к розетке проводам и возможностям другого электротехнического оборудования. Или же дает возможность проверить реальную потребляемую мощность бытового прибора. Если она сильно отличается от паспортной в ту или иную сторону, это может говорить о пока еще не выявленной неисправности.
Схема в общих чертах выглядит следующим образом
Принципиальная схема замера силы тока в цепи подключенного бытового прибора
1 – розетка 220 вольт.
2 – условно – бытовой прибор.
3 – кабель питания прибора.
4 – точки разрыва цепи (подсоединения щупов тестера). В данном случае они показаны на фазном проводе, хотя для проверки силы переменного тока это не имеет никакого значения — могут быть и на нулевом.
5 – мультиметр, установленный в режим измерения переменного тока 10 А
6 – измерительные провода мультитестера.
Все просто – после сборки такой схемы необходимо подсоединить кабель питания к розетке, а затем запустить бытовой прибор в нужном режиме выключателем. И спустя 3÷5 секунд (некоторым приборам требуется время для выхода на номинальный режим) снять показания силы тока в амперах.
Но как это осуществить, так сказать, технологически? Резать изоляцию и затем – один из проводов кабеля питания, чтобы подключить в разрыв амперметр? Иногда поступают и так. Пример показан на иллюстрации.
Согласитесь, не слишком привлекательный вариант. Нарушается целостность внешней оплетки провода. Концы придется после замеров сращивать и изолировать. Для разовой срочной проверки – может, и сгодится, но не более того.
Городить дополнительные провода между розеткой и вилкой, чтобы «вклинить» между ними амперметр? Тоже довольно неудобно.
Чтобы замеры были безопасными, а их проведение занимало минимум времени и усилий, можно изготовить специальное приспособление. Для этого потребуется небольшая фанерная площадка, две накладные (внешние) розетки (самые дешевые) и отрезок сетевого шнура с вилкой.
Схематично этот «испытательный стенд» будет выглядеть так:
Несложное в изготовлении приспособление для удобного и безопасного замера силы тока
На небольшом жестком фрагменте (поз. 1) например, фанерном, текстолитовом и т.п., крепятся две розетки, так, как показано на схеме. Розетки совершенно условно пронумеруем №1 и №2, а их контакты назовем соответственно 1а и 1б, 2а и 2б.
К розеткам поводится сетевой шнур (поз.4) с вилкой (поз.3). Эта вилка будет подключаться в обычную сетевую розетку.
Шнур разделан, и два его провода подключены к клеммам одноимённых контактов обеих розеток. То есть на схеме это 1а и 2а. А вторая пара, 1б и 2б контактов соединена перемычкой из одножильного провода.
Как проводить замеры с таким приспособлением?
- Для начала – витка сетевого шнура подключается к розетке (к любой или к тестируемой, то есть к той, к которой подключается на постоянной основе испытываемый бытовой прибор). Вся конструкция у нас после сборки полностью закрыта, изолирована, никаких открытых токопроводящих деталей нет.
- Имеет смысл для начала проверить напряжение в розетке. Если конечной целью ставится определение реальной мощности прибора, то этот параметр желательно уточнить. Иногда, если домашняя сеть не имеет стабилизатора, он значительно отличается от заявляемых 220 вольт. То есть это может повлиять на конечный результат.
Проверить напряжение несложно. Мультиметр переключается в режим ~V (ACV) с диапазоном больше 220 вольт (обычно это 750 вольт). Штекера проводов устанавливаются в соответствующие гнезда прибора (СОМ и ~V). Затем щупы прибора вставляются в контакты розеток 1а и 2а, как показано на схеме ниже.
Первый рекомендуемый замер – напряжение в сети.
- После этого в одну розетку (любую) вставляется вилка сетевого шнура испытываемого прибора. Цепь не замкнута – разрыв ее получается на второй розетке.
- Мультитестер переводится в режим амперметра переменного тока (~A или ACA) в максимальный диапазон. Штекер красного измерительного провода переставляется в соответствующий разъем.
Конечная схема подключения нагрузки и мультитестера в испытательном приспособлении
- После этого щупы мультитестера вставляются в гнезда оставшейся свободной розетки. И теперь осталось только включить испытываемый бытовой прибор и снять с мультитестера показания силы тока.
Все исходные данные есть – можно рассчитать потребляемую мощность прибора на момент замера. Можно воспользоваться расположенным ниже калькулятором:
Калькулятор расчета мощности электроприбора
Перейти к расчётам
Как видите, и довольно сложную задачу замера силы тока питания бытового прибора вполне можно решить с должным уровнем безопасности и комфорта.
А что делать, если мультитестер не рассчитан на измерение силы переменного тока?
Бывает, что требуется измерить силу переменного тока, примерно так, как показывалось выше. но в распоряжении лишь мультиметр, не рассчитанный на такую операцию. И приобретать новый – нет желания или возможности. Если ли выход?
Да, можно выполнить замер и в такой ситуации. Существует для этого несколько способов. Но в любом случае придётся сначала провести некоторые подготовительные работы.
Измерение силы переменного тока с помощью вольтметра и дополнительного сопротивления.
Да, это совершенно серьезно, именно с помощью вольтметра. Снова вспомним закон Ома для участка электрической цепи:
I = U / R
Но если сопротивление на этом участке будет равно ровно одному ому, то получается, что номиналы силы тока и напряжения – совпадут.
I (A) = U(V) / 1 = U(V)
Значит, задача состоит в том, чтобы в разрыв цепи поместить резистор номиналом ровно в 1 ом, а затем промерить напряжение на его концах.
Талой резистор можно приобрести в магазине. Правда, не забываем, что на нем будет потребляться весьма внушительная мощность, и лучше приобретать керамический резистор на 10 или даже 50 Вт.
Керамический резистор номиналом 1 ом / 50 ватт
Правда, такие резисторы далеко не всегда есть в продаже. Да и стоить они могут немало. Можно обойтись и самодельным, накрутив спираль из нихромовой проволоки.
В интернете полно таблиц с удельными сопротивлениями нихромовых проводников различных диаметров. То есть провести расчет требуемой длины, чтобы «выскочить» на 1 ом – не столь сложно.
Например, будет использоваться нихромовая проволока диаметром 0,4 мм (сечение 0,123 мм²). Ее удельное сопротивление составляет 7,94 Ом/м. Несложно рассчитать, что для сопротивления 1 ом потребуется 126 мм проволоки.
Из проволоки можно просто намотать спираль, но лучше выполнить ее на небольшом стеклотекстолитовом каркасе и сделать удобные контакты.
Из этого отрезка навивается спираль. Или, что еще удобнее и безопаснее – можно намотать проволоку на панельку их стеклотекстолита, как показано на иллюстрации. После намотки проводят проверку мультиметром в режиме омметра. При необходимости – корректируют длину, чтобы сопротивление было 1 ом с максимально возможной точностью.
Ознакомьтесь с назначением и приемами работы с мегаомметром, из нашей новой статьи на нашем портале — «Как пользоваться мегаомметром».
Концы резистора можно прикрепить, например, к штырям разобранной вилки – чтобы удобнее было их подключать к разрыву цепи.
Если резистор готов, можно приниматься за измерения.
Цены на мультитестеры
мультитестер
Самодельный резистор сопротивлением 1 ом установлен в разрыв цепи. Замерив на нем переменное напряжение, одновременно получим и точное значение силы тока.
В свободную розетку к ее контактам присоединяют самодельный резистор. После этого можно сразу к его концам «крокодильчиками» подцепить щупы мультиметра. Провода и сам тестер должны быть настроены на режим вольтметра для переменного тока.
Включается прибор-нагрузка. Но дисплее мультиметра показывается напряжение (в вольтах) для участка цепи сопротивлением 1 ом . Это же значение, но только в амперах – искомая сила тока в замкнутой цепи.
Важно – резистор при таком замере может очень быстро нагреваться, буквально докрасна. Поэтому снятие показаний должно выполняться с максимальной оперативностью. Как только подключенный прибор вышел на свою мощность, показания на дисплее стабилизировались – их записывают и выключают нагрузку.
Есть и другой способ измерения силы переменного тока при отсутствии соответствующего амперметра. Ток можно выпрямить с помощью диодного моста. Подробнее об этом – в предлагаемом видеосюжете.
Видео: Как можно переделать амперметр постоянного тока под переменный
Как с помощью амперметра можно проверить элементы питания
Еще один частый случай, когда приходится переключать мультитестер в режим измерения силы тока. Речь идет о проверке элементов питания. Помогает как при приобретении батареек в сомнительных торговых точках, так и при ревизии накопившегося дома запаса.
Безусловно, для начала будет неплохо проверить батарейки по напряжению. Для этого переключатель режимов мультиметра устанавливается на постоянное напряжение (DCV). Предел измерений – в соответствии с заявляемым напряжением элемента питания. Если это наиболее распространенные 1.5 вольта, то оптимальным будет предел 2000 мВ (= 2В). Можно установить и 20 В – в этот предел вкладываются практически все используемые элементы питания.
Щуп черного провода (СОМ) прикладывается к отрицательному полюсу элемента питания. Красный, установленный в соответствующее гнездо – к положительному. Производится быстрый замер напряжения. И если оно менее 1.2 В, то такую батарейку можно смело отправлять на утилизацию – она села, и чудес от нее ждать не приходится.
Для этой батарейки все проверки уже закончены замером напряжения – с таким показателем ее ждет только утилизация
Кстати, о полярности. При работе с переменным током, ясное дело, это не имеет значения. А при замерах постоянного напряжения или тока ее соблюдение важно для стрелочных мультиметров. Если щупы расположены неправильно – стрелка начнет валиться влево, и никаких показаний не будет. Для цифровых же приборов ошибка не станет большой проблемой – просто перед числовым показателем на дисплее появится минус. Тем не менее, «культура пользования» все же предполагает правильное расположение полярности. Тем более что бывают ситуации, когда это имеет важное значение. И хорошо, если правильное расположение щупов просто войдет в привычку.
Вернемся к проверке. Измерение напряжения – это лишь первый шаг, позволяющий отсеять явно негодные элементы питания. А само значение еще ни о чем не говорит – неизвестно, как поведет себя батарейка под нагрузкой. Поэтому и следует проверить ее еще и по току.
Для этого мультиметр переключается в режим DCA с максимальным пределом измерения, то есть на 10 или 20 А (в зависимости от модели прибора). Это важно, так как токи при замыкании батарейки через амперметр бывают нешуточные. Красный провод, естественно, переставляется в соответствующее гнездо.
После этого опять черный провод прикладывается к отрицательному полюсу батарейки. А красным производят кратковременное замыкание цепи на положительном полюсе. Это очень важный момент: замер не должен превышать одной – двух секунд. Можно постараться уложиться и менее чем за секунду. Необходимо быстро засечь пиковое значение силы тока, когда оно перестанет расти. Если же затянуть с измерением, это повлечет активный разряд элемента питания.
Проверка силы тока при замыкании батарейки через мультиметр должна проводиться максимально быстро. На иллюстрации – показатель в 5 ампер говорит о том, что элемент питания в отличном состоянии.
- В новых, качественных элементах питания проверка может показать порядка 4÷6 ампер. Они подойдут для самых ответственных мест установки.
- Диапазон от 3 до 3.9 ампера говорят, что батарейка вполне работоспособная, хотя ее функциональные способности все же несколько снижены. Но она еще послужит немало.
- От 2 до 3 ампер – элемент питания уже «посажен», но еще вполне пригоден для использования в приборах с незначительным потреблением энергии.
- Менее 2 ампер – батарейка, скорее всего, пригодна лишь для пульта дистанционного управления.
- Ну а если ток едва достигает 1.1 ампер или ниже – это почти всё. Возможно, такую батарейку еще можно поставить в пульт ДУ, но только если на текущий момент вообще нет другой замены. И вполне можно ожидать, что отказ в работе способен произойти в любой момент.
Проведя такую ревизию нередко скапливающегося дома запаса батареек, можно сразу избавиться от «балласта». А остальные — отсортировать по возможности дальнейшего применения.
Проверка тока утечки электросети автомобиля
Еще одно практическое приложение измерения силы тока мультиметром. Это — самостоятельная диагностика своего автомобиля на предмет токов утечки, которые способны привести к быстрому разряду аккумулятора.
Проводится она примерно в следующем порядке:
- Проверка должна проводиться при полностью заряженном аккумуляторе.
- Перед тестированием требуется выключить все потребляющие электроэнергию приборы. Имеется в виду освещение, аудиосистема, парктроник, и т.п. При проверке, возможно, придётся открывать двери в салон. Поэтому необходимо каким-то образом закрепить в нажатом положении концевые выключатели, ответственные за габаритные огни на дверях.
Безусловно, следует учитывать и иные особенности своего авто. Так, нередко требуется определенное время на полное «засыпание» бортового компьютера. Могут быть нюансы и с системой сигнализации. Хозяин машины должен с этим разобраться.
- С клеммы аккумулятора снимается кабель массы («минус»).
- Мультитестер переводится в режим амперметра с пределом измерений постоянного тока до 10 ампер. Ток утечки, безусловно, намного меньше, но подстраховаться никогда не мешает. А на точности снятия показаний это особо не отразится – двух знаков после десятичной запятой будет вполне достаточно. Красный провод устанавливается в соответствующее гнездо на 10 А.
- Далее, черный провод мультитестера необходимо подсоединить к минусовой клемме аккумулятора. Это можно сделать, например, с использованием обычного хомута.
- Замыкаться же цепь будет контактом щупа красного провода с клеммной снятого кабеля массы. Значение, высвечивающееся при этом на дисплее мультиметра, как раз и покажет ток утечки.
Подключение мультиметра для определения тока утечки. В данном случае – он явно превышает допустимые пределы.
Нормальным считается ток утечки в пределах 0,03÷0,05 А (30 ÷ 50 мА), и чем ниже, тем лучше. Иногда может быть и больше, если автомобиль «нафарширован» электроникой. Но даже в таком случае – никак не выше 0,08 А.
- Если ток в пределах нормы – то можно только порадоваться. Но в том случае, когда он явно выходит за пределы допустимого, следует сразу локализовать проблему, то есть выявить участок, где такая утечка происходит.
- Для этого последовательно вынимаются предохранители, отвечающие за разные участки электросети автомобиля. При этом необходимо проверить все – не только в коробке под капотом, но и размещенные в салоне.
Итак, предохранитель достали из гнезда. Если показания не изменились, его можно сразу вернуть на место. Значит, на этом участке проблем нет.
- Рано или поздно снятие какого-то предохранителя приведет к резкому снижению показаний силы тока на мультиметре. Вот он – тот самый участок, более детальной диагностикой которого предстоит заняться.
Кстати, причин утечки может быть и несколько. Например, снятие одного из предохранителей снизило показания силы тока с 0,25 до 0,12 А. Да, это проблемный участок, но очевидно, что ток все равно великоват. Значит, не устанавливая обратно этот предохранитель, поиск продолжают, пока не будет отыскано следующее «слабое звено». И так далее – пока показатель утечки не войдет в пределы нормы.
Тестирование показывает – ток утечки вошел в допустимые пределы
Ну а дальше – предстоит проводить более детальную диагностику, чтобы окончательно разобраться с проблемой. Но это уже – совсем другая тема.
11,2 Закон Ома | Электрические цепи
11,2 Закон Ома (ESBQ6)
Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводе и может быть описана как
.
\ (I = \ frac {V} {R} \)
где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток — на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как
\ [\ frac {I} {V} = \ frac {1} {R}.\]
Это можно изменить с точки зрения постоянного сопротивления как:
\ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор в цепь и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Высокие оценки в науке — залог вашего успеха и будущих планов.Проверьте себя и узнайте больше о практике Сиявулы.
Зарегистрируйтесь и проверьте себя
Закон Ома
Учебник Упражнение 11.1
Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямой, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *}
m & = \ frac {\ Delta I} {\ Delta V} \\
& = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\
& = \ текст {0,13}
\ end {выровнять *}
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]
Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.
\ begin {align *}
V_ {0} & = IR_ {0} \\
I & = \ frac {V_ {0}} {R_ {0}} \\
V_ {U} & = IR_ {U} \\
I & = \ frac {V_ {U}} {R_ {U}} \\
\ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\
\ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}}
\ end {выровнять *}
Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток через них.Эти проводники называются омическими проводниками, проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерьте ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа цепей.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему цепи, прежде чем производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:
Уравнение закона Ома:
\ [R = \ frac {V} {I} \]
, который можно преобразовать в:
\ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\
& = \ текст {1} \ текст {А}
\ end {align *}
Рабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя:
\ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).
\ begin {align *}
R & = \ frac {V} {I} \\
R \ times I & = \ frac {V} {I} \ times I \\
V & = I \ раз R \\
& = \ текст {10} \ times \ text {4} \\
& = \ текст {40} \ текст {V}
\ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Высокие оценки в науке — залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.
Зарегистрируйтесь и проверьте себя
Закон Ома
Учебник Упражнение 11.2
Вычислите сопротивление резистора, разность потенциалов которого равна \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
.
\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {8} {2} \\
& = \ текст {4} \ текст {Ω}
\ end {выровнять *}
Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
.
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {18} {6} \\
& = \ текст {3} \ текст {А}
\ end {выровнять *}
Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
.
\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {1,5}) (10) \\
& = \ текст {15} \ текст {V}
\ end {выровнять *}
Переплет резисторов последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
.
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\
& = \ текст {18} \ текст {Ω}
\ end {align *}
Эквивалентное параллельное сопротивление
В цепи, в которой резисторы соединены параллельно, эквивалентное сопротивление определяется следующим определением.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *}
\ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \верно) \\
& = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\
& = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\
& = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\
R_ {p} & = \ text {0,625} \ text {Ω}
\ end {align *}
Последовательное и параллельное сопротивление
Учебное пособие Упражнение 11.3
Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]
Эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
& = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\
& = \ текст {20} \ текст {кОм}
\ end {выровнять *}
Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]
Эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
R_ {2} & = R_ {s} — R_ {1} \\
& = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\
& = \ текст {90} \ текст {Ω}
\ end {выровнять *}
Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]
Эквивалентное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\
& = \ frac {1 + 10} {\ text {100}} \\
& = \ frac {11} {\ text {100}} \\
R_ {p} & = \ text {9,09} \ text {kΩ}
\ end {выровнять *}
Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]
Эквивалентное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\
& = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\
& = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\
& = \ frac {\ text {6,25}} {\ text {37,5}} \\
R_ {2} & = \ текст {6} \ текст {Ω}
\ end {выровнять *}
Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]
Эквивалентное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\
& = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\
& = \ frac {\ text {5}} {\ text {6}} \\
R & = \ текст {1,2} \ текст {Ω}
\ end {выровнять *}
b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]
Эквивалентное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\
& = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\
& = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\
& = \ frac {\ text {25}} {\ text {12}} \\
R & = \ text {0,48} \ text {Ω}
\ end {выровнять *}
c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]
Эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
& = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\
& = \ текст {5} \ текст {Ω}
\ end {выровнять *}
d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]
Эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\
& = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\
& = \ текст {10} \ текст {Ω}
\ end {выровнять *}
Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.
Последовательные цепи
Рассмотрим схему, состоящую из трех резисторов и
одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]
Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]
Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов, включенных последовательно, мы можем решить некоторые проблемы схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора омические по своей природе.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]
Следовательно,
\ begin {align *}
R & = \ текст {2} + \ текст {4} \\
& = \ текст {6} \ текст {Ω}
\ end {align *}
Применить закон Ома
\ begin {align *}
R & = \ frac {V} {I} \\
R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\
I & = \ frac {V} {R} \\
& = \ frac {12} {6} \\
& = \ текст {2} \ текст {А}
\ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:
\ [R = R_ {1} + R_ {2} \]
, потому что он находится в последовательной цепи.
Найдите полное сопротивление
\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {\ text {1,5}} {\ text {0,25}} \\
& = \ текст {6} \ текст {Ω}
\ end {align *}
Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]
и что
\ [R_ {1} = \ text {1} \ text {Ω} \]
с
\ [R = R_ {1} + R_ {2} \]
\ [R_ {2} = R — R_ {1} \]
Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]
Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I} \\
I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\
V_1 & = {I} \ cdot {R_1} \\
& = 2 \ cdot 1 \\
V_1 & = \ текст {2} \ текст {V}
\ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома:
\ begin {align *}
R_2 & = \ frac {V_2} {I} \\
I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\
V_2 & = {I} \ cdot {R_2} \\
& = 2 \ cdot 3 \\
V_2 & = \ текст {6} \ текст {V}
\ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Поскольку падение напряжения на всех резисторах вместе должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя:
\ begin {align *}
V & = V_1 + V_2 + V_3 \\
V_3 & = V — V_1 — V_2 \\
& = 18-2-6 \\
V_3 & = \ текст {10} \ текст {V}
\ end {align *}
Найдите сопротивление \ (R_3 \)
Мы знаем напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления:
\ begin {align *}
R_3 & = \ frac {V_3} {I} \\
& = \ frac {10} {2} \\
R_3 & = \ text {5} \ Omega
\ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
Параллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что
напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}. \]
Второй принцип параллельной схемы заключается в том, что все токи, проходящие через каждый резистор, должны составлять общий ток в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}.\]
Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы можем теперь подойти к некоторым проблемам схемы, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная схема
Вычислите ток (I) в этой цепи, если оба резистора омические по своей природе.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите эквивалентное сопротивление в цепи
.
Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \]
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\
& = \ frac {1} {2} + \ frac {1} {4} \\
& = \ frac {2 + 1} {4} \\
& = \ frac {3} {4} \\
\ text {Следовательно,} R & = \ text {1,33} \ Omega
\ end {align *}
Применить закон Ома
\ begin {align *}
R & = \ frac {V} {I} \\
R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\
I & = \ frac {V} {R} \\
I & = V \ cdot \ frac {1} {R} \\
& = (12) \ left (\ frac {3} {4} \ right) \\
& = \ текст {9} \ текст {А}
\ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная схема
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Поскольку резисторы омические и нам даны напряжение на элементе и ток через элемент, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {9} {\ text {4,8}} \\
& = \ text {1,875} \ \ Omega
\ end {align *}
Рассчитайте значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \).
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2}
\ end {выровнять *}
Переставляем решение для \ (R_2 \):
\ begin {align *}
\ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\
& = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\
& = \ текст {0,2} \\
R_2 & = \ frac {1} {\ text {0,2}} \\
& = \ текст {5} \ \ Omega
\ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
Рабочий пример 7: Закон Ома, параллельная схема
Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому:
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\
& = \ frac {1} {4} + \ frac {1} {12} \\
& = \ frac {3 + 1} {12} \\
& = \ frac {4} {12} \\
R & = \ frac {12} {4} = \ text {3} \ \ Omega
\ end {выровнять *}
Теперь, используя закон Ома, чтобы найти ток через ячейку:
\ begin {align *}
R & = \ frac {V} {I} \\
I & = \ frac {V} {R} \\
& = \ frac {18} {3} \\
I & = \ text {6} \ text {A}
\ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы:
\ begin {align *}
V & = V_1 = V_2 = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с расчета тока через \ (R_1 \) по закону Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I_1} \\
I_1 & = \ frac {V_1} {R_1} \\
& = \ frac {18} {4} \\
I_1 & = \ text {4,5} \ text {A}
\ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \):
\ begin {align *}
R_2 & = \ frac {V_2} {I_2} \\
I_2 & = \ frac {V_2} {R_2} \\
& = \ frac {18} {12} \\
I_2 & = \ text {1,5} \ text {A}
\ end {выровнять *}
Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через ячейку:
\ begin {align *}
I & = I_1 + I_2 \\
I_2 & = I — I_1 \\
& = 6 — 4.5 \\
I_2 & = \ text {1,5} \ text {A}
\ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Учебное упражнение 11.4
Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:
\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {9} {1} \\
& = \ текст {9} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем найти неизвестное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\
R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\
& = 9 — 3 — 3 — 1 \\
& = \ текст {2} \ текст {Ω}
\ end {выровнять *}
Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ text {1} + \ text {2,5} + \ text {1,5} \\
& = \ текст {5} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем рассчитать текущую:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {9} {5} \\
& = \ текст {1,8} \ текст {А}
\ end {выровнять *}
Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.
Рисуем принципиальную схему:
Теперь мы находим общее сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ текст {1} + \ текст {5} + \ текст {10} \\
& = \ текст {16} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем рассчитать текущую:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {12} {16} \\
& = \ текст {0,75} \ текст {A}
\ end {выровнять *}
Рассчитайте ток через ячейку, если оба резистора омические по своей природе.
Сначала находим общее сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\
& = \ frac {3 + 1} {\ text {3}} \\
& = \ frac {4} {\ text {3}} \\
& = \ текст {0,75} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем рассчитать текущую:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {9} {\ text {0,75}} \\
& = \ текст {12} \ текст {А}
\ end {выровнять *}
Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {24} {\ text {2}} \\
& = \ текст {12} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\
\ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ гидроразрыв {1} {R_ {3}} \\
& = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text { 60}} \\
& = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\
& = \ frac {4} {\ text {120}} \\
& = \ текст {30} \ текст {Ω}
\ end {выровнять *}
значение тока через аккумулятор
Рисуем принципиальную схему:
Чтобы вычислить значение тока через батарею, нам сначала нужно вычислить эквивалентное сопротивление:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\
& = \ frac {10 + 2 + 1} {\ text {10}} \\
& = \ frac {13} {\ text {10}} \\
& = \ текст {0,77} \ текст {Ω}
\ end {выровнять *}
Теперь можем посчитать ток через батарею:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {0,77}} \\
& = \ текст {26} \ текст {А}
\ end {выровнять *}
значение тока в каждом из трех резисторов.
Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]
Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {1}} \\
& = \ текст {20} \ текст {А}
\ end {выровнять *}
Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {5}} \\
& = \ текст {4} \ текст {А}
\ end {выровнять *}
И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {10}} \\
& = \ текст {2} \ текст {А}
\ end {выровнять *}
Вы можете проверить, что они в сумме составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, которые объединяют эти две схемы, например, следующую схему:
Рисунок 11.1:
Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.
Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.
Начнем с расчета общего сопротивления параллельной цепи 1 .{-1} \\
& = \ текст {5} \, \ Omega
\ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление:
\ begin {align *}
R & = R_ {p1} + R_ {p2} \\
& = 5 + 5 \\
& = 10 \, \ Omega
\ end {align *}
Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).
Последовательные и параллельные сети
Учебное пособие, упражнение 11.5
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {4} + \ frac {1} {2} \\
& = \ frac {3} {4} \\
R_ {p} & = \ text {1,33} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {3} + R_ {p} \\
& = \ текст {2} + \ текст {1,33} \\
& = \ текст {3,33} \ текст {Ω}
\ end {выровнять *}
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {1} + \ frac {1} {2} \\
& = \ frac {3} {2} \\
R_ {p} & = \ text {0,67} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\
& = \ текст {4} + \ текст {6} + \ текст {0,67} \\
& = \ текст {10,67} \ текст {Ω}
\ end {выровнять *}
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\
& = \ frac {23} {15} \\
R_ {p} & = \ text {0,652} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {4} + R_ {p} \\
& = \ текст {2} + \ текст {0,652} \\
& = \ текст {2,652} \ текст {Ω}
\ end {выровнять *}
ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\
& = \ frac {23} {15} \\
R_ {p} & = \ text {0,652} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {4} + R_ {p} \\
& = \ текст {2} + \ текст {0,652} \\
& = \ текст {2,652} \ текст {Ω}
\ end {выровнять *}
Итак, ток через ячейку:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {12}} {\ text {2,652}} \\
& = \ текст {4,52} \ текст {А}
\ end {выровнять *}
ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):
\ begin {align *}
V & = I \ cdot R \\
& = (\ text {4,52}) (\ text {0,652}) \\
& = \ текст {2,95} \ текст {V}
\ end {выровнять *}
Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {2,95}} {\ text {5}} \\
& = \ текст {0,59} \ текст {A}
\ end {выровнять *}
Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {2} + \ frac {1} {4} \\
& = \ frac {3} {4} \\
R_ {p} & = \ text {1,33} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {p} \\
& = \ text {4,66} + \ text {1,33} \\
& = \ текст {5,99} \ текст {Ω}
\ end {выровнять *}
Итак, напряжение на ячейке:
\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {5,99}) \\
& = \ текст {12} \ текст {V}
\ end {выровнять *}
Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с нахождения напряжения на \ (R_ {1} \):
\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {4,66}) \\
& = \ текст {9,32} \ текст {V}
\ end {выровнять *}
Теперь находим напряжение на параллельной комбинации:
\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {1,33}) \\
& = \ текст {2,66} \ текст {V}
\ end {выровнять *}
Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).
ток через ячейку
Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {1} + \ frac {1} {1} \\
& = 2 \\
R_ {p} & = \ text {0,5} \ text {Ω}
\ end {выровнять *}
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *}
R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\
& = \ text {2} + \ text {1,5} + \ text {0,5} \\
& = \ текст {4} \ текст {Ω}
\ end {выровнять *}
Итак, ток через ячейку:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {10}} {\ text {4}} \\
& = \ текст {2,5} \ текст {А}
\ end {выровнять *}
падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *}
V & = I \ cdot R \\
& = (\ text {2,5}) (\ text {1,5}) \\
& = \ текст {3,75} \ текст {V}
\ end {выровнять *}
ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *}
V & = I \ cdot R \\
& = (\ text {2,5}) (\ text {0,5}) \\
& = \ текст {1,25} \ текст {V}
\ end {выровнять *}
Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на всех резисторах в параллельной комбинации:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {1,25}} {\ text {1}} \\
& = \ текст {1,25} \ текст {А}
\ end {выровнять *}
параллельных цепей
Ваш браузер не поддерживает Java-апплеты
Схема с более чем одним
Путь прохождения тока представляет собой параллельную цепь.
НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Общее напряжение равно
напряжение любого параллельного сопротивления.
ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Полный ток равен
сумма тока каждого параллельного компонента.
ПАРАЛЛЕЛЬНОЕ СОПРОТИВЛЕНИЕ
ЦЕПИ
Общее сопротивление может быть
рассчитывается по закону Ома, если известны напряжение и полный ток.
Общее сопротивление всегда
меньше наименьшего значения сопротивления.
Метод равных значений
Для параллельных сопротивлений в
какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле
разделив номинал одного из резисторов на количество резисторов.
Взаимный метод
Для параллельных сопротивлений в
какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле
разделив номинал одного из резисторов на количество резисторов.
1 / R T = 1 / R 1 + 1 / R 2 + 1 / R N
R EQ = 1 / (1 / R 1 + 1 / R 2 +
… + 1 / R N
)
Метод произведения на сумму
Для расчета сопротивления
двух резисторов параллельно можно использовать эту формулу:
R EQ = (R 1 * R 2 ) / (R 1 + R 2 )
Правило приближения 10 к 1
Если подключены два резистора
параллельно, и один резистор в 10 или более раз больше, чем другой
резистор, резистор большего номинала можно не учитывать.
ПРОВОДИМОСТЬ
Общая проводимость равна
сумме проводимости каждого компонента.
ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Суммарная мощность равна
сумма мощности каждого компонента. (Это то же самое, что и с серией
схемы).
Правила для параллельных цепей постоянного тока
- Такое же напряжение существует
через каждую ветвь параллельной цепи и равно напряжению источника. - Ток через
параллельная ветвь обратно пропорциональна величине сопротивления
ветвь. - Полный ток
параллельная цепь равна сумме отдельных токов ответвления
цепь - Эквивалентное сопротивление
параллельная цепь находится по общему уравнению Req = 1 / (1 / R1 + 1 / R2 +
1 / номер) - Общая мощность, потребляемая в
параллельная схема равна сумме мощности, потребляемой индивидуумом
резисторы.
ПАРАЛЛЕЛЬНЫЙ АНАЛИЗ ЦЕПЕЙ
- Соблюдайте принципиальную схему
внимательно или при необходимости нарисуйте. - Обратите внимание на указанные значения и
значения, которые необходимо найти. - Выберите подходящий
уравнения, которые будут использоваться при решении для неизвестных величин на основе известных
количества. - Подставьте известные значения
в уравнении, которое вы выбрали, и решите для неизвестного значения.
ПАРАЛЛЕЛЬНОЕ УСТРАНЕНИЕ НЕПОЛАДОК
ЦЕПИ
Когда в
ветви параллельной сети сопротивление ветви увеличивается и
общее сопротивление цепи увеличивается. Это вызывает уменьшение общего
Текущий.
Короткое замыкание всегда приводит
в отсутствие тока, протекающего через другие ветви цепи.
Мощность и энергия
- Изучив этот раздел, вы сможете:
- Выполнять расчеты мощности, напряжения, тока и сопротивления.
- • с использованием соответствующих единиц и подразделов.
- Различение мощности и энергии в электрических цепях.
Мощность резисторов
Когда через резистор протекает ток, электрическая энергия преобразуется в ТЕПЛОВУЮ энергию. Тепло, генерируемое в компонентах цепи, каждый из которых обладает хотя бы некоторым сопротивлением, рассеивается в воздухе вокруг компонентов. Скорость рассеивания тепла называется МОЩНОСТЬЮ, обозначается буквой P и измеряется в ваттах (Вт).
Количество рассеиваемой мощности может быть вычислено с использованием любых двух величин, используемых в расчетах по закону Ома. Помните, как и в любой формуле, в формуле должны использоваться ОСНОВНЫЕ КОЛИЧЕСТВА, то есть ВОЛЬТЫ, ОМЫ и АМПЕРЫ (не милли, мег и т. Д.).
Чтобы найти мощность P, используя V и I
Чтобы найти мощность P, используя V и R
Чтобы найти мощность P, используя I и R
Перед тем, как начать, подумайте об этих нескольких советах, они облегчат решение, если внимательно следовать им.
1. Разработайте ответы с помощью карандаша и бумаги; в противном случае легко запутаться на полпути и получить неправильный ответ.
2. Конечно, ответ — это не просто число, это будет определенное количество ватт (или несколько или несколько единиц ватт). Не забудьте указать правильную единицу измерения (например, Вт или мВт и т. Д.), А также число, иначе ответ не имеет смысла.
3. Преобразуйте все вспомогательные единицы, такие как мВ или кОм, в ватты, указав их в соответствующей формуле.Ошибка здесь даст действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
4. Хотя структура этих формул мощности кажется очень похожей на формулы закона Ома, есть небольшое различие — они содержат некоторые элементы в квадрате (I 2 и V 2 ). Будьте очень осторожны при использовании трюка с треугольником для транспонирования этих формул. Если вам нужно связать мощность с сопротивлением, то I или V необходимо возвести в квадрат (умножить на себя). Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Не забудьте загрузить нашу брошюру «Подсказки по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы иметь дело с этими частями и каждый раз получать правильный ответ.
Нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети.Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.
Важно помнить о влиянии рассеивания мощности в компонентах: чем больше мощность, тем больше тепла должно рассеиваться компонентом. Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением.Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный отказ компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB). В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с помощью более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут даже быть заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла.Примеры резисторов большой мощности показаны на странице конструкции резистора.
Такие компоненты, как резисторы, имеют определенную номинальную мощность, указанную производителем (в ваттах или милливаттах). Этот рейтинг (параметр) необходимо проверять при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
НАКОНЕЧНИК
Тепло, выделяемое резисторами большой мощности, является основной причиной преждевременного выхода из строя многих цепей.Либо сам резистор выходит из строя из-за «разомкнутой цепи», особенно в резисторах с проволочной обмоткой. В резисторах из углеродного состава длительный перегрев может привести к изменению значения. Это может увеличиваться в типах с высоким сопротивлением или более опасно уменьшаться (позволяя увеличить ток) в типах с низким сопротивлением. Увеличение протекания тока, вызванное этим уменьшением сопротивления, только ускоряет процесс, и в конечном итоге резистор (а иногда и другие связанные компоненты) сгорает!
Энергия в резисторах
Если определенное количество мощности рассеивается в течение заданного времени, то рассеивается ЭНЕРГИЯ.Энергия (мощность x время) измеряется в Джоулях, и, включив время (t) в формулы мощности, можно рассчитать энергию, рассеиваемую компонентом или схемой.
Рассеиваемая энергия = Pt или VIt или V 2 t / R или даже I 2 Rt Джоуль
Обратите внимание, что в формулах для энергии такие величины, как мощность, время, сопротивление, ток и напряжение, должны быть преобразованы в их основные единицы, например Ватты, секунды, Ом, Амперы, Вольт и т. Д.Никаких дополнительных единиц или нескольких единиц! Как описано в буклете «Советы по математике».
Все вышеперечисленные единицы являются частью интегрированной системы международно стандартизированных единиц; Система S.I. (Système International d´Unités). Эта система устанавливает основные единицы для любых электрических, механических и физических свойств и их отношения друг к другу. Он также включает в себя стандартную форму кратных и подкратных чисел, описанную в буклете «Подсказки по математике».
Согласно закону Ома, I ∝ V, но I 1 / V в уравнении мощности.Как?
In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?
Это еще один запутанный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.
Согласно закону Ома, ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI). Как объяснить?
т.е.
- По закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
- Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)
Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V, он показывает Этот ток обратно пропорционален напряжению.
Давайте проясним путаницу, связанную с утверждением.
P = V x I
Фактически, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной или она меняется.
- Если мощность источника постоянна, ток будет уменьшаться при увеличении напряжения.
- Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при увеличении напряжения, поскольку мощность больше не постоянна i.е. мощность также была увеличена.
В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).
В = I x R
По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.
Согласно формуле мощности, в ней говорится, что ток обратно пропорционален напряжению, если мощность остается прежней.
Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение мощность). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.
Та же история и с генерирующей станцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.
Вкратце:
- Если мощность постоянна = Напряжение обратно пропорционально току , т.е. В ∝ 1 / I в P = VxI .
- Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , т. Е. В I в В = IxR .
Это точная причина , почему по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.
Связанные вопросы / ответы:
Руководство по номинальным характеристикам трансформатора, кВА
Перейти к:
Во многих отраслях промышленности, включая здравоохранение, производство, заключение контрактов на электроэнергию, высшее образование и исправительные учреждения, надежные высококачественные трансформаторы необходимы для обеспечения эффективной работы. Крупные предприятия и промышленные процессы требуют значительного количества энергии, и им нужны надежные трансформаторы для преобразования энергии, поступающей от электростанции, в форму, которую они могут использовать для своего оборудования и инженерных сетей.
Как трансформаторы помогают коммерческим и промышленным предприятиям достичь этих целей?
Трансформаторы преобразуют энергию источника в мощность, необходимую для нагрузки. Чтобы использовать свои трансформаторы эффективно, предприятиям необходимо знать, какую мощность могут дать им их трансформаторы. Эту информацию предоставляет рейтинг трансформатора.
Трансформатор обычно состоит из двух обмоток, первичной и вторичной обмоток. Входная мощность проходит через первичную обмотку.Затем вторичная обмотка преобразует мощность и отправляет ее на нагрузку через свои входные провода. Номинал трансформатора или его размер — это уровень его мощности в киловольт-амперах.
Когда какое-либо электрическое оборудование выходит из строя, часто виноват трансформатор. В этом случае вам, вероятно, потребуется заменить трансформатор, а когда вы это сделаете, вам нужно будет выбрать трансформатор с правильной кВА для ваших нужд. В противном случае вы рискуете поджарить свое ценное снаряжение.
Как выбрать размер трансформатора? К счастью, подобрать трансформатор относительно просто.Он включает в себя использование простой формулы для расчета требований кВА на основе тока и напряжения вашей электрической нагрузки. В приведенном ниже руководстве по номинальной мощности трансформатора кВА мы более подробно объясним, как рассчитать требуемую номинальную мощность в кВА.
Для получения дополнительной информации позвоните в ELSCO
Как определить мощность в кВА
Когда вы рассчитываете мощность в кВА, полезно иметь терминологию и сокращения прямо перед тем, как вы начнете. Иногда можно встретить трансформаторы, особенно меньшего размера, с размерами в ВА.ВА расшифровывается как вольт-амперы. Например, трансформатор с номинальной мощностью 100 ВА может выдерживать напряжение 100 В при токе в один ампер (ампер).
Единица измерения кВА представляет собой киловольт-ампер или 1000 вольт-ампер. Трансформатор с номинальной мощностью 1,0 кВА аналогичен трансформатору с номинальной мощностью 1000 ВА и может выдерживать напряжение 100 В при токе 10 ампер.
Расчет кВА Типоразмер
Чтобы определить мощность в кВА, вам необходимо выполнить ряд расчетов на основе вашей электрической схемы.
Электрическая нагрузка, которая подключается к вторичной обмотке, требует определенного входного напряжения или напряжения нагрузки. Назовем это напряжение V. Вам нужно знать, что это за напряжение — вы можете найти его, посмотрев на электрическую схему. Можно сказать, что в примере напряжение нагрузки V должно составлять 150 вольт.
Затем вам нужно будет определить конкретный ток, необходимый для вашей электрической нагрузки. Вы также можете посмотреть на электрическую схему, чтобы определить это число. Если вы не можете определить требуемый ток, его можно рассчитать, разделив входное напряжение на входное сопротивление.Допустим, требуемый ток фазы нагрузки, который мы назовем l, составляет 50 ампер.
После того, как вы нашли или рассчитали эти две цифры, вы можете использовать их, чтобы вычислить потребляемую нагрузкой мощность в киловаттах. Для этого вам нужно умножить требуемое входное напряжение (В) на требуемую токовую нагрузку в амперах (л), а затем разделить это число на 1000:
.
В приведенном выше примере вы должны умножить 150 на 50, чтобы получить 7 500, а затем разделить это число на 1000, чтобы получить 7,5 киловатт.
Последний шаг — преобразовать цифру в киловаттах в киловольт-амперы. Когда вы это сделаете, вам нужно будет разделить на 0,8, что представляет собой типичный коэффициент мощности нагрузки. В приведенном выше примере вы разделите 7,5 на 0,8, чтобы получить 9,375 кВА.
Однако, выбирая трансформатор, вы не найдете трансформатора мощностью 9,375 кВА. Большинство номинальных значений кВА являются целыми числами, а многие, особенно в более высоких диапазонах, кратны пяти или 10–15 кВА, 150 кВА, 1000 кВА и так далее. В большинстве случаев вам нужно выбрать трансформатор с номинальной мощностью немного выше рассчитанной вами кВА — в данном случае, вероятно, 10 или 15 кВА.
Вы также можете работать в обратном направлении и использовать известную мощность трансформатора в кВА для расчета силы тока, которую вы можете использовать. Если ваш трансформатор рассчитан на 1,5 кВА, и вы хотите, чтобы он работал при 25 вольт, умножьте 1,5 на 1000, чтобы получить 1500, а затем разделите 1500 на 25, чтобы получить 60. Ваш трансформатор позволит вам работать с током до 60 ампер. Текущий.
Если идея выполнения расчетов, когда вам нужно вычислить кВА, кажется устрашающей или непривлекательной, вы всегда можете обратиться к диаграммам. Многие производители предоставляют диаграммы, чтобы упростить определение правильной мощности в кВА.Если вы используете диаграмму, вы найдете напряжение и силу тока вашей системы в строках и столбцах, а затем найдете в списке кВА, где пересекаются выбранные вами строка и столбец.
Запрос цены на трансформатор
Стартовый фактор и особенности специализации
В приведенном выше примере мы разделили на 0,8, чтобы немного увеличить кВА трансформатора. Почему мы это сделали?
Для запуска устройства обычно требуется больше тока, чем для запуска. Чтобы учесть это дополнительное текущее требование, часто бывает полезно включить начальный фактор в свои расчеты.Хорошее практическое правило — умножить напряжение на силу тока, а затем умножить на дополнительный пусковой коэффициент 125%. Деление на 0,8, конечно, то же самое, что умножение на 1,25.
Однако, если вы часто запускаете трансформатор — скажем, чаще, чем один раз в час — вам может потребоваться кВА даже больше, чем рассчитанный вами размер. А если вы работаете со специализированными нагрузками, например, с двигателями или медицинским оборудованием, ваши требования кВА могут существенно отличаться. Для специализированных приложений вам, вероятно, захочется проконсультироваться с профессиональной компанией по производству трансформаторов, чтобы узнать, какая кВА вам нужна.
Уравнение для трехфазных трансформаторов, которое мы обсудим более подробно ниже, также немного отличается. Когда вы выполняете расчеты с трехфазными трансформаторами, вам нужно включить константу, чтобы убедиться, что ваша работа работает правильно.
Стандартные размеры трансформатора
Легко говорить о расчетах размеров трансформатора абстрактно и придумать массив чисел. Но каковы стандартные размеры трансформаторов, которые вы могли бы купить?
Для коммерческих зданий наиболее распространенными размерами трансформаторов являются следующие:
- 3 кВА
- 6 кВА
- 9 кВА
- 15 кВА
- 30 кВА
- 37.5 кВА
- 45 кВА
- 75 кВА
- 112,5 кВА
- 150 кВА
- 225 кВА
- 300 кВА
- 500 кВА
- 750 кВА
- 1000 кВА
Как определить напряжение нагрузки
Прежде чем вы сможете рассчитать необходимую кВА для вашего трансформатора, вам нужно вычислить напряжение нагрузки, которое является напряжением, необходимым для работы электрической нагрузки. Чтобы определить напряжение нагрузки, вы можете взглянуть на свою электрическую схему.
В качестве альтернативы, у вас может быть кВА вашего трансформатора и вы хотите рассчитать необходимое напряжение. В этом случае вы можете скорректировать уравнение, которое мы использовали выше. Поскольку вы знаете, что кВА = V * 1/1000, мы можем решить для V, чтобы получить V = kVA * 1000 / л.
Итак, вы умножите свою номинальную мощность в кВА на 1000, а затем разделите на силу тока. Если ваш трансформатор имеет номинальную мощность 75 кВА, а ваша сила тока 312,5, вы подставите эти числа в уравнение — 75 * 1000 / 312,5 = 240 вольт.
Как определить вторичное напряжение
Первичная и вторичная цепи наматываются вокруг магнитной части трансформатора.Пара различных факторов определяет вторичное напряжение — количество витков в катушках, а также напряжение и ток первичной цепи.
Вы можете рассчитать напряжение вторичной цепи, используя соотношение падений напряжения в первичной и вторичной цепях, а также количество витков цепи вокруг магнитной части трансформатора. Мы будем использовать уравнение t 1 / t 2 = V 1 / V 2 , где t 1 — количество витков в катушке первичной цепи, t 2 — количество витков витков в катушке вторичной цепи, V 1 — это падение напряжения в катушке первичной цепи, а V 2 — это падение напряжения в катушке вторичной цепи.
Допустим, у вас есть трансформатор с 300 витками первичной обмотки и 150 витками вторичной обмотки. Вы также знаете, что падение напряжения на первой катушке составляет 10 вольт. Подставляя эти числа в приведенное выше уравнение, получаем 300/150 = 10 / t 2 , так что вы знаете, что t 2 , падение напряжения на вторичной катушке, составляет 5 вольт.
Как определить первичное напряжение
Помните, что у каждого трансформатора есть первичная и вторичная стороны. Во многих случаях вам нужно рассчитать первичное напряжение, то есть напряжение, которое трансформатор получает от источника питания.
Вы можете определить это первичное напряжение, используя соотношение тока и напряжения на первичной и вторичной обмотках трансформатора. Возможно, вы знаете, что ваш трансформатор имеет ток 4 ампера и падение напряжения на вторичной обмотке 10 вольт. Вы также знаете, что ваш трансформатор пропускает через первичную обмотку ток 6 ампер. Каким должно быть падение напряжения на первичной обмотке?
Пусть i 1 и i 2 равны токам через две катушки. Вы можете использовать формулу i 1 / i 2 = V 2 / V 1 .В этом случае i 1 равно 6, i 2 равно 4, а V 2 равно 10, и если вы подставите эти числа в формулу, вы получите 6/4 = 10 / V 1 . Решение для V 1 дает V 1 = 10 * 4/6, поэтому падение напряжения в первичной цепи должно составлять 6,667 вольт.
Запрос цены на трансформатор
Однофазный номинальный ток, кВА
Однофазный трансформатор использует однофазный переменный ток. Он имеет две линии переменного тока (AC).Ниже приведены несколько распространенных типов:
- залитый: Однофазный залитый трансформатор полезен для различных общих нагрузок, включая как внутренние, так и внешние нагрузки. Эти трансформаторы широко используются в промышленных и коммерческих операциях, включая многие типы осветительных приборов. При желании предприятия могут объединить эти блоки для создания трехфазных трансформаторов. Эти трансформаторы имеют относительно низкие номиналы, часто от 50 ВА до 25 кВА.
- Вентилируемый: Вентилируемый однофазный трансформатор используется для нескольких однофазных нагрузок внутри и вне помещений.Эти трансформаторы широко используются в коммерческих и промышленных приложениях, включая системы освещения. Они часто имеют номиналы от 25 до 100 кВА.
- Полностью закрытые невентилируемые трансформаторы : Полностью закрытые невентилируемые трансформаторы могут быть однофазными или трехфазными. Они идеально подходят для сред, содержащих большое количество грязи и мусора. Их номинальные характеристики обычно варьируются от 25 до 500 кВА.
Трехфазная мощность, кВА
Трехфазный трансформатор может иметь одну из нескольких различных форм.Обычно он имеет три линии питания, каждая из которых сдвинута по фазе с двумя другими на 120 градусов.
По сравнению с однофазными трансформаторами, трехфазные трансформаторы бывают аналогичных типов:
- залитый: Трехфазный залитый трансформатор полезен для множества общих нагрузок, как наружных, так и внутренних, коммерческих и промышленных, включая системы освещения. Эти трансформаторы часто имеют номинальные характеристики от 3 до 75 кВА.
- Вентилируемый: Трехфазный вентилируемый трансформатор полезен для многих типов общих внутренних и внешних нагрузок, как промышленных, так и коммерческих, включая системы освещения.Эти трансформаторы могут иметь огромные мощности, до 1000 кВА.
- Полностью закрытые, без вентиляции: как и однофазные блоки, эти трехфазные системы идеальны для сред, содержащих большое количество грязи и мусора. Их номинальные характеристики обычно варьируются от 25 до 500 кВА.
Расчет для трехфазного трансформатора кВА немного отличается от расчета для однофазного кВА. После того, как вы умножите свое напряжение и силу тока, вам также нужно будет умножить его на константу — 1.732, который представляет собой квадратный корень из 3, усеченный до трех десятичных знаков:
Итак, если вы работаете с трехфазным трансформатором, вместо того, чтобы умножать напряжение на силу тока и делить на 1000, чтобы получить кВА, вы умножаете напряжение на силу тока на 1,732 и все равно делите на 1000, чтобы получить кВА.
Обратитесь в ELSCO Transformers, чтобы получить помощь с трансформатором
Чтобы увидеть преимущества качественных, высокопроизводительных трансформаторов для вашего бизнеса, станьте партнером ELSCO Transformers.Мы предоставляем ряд услуг по обслуживанию трансформаторов, чтобы обеспечить бесперебойную работу вашего бизнеса, включая ремонт трансформаторов, реконструкцию, модернизацию, перемотку и аварийную замену.
Мы также предлагаем несколько различных типов новейших трансформаторов среднего напряжения, в том числе сухие трансформаторы, трансформаторы для установки на площадках, блочные подстанции и трансформаторы подстанционного типа. Мы также рады разработать трансформаторы, изготовленные по индивидуальному заказу, в соответствии с уникальными потребностями и спецификациями вашего предприятия. У нас есть многолетний опыт поставок трансформаторов для различных отраслей промышленности, включая подрядчиков по электротехнике, дома электроснабжения, больницы, медицинские клиники и производственные предприятия, а также многие другие.
Неисправный или неисправный трансформатор может привести к дорогостоящим задержкам и снизить прибыльность вашего бизнеса. Поддерживайте эффективную работу своей работы, следя за ремонтом трансформатора или приобретая новую систему от ELSCO Transformers. Наши основные сотрудники имеют более чем двадцатилетний опыт работы в отрасли, и мы используем этот обширный опыт, знания и опыт, чтобы предоставить вам надежные устройства, которые будут надежно работать и работать в течение многих лет.
Свяжитесь с нами сегодня, чтобы узнать больше.
Запрос цены на трансформатор
Ом, Ампер, Вольт и что вам нужно знать | Компоненты квеста
Ом, Ампер, Вольт и что вам нужно знать
При работе с электроникой чрезвычайно важно понимать основы электричества. Только в этом случае вы сможете правильно подобрать размер компонентов и убедиться, что ваши продукты безопасны. Вот что вам нужно знать о том, как измеряется электрический ток.
Измерение электроэнергии
Электричество состоит из четырех компонентов.Каждый состоит из разных единиц. Знание того, что представляет собой каждый компонент и как он измеряется, позволяет вам производить все необходимые вычисления для обеспечения безопасности и совместимости между электрическими частями.
- Напряжение (В) измеряется в вольтах (В).
- Ток (I) измеряется в амперах (A).
- Сопротивление (R) измеряется в омах (O).
- Мощность (P) измеряется в ваттах (Вт)
Вот основные правила, которые определяют, как эти измерения работают вместе:
Мощность = Напряжение * Ток или P = В * I
Следовательно, вы всегда можете рассчитать напряжение, ток или мощность, если знаете два из трех значений:
I = P / V и V = P / I
Закон
Ома объясняет взаимосвязь между напряжением, током и сопротивлением:
В = I * R
Другими словами, напряжение равно току, умноженному на сопротивление.Затем вы можете рассчитать напряжение, ток или сопротивление, если знаете значения двух из трех:
R = V / I или I = V / R
Определения
Имея в виду эти уравнения, давайте посмотрим, что на самом деле представляет собой каждый компонент.
Вольт: Если рассматривать электричество как эквивалент воды, протекающей по трубе, напряжение — это давление воды. Когда применяется «водяной насос» в виде батареи или источника питания, давление повышается, вызывая протекание «воды» или электрического тока.С увеличением напряжения увеличивается и сила тока.
Бытовые розетки в США имеют стандартное выходное напряжение 120 В. Одноэлементный аккумулятор имеет напряжение от 1,2 до 1,6 В, в то время как линии электропередач высокого напряжения выдают невероятные 110 000 вольт.
Ампер: Сокращенно от ампер, ампер измеряет электрический ток. В примере с водопроводной трубой ток — это скорость потока воды. Больший ток или больше ампер указывает на то, что протекает большее количество электричества.
Ом: Ом для измерения сопротивления в электрической системе. В водопроводной трубе труба добавляет сопротивление, контролируя количество и направление потока воды. В электрической цепи сопротивление эффективно сужает трубу, уменьшая ток.
Вт: Вт измеряют общую мощность системы или количество энергии, выделяемой в секунду. На него влияет как напряжение, так и сила тока.
Различные электронные компоненты играют разные роли в управлении напряжением, сопротивлением, током и общей мощностью системы.Чем больше вы знаете об этих отдельных частях уравнения, тем лучше вы сможете определить, что именно нужно вашему проекту.
Готовы начать работу?
Здесь, в Quest Components, мы стремимся предоставить вам информацию, необходимую для того, чтобы ваш бизнес продолжал работать бесперебойно. Компания, сертифицированная по стандарту ISO 9001: 2015, со штаб-квартирой в промышленности, Калифорния, Quest Components специализируется на пассивных и активных компонентах уровня платы. Мы также предоставляем различные услуги OEM-производителям (производителям оригинального оборудования) и CEM (контрактным производителям электроники) по всему миру.Свяжитесь с Quest Components сегодня по телефону 626-333-5858, чтобы получить все необходимые электронные компоненты!
Большой приклад. Быстрый ответ. Умные люди.
Напряжение — Энергетическое образование
Напряжение часто используется как сокращение для разности напряжений , что является другим названием для разности потенциалов . Напряжение измеряет энергию, которую получит заряд, если он перемещается между двумя точками в пространстве. Единицей измерения напряжения является вольт (В), а 1 вольт = 1 Дж / Кл. [2]
Розетки и батареи имеют связанные с ними напряжения. Фактически, когда электричество доставляется на любое расстояние, между начальной и конечной точками существует напряжение (также известное как разность потенциалов). Когда приложено напряжение, энергетически предпочтительно, чтобы электрический заряд двигался к точке самого низкого напряжения в проводе; это причудливый способ сказать, что положительный электрический заряд приобретает энергию при переходе от точки высокого напряжения к точке низкого напряжения.Отрицательный электрический заряд получит энергию от движения в другом направлении.
Чем больше напряжение, тем больше выигрыш в энергии от перемещения между двумя точками. Кроме того, чем больше заряд проходит через напряжение, тем больше кинетическая энергия, получаемая зарядом. Уравнение, которое моделирует это:
[математика] E = Q \ Delta V [/ математика]
Одна единственная точка не имеет напряжения, поскольку напряжение определяется как разность энергии между двумя точками.Напряжение всегда зависит от некоторой контрольной точки, которая определяется как 0 В. Для удобства Земля почти всегда определяется как 0 В (в классах физики 0 В часто рассматривается как потенциал в точке бесконечно удаленной, но это бесполезен в электронике). Напряжение генерирует поток электронов (электрический ток) через цепь. Специфическое название источника энергии, создающего напряжение для протекания тока, — электродвижущая сила. Это соотношение между напряжением и током задается законом Ома.
Часто бывает полезна аналогия:
Гравитационная потенциальная энергия — это энергия, которую мяч накапливает, сидя на столе. Высота, умноженная на ускорение свободного падения ( г ), дает полную энергию, которая преобразуется в кинетическую энергию, если мяч упадет с этой высоты. Электродвижущая сила — это то, что продолжает поднимать мяч и класть его обратно на стол (это то, что движет потоком мячей, падающих со стола).
Электрическая энергия — это энергия, выделяющаяся, когда заряд «падает» через разность потенциалов (напряжение).Напряжение существует независимо от того, есть заряд или нет.
Для бытового применения
Электрическая розетка в доме имеет напряжение 120 В (в Канаде и США) через два отверстия. Это напряжение присутствует всегда, и когда электрическая нагрузка становится частью цепи (например, путем подключения прибора), это напряжение заставляет ток течь по цепи.
Электрогенераторы перемещают магниты возле катушек с проводами для создания напряжения в электрической сети.
Генерация постоянного тока создает напряжения, используя энергию света в фотоэлектрических элементах или энергию химических реакций, обычно внутри батарей, и даже разницу температур с помощью термопар.Чтобы узнать больше о физике напряжения, см. Гиперфизику.
Аккумулятор 9В имеет напряжение 9В. Двойные батареи A, AAA, C и D имеют напряжение (разность потенциалов) 1,5 В.
Phet Simulation
Чем больше напряжение, тем больше тока проходит через цепь. Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета. Используя приведенное ниже моделирование, исследуйте, как увеличение напряжения увеличивает ток в цепи:
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
- ↑ Это изображение предоставлено кем-то из команды.
- ↑ R.T. Пэйнтер, «Основные электрические компоненты и счетчики», в Введение в электричество , 1-е изд. Нью-Джерси: Прентис-Холл, 2011, гл. 2, сек. 2.4, с. 49-50.
.



