2 \cdot h$
Площадь боковой поверхности:
$S = 2\cdot\pi\cdot r \cdot h$
Площадь полной поверхности:
$S = 2\cdot\pi\cdot r(h + r)$
Тест: объём и площадь поверхности
Как посчитать объем цилиндра — онлайн калькулятор
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3. 14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания S
o и высоту h
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
V = So⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см3
Зная площадь боковой поверхности S
b и высоту h
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
V = Sb2/4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3. 14⋅ 5 = 900/62.8 = 14.33 см3
14⋅ 5 = 900/62.8 = 14.33 см3
См. также
Как посчитать площадь коробки
Для чего нужно знать площадь заготовки картонной коробки?
Во-первых, от этого зависит размер листа гофрокартона, который нужен для вырубки коробки, а значит, и цена готового изделия.
Во-вторых, зная площадь и плотность материала, можно посчитать вес готовой гофротары, который нужно учесть при отправке груза любым транспортом. Конечно, точный вес короба может рассчитать только специалист, в особенности, если речь идет о гофроупаковке сложной высечки. Но для обычных четырехклапанных коробов этот расчет можно сделать самостоятельно с достаточной для практических целей точностью.
Что нужно знать
- Ширину (B), длину (A) и высоту (H) коробки в миллиметрах; Ширину клеевого клапана, для прочности коробки выберем ее равной 59 мм для 3-х слойного картона и 69 для 5-ти слойного; Длину нижних и верхних клапанов, для четырехклапанного короба она равна B/2; Толщину гофрокартона (припуск на сгиб при сборке).
Чаще всего коробки изготавливают из трехслойного или пятислойного гофрокартона.
Пошаговый расчет площади картонной коробки
где 59 – припуск на клеевой клапан и толщину гофрокартона, 8 – припуск на толщину гофрокартона.
где 69 – припуск на клеевой клапан и толщину гофрокартона,16 – припуск на толщину гофрокартона.
Т. к. размеры подставляем в миллиметрах, то для получения площади в квадратных метрах делим полученное число на 1000000.
Если вам нужны коробки сложной конфигурации по индивидуальным размерам, наша компания «МС-ПАК» изготовит их на заказ. Технологи рассчитают площадь гофрокартона, необходимого для производства и его стоимость, а также посчитают итоговую цену тиража.
Рассчитать площадь коробки онлайн
Для примера рассчитаем площадь четырехклапанного короба размеров 600*400*400 из трехслойного гофрокартона Т-23, который используют чаще всего. Размеры указаны в мм.
Пример расчета
После измерения получены значения: A=600 мм, B=400 мм, H=400 мм.
В результате получили S=1,7 м 2 .
Теперь, зная плотность картона, можно вычислить вес коробки как произведение площади заготовки на плотность материала. Средняя плотность трехслойного гофрокартона Р=350 г/м 2 , вес коробки равен 1,7*0,35=0,6 кг.
Чтобы правильно выбрать картонные коробки для конкретного груза, необходимо предварительно рассчитать ее объем. Эта величина максимально отображает вместимость гофротары.
Расчет объема коробок
Картонные коробки имеют квадратную или прямоугольную форму. В этом случае они представляют собой параллелепипед. Из школьного курса нам известно, что для расчета объема этой фигуры необходимы длина, ширина и высота . Размеры можно измерить с помощью обычной линейки или рулетки.
Расчет объема, исходя из размера коробки, можно произвести по формуле:
Формула для подсчета:
V=a*b*h .
Где a – длина основания (мм),
b – ширина основания (мм),
h – высота коробки (мм),
V – объем (л).
Эта формула представляет собой расчет объема параллелепипеда. Поэтому, ее можно использовать только для прямоугольных коробок.
Для тех случаев, когда тара имеет нестандартную форму, вычислить ее объем можно по формуле:
Формула для подсчета:
V=S*h .
Где S – площадь основания, которую рассчитывают в зависимости от его формы. В случае треугольного, шестиугольного или восьмиугольных оснований расчет площади выполняется по разным формулам.
Поскольку, единицей объема в международной системе измерений (СИ) являются кубические метры (м 3 ), то более правильно размер длины, ширины и высоты перевести в метры. Для тех, кто привык работать с сантиметрами или миллиметрами, можно оставить эту размерность. Но при расчете объема груза придется использовать только ее.
Внутренний и внешний объем коробки
Зная точный объем гофрокороба, можно без затруднений подобрать подходящий груз. Для этого по той же методике следует вычислить его объем. Если груз имеет сложную конфигурацию, то для расчетов нужно использовать габаритные размеры. Понятно, что объем тары должен быть немного больше.
Понятно, что объем тары должен быть немного больше.
При выборе груза нужно также учитывать, на основании внутренних или внешних размеров был рассчитан объем коробок. Результаты будут несколько отличаться. В некоторых случаях это может иметь значение.
По этой причине для точного определения допустимых размеров груза желательно использовать внутренние размеры тары. Габариты ящиков и грузов должны отличаться между собой на 5-10 мм. Наружные размеры коробок необходимы при заполнении кузова автотранспорта для их перевозки. Они могут также потребоваться при вычислении требующейся площади склада для хранения.
Пошаговая инструкция для вычисления объема
Мы ознакомились с необходимыми теоретическими сведениями по расчету объема коробки. Рассмотрим описанные выше действия пошагово.
Измеряем длину коробки. Под ней подразумевают размер самой длинной стороны основания. Используем для этого рулетку или линейку. Переводим полученный размер в метры и записываем. Для небольшой тары измерения проще проводить в сантиметрах или миллиметрах. Если вы решили использовать одну из этих размерностей, примите во внимание, что остальные размеры, в том числе и габариты груза, нужно измерять в той же размерности.
Для небольшой тары измерения проще проводить в сантиметрах или миллиметрах. Если вы решили использовать одну из этих размерностей, примите во внимание, что остальные размеры, в том числе и габариты груза, нужно измерять в той же размерности.
Измеряем ширину коробки. Это размер более короткой стороны основания. Применяем те же единицы измерения. Записываем или запоминаем полученный результат. Для полностью квадратных коробок длина и ширина совпадают.
Далее необходимо измерить высоту нашей тары. Под высотой понимают сторону, расположенную перпендикулярно основанию. Проще говоря, это расстояние от нижнего клапана коробки до верхнего.
На следующем этапе в соответствии с формулой вычисления объема все полученные размеры перемножаем. Если в процессе измерений мы выявили, что размер нашей коробки 100х200х300 мм , то объем в этом случае представляет собой произведение всех трех величин. V=100х200х300=6 000000 мм 3 или 0,006 м 3 .
В некоторых случаях существует необходимость перевести полученную величину в литры (л). Знание количества кубических единиц дает возможность понять, сколько таких кубов можно вместить внутри конкретной коробки. При расфасовке жидких, мелких или сыпучих товаров, которые занимают полный объем тары, необходимо это значение выразить в литрах. Для этого используем соотношение 1 м 3 = 1000 л. В нашем случае V = 0,006х1000=6 л .
Знание количества кубических единиц дает возможность понять, сколько таких кубов можно вместить внутри конкретной коробки. При расфасовке жидких, мелких или сыпучих товаров, которые занимают полный объем тары, необходимо это значение выразить в литрах. Для этого используем соотношение 1 м 3 = 1000 л. В нашем случае V = 0,006х1000=6 л .
Напоминаем, что эту методику можно применять только для картонных изделий прямоугольной или квадратной формы. Для других случаев придется вспомнить школьный курс геометрии более глубоко. Используйте формулу для нахождения площади многоугольника. По ней сможете вычислить площадь основания вашей тары. Умножив ее на высоту, легко получите величину объема.
Объем – это количественная характеристика пространства, занимаемого телом, конструкцией или веществом.
Формула расчета объема:
А – длина;
В – ширина;
С – высота.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.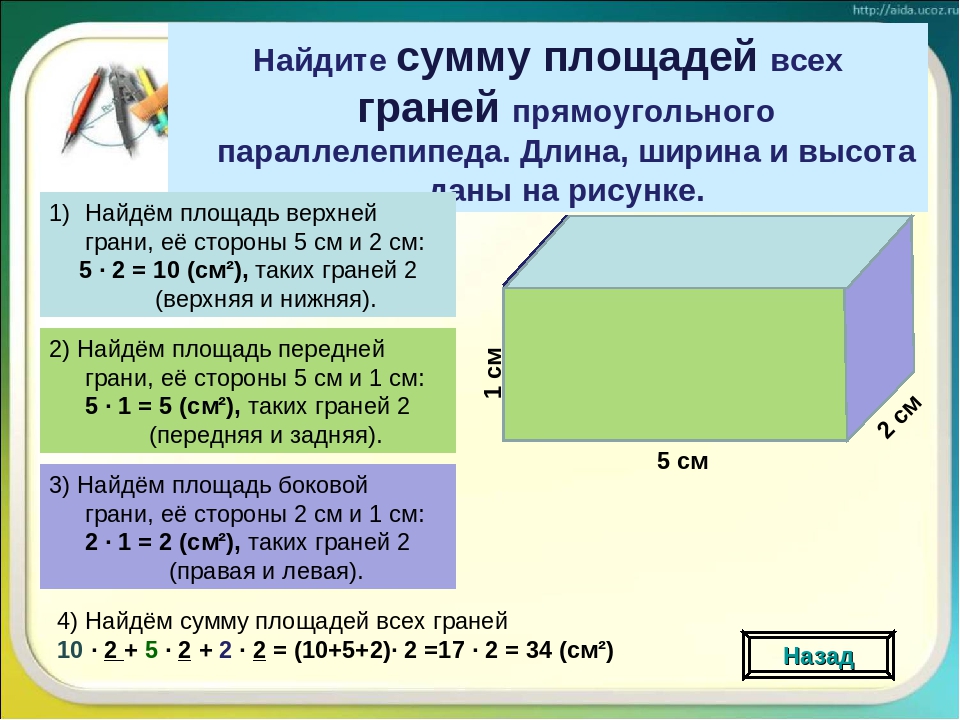
В нашей проектной организации Вы можете заказать расчет объема коробки на основании технологического или конструкторского задания.
На этой странице представлен самый простой онлайн калькулятор расчета объема коробки. С помощью этого калькулятора в один клик вы можете вычислить объем коробки, если известны длина, ширина и высота.
Как посчитать длину стен, зная площадь комнаты
Статья будет полезна тем, кто столкнулся с необходимостью рассчитать планировку комнат в новостройке. Имеющийся на руках план всегда содержит информацию о площадях помещений квартиры, но не всегда в нем есть информация о длинах стен, перегородок, дверных и оконных проемов и т.д. Мы расскажем о том, как восполнить этот недостаток, воспользовавшись незатейливыми математическими расчетами, которые будут понятны даже семикласснику.
Предположим, у нас есть план квартиры, такой как показан на рисунке ниже. Этот план нам потребуется в электронном виде – в виде картинки, которую мы сможем открыть графическим редактором (например, в формате . jpeg или .png).
jpeg или .png).
Если у Вас план только на бумаге, то можно его ровно без перекосов сфотографировать и сохранить в компьютер или загрузить с сайта застройщика, если такая возможность имеется.
В нем нам нужно выбрать любую комнату строго прямоугольной формы (или квадратной). В нашем примере выберем кухню, площадь которой нам известна, и составляет 15,13 квадратных метров.
Условно обозначим длину одной стороны прямоугольника буквой «a», длину другой «b», как принято в школьном курсе геометрии.
Площадь прямоугольника, как мы помним определяется произведением его сторон:
С помощью встроенного графического редактора Paint или другого, например, PickPick открываем наше изображение с планом квартиры. Затем с помощью инструмента «Выделение» вычисляем длину и ширину нашего прямоугольника в пикселях, как показано на рисунке ниже.
Полученные значения запишем, обозначив их, например, как «a» со штрихом и «b» со штрихом, для длины и ширины комнаты соответственно.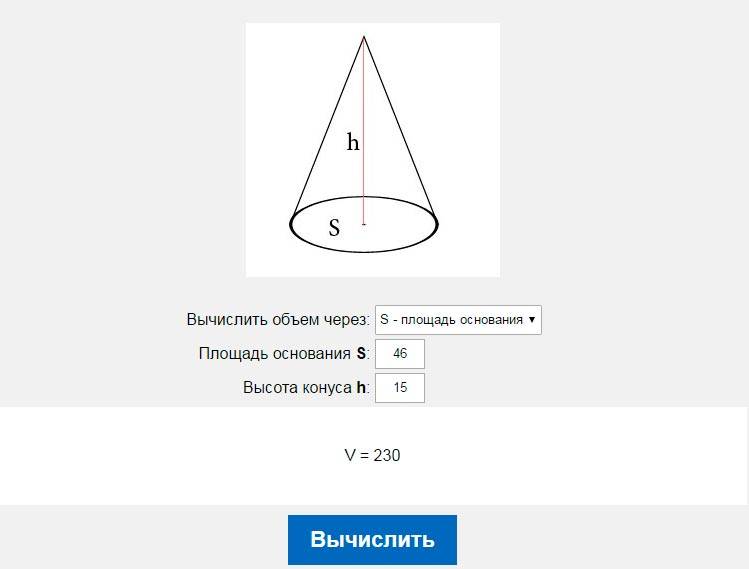
Более точной единицей измерения для полученных значений будет не «пиксель», а скорее сторона пикселя, поскольку пиксель представляет собой квадрат определенной площади и для измерения длин не очень подходит.
Подсчитаем площадь комнаты в пикселях:
Далее, введем коэффициент, который будет показывать насколько отличается длина стороны пикселя нашего изображения от длины квадратного метра. Обозначим этот коэффициент буквой «k».
Искомые значения длины и ширины комнаты, будут найдены по формуле:
Остается выяснить чему равен коэффициент. Для этого составим простое уравнение, из которого элементарно находим значение коэффициента, как корень из соотношения площадей в пикселях и в квадратных метрах.
Подставляем значение найденного коэффициента в формулы для нахождения длины и ширины комнаты и получаем искомые величины.
Зная коэффициент, мы можем получить длину в метрах для любого объекта в имеющемся плане.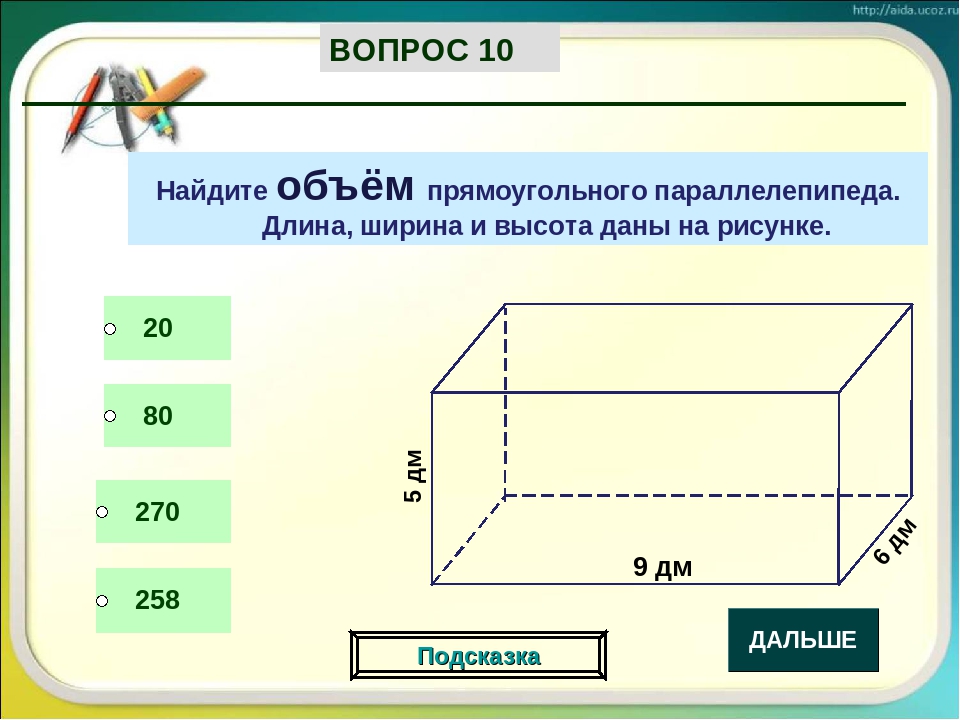 Нужно только узнать длину этого объекта в пикселях и умножить полученное значение на коэффициент.
Нужно только узнать длину этого объекта в пикселях и умножить полученное значение на коэффициент.
Обращаю внимание, что значение вычисленного коэффициента подходит только для данного конкретного изображения, из которого этот коэффициент вычислялся. Если возьмете другое изображение, то коэффициент придется считать заново.
На этом все, если остались вопросы, оставляйте их в комментариях к статье.
Вычисление формулы объема и площади в Excel
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. 3 (A2 – это ссылка на ячейку).
3 (A2 – это ссылка на ячейку).
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.
Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.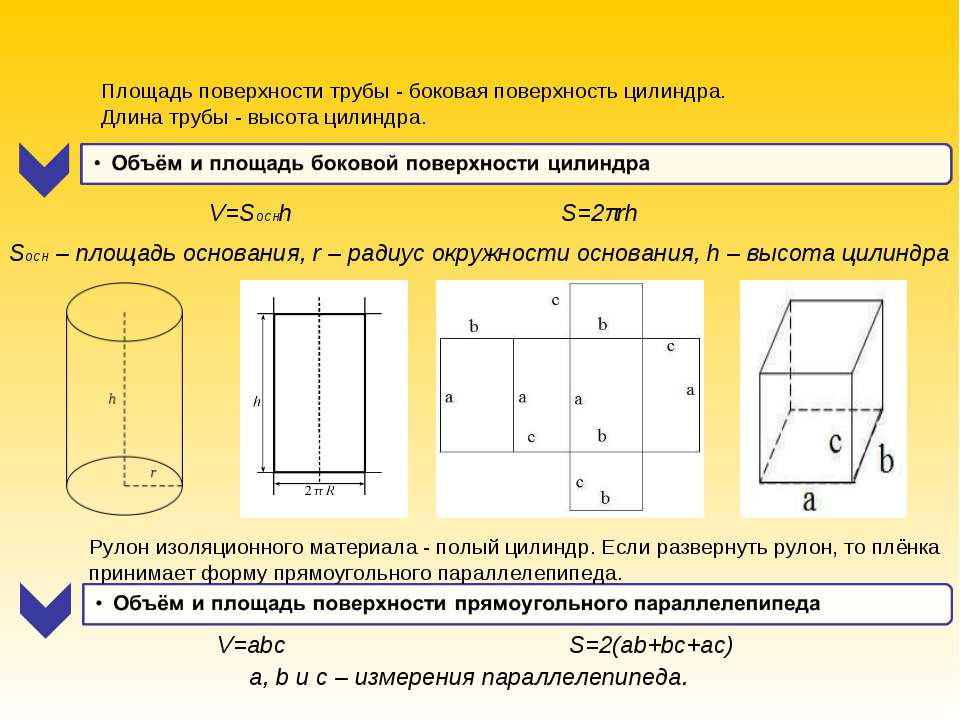
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Давайте вспомним, какие виды параллелепипедов бывают.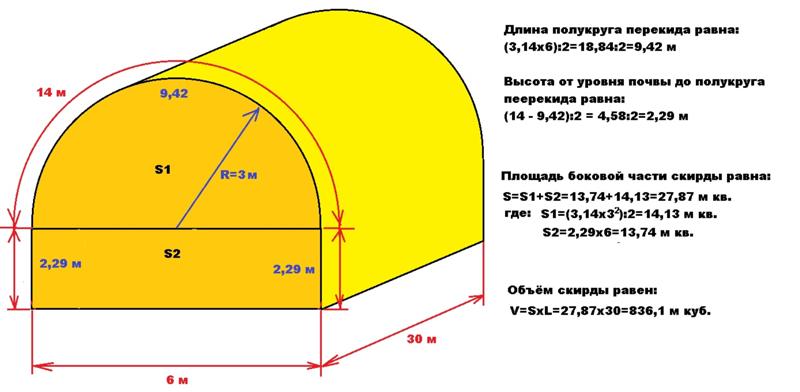
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.
Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.
Какие бывают призмы:
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a * b * h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.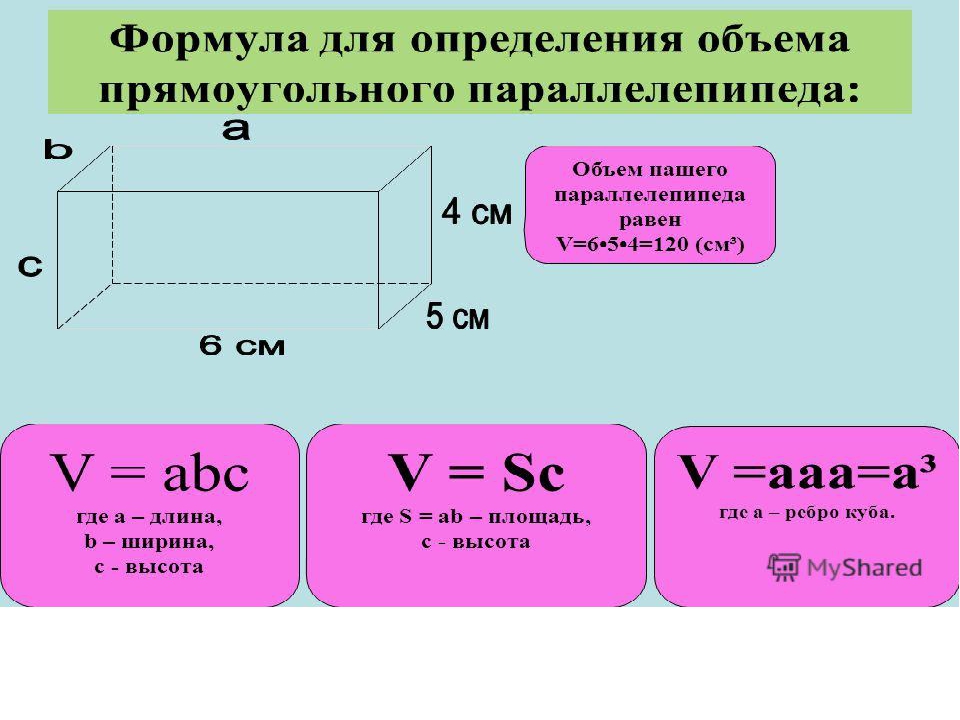
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п.п.) | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a * b * h
V = 9 * 6 * 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие 1 Объем параллелепипеда равен произведению площади основания на высоту. V = S осн * h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
S осн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 82 см3, а высота 8 см.
V = 82 см3
h = 8 см
V = S осн * h
S осн = V : h
S осн = 82 см3: 8 см = 10,25 см2.
Ответ: площадь основания параллелепипеда равна 10,25 см2.
Следствие 2 Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. V = S осн * h |
Пример 3. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 и 8 см.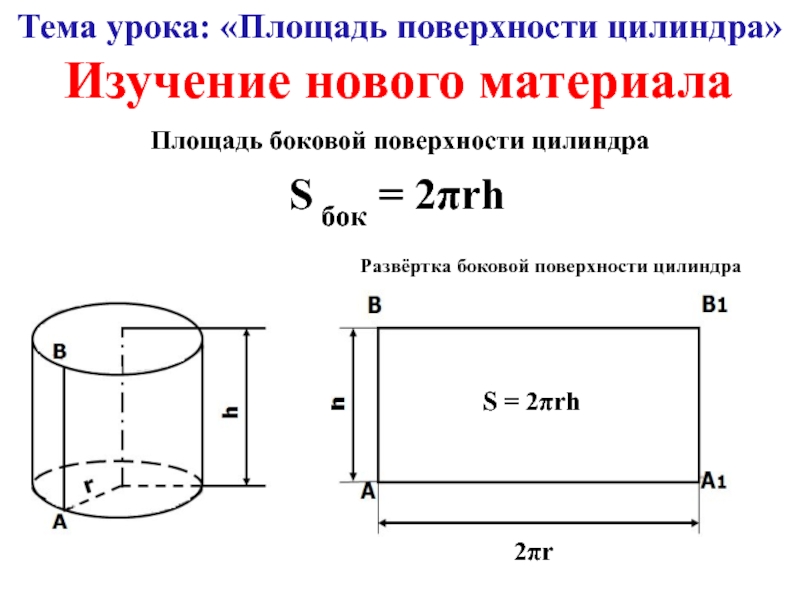 Боковое ребро равно 5. Найдем объем призмы.
Боковое ребро равно 5. Найдем объем призмы.
V = S * h = 12* a * b * h
a = 6
b = 8
h = 5
V = 1/2 * 6 * 8 * 5 = 120 см3.
Ответ: объём прямой призмы, основанием которой является прямоугольный треугольник, равен 120 см3.
С каждым годом геометрия становится все более объемной. Формулы множатся, а задачки усложняются. В детской онлайн-школе Skysmart ваш ребенок сможет заполнить пробелы, разобрать сложные темы и научиться доказывать любые теоремы.
Записывайтесь на бесплатный вводный урок и знакомьтесь с устройством учебной платформы лично.
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания.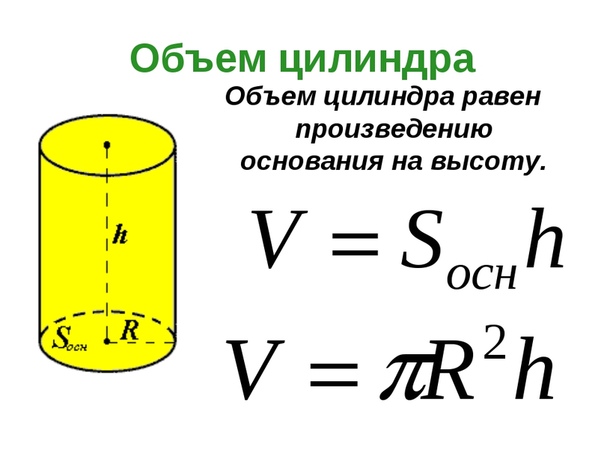
- S п.п. = 2 (ab + ac + bc)
Пример 4. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
S п.п. = 2 (ab + ac + bc)
S п.п. = 2(6 * 4 + 6 * 3 + 4 * 3) = 2 * (24 + 18 + 12) = 2 * 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно. В интернете есть много онлайн-калькуляторов, которые помогут вам быстро вычислить объем:
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a * b * h
Подставляем наши числа:
V = 18 * 10 * 7 = 1260 см3.
Ответ: объём параллелепипеда = 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём = 120 см3, а высота — 15 см.
Как решаем:
V = 120 см3
h = 15 см
V = S осн * h
S осн = V : h
S осн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда = 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания = 30 сантиметров, ширина = 12 см, а высота = 5 см.
Как решаем:
S п.п. = 2 (ab + ac + bc)
S п.п. = 2(30 * 12 + 30 *5 + 12 * 5) = 2 * (360 + 150 + 60) = 2 * 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда = 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a * b * h |
| V = S осн * h |
S боковой поверхности | S б. |
S полной поверхности | S п.п. = 2 (ab + ac + bc) |
Диагональ параллелепипеда | d2 = a2+ b2 + c2 |
На уроках математики в современной школе Skysmart нет скучных учебников, надоевших задачек и неинтересных тетрадей. Ученики занимаются по интерактивному учебнику, чертят на настоящей онлайн-доске и решают занимательные примеры.
Математика может быть по-настоящему увлекательной. Записывайтесь на бесплатный вводный урок, чтобы проверить, так ли это на самом деле.
Как найти объем, зная площадь
Объем геометрической фигуры — один из ее параметров, количественно характеризующий пространство, которое эта фигура занимает. У объемных фигур есть и другой параметр — площадь поверхности. Эти два показателя связаны между собой определенными соотношениями, что позволяет, в частности? рассчитать объем правильных фигур, зная площадь их поверхности.
Площадь поверхности сферы (S) может быть выражена как учетверенное произведение числа Пи на возведенный в квадрат радиус (R): S = 4*π*R². Объем (V) шара, ограниченного этой сферой, тоже может быть выражен через радиус — он прямо пропорционален произведению учетверенного числа Пи на радиус, возведенный в куб, и обратно пропорционален тройке: V = 4*π*R³/3. Используйте эти два выражения, чтобы получить формулу расчета объема, связав их через радиус — выразите радиус из первого равенства (R = ½*√(S/π)) и подставьте его во второе тождество: V = 4*π*(½*√(S/π))³/3 = ⅙*π*(√(S/π))³.
Аналогичную пару выражений можно составить для площади поверхности (S) и объема (V) куба, связав их через длину ребра (a) этого многогранника. Объем равен третьей степени длины ребра (√ = a³), а площадь поверхности — увеличенной в шесть раз второй степени этого же параметра фигуры (V = 6*a²). Выразите длину ребра через площадь поверхности (a = ³√V) и подставьте в формулу расчета объема: V = 6*(³√V)².
Объем сферы (V) можно вычислить и по площади не полной поверхности, а лишь отдельного сегмента (s), высота которого (h) тоже известна. Площадь такого участка поверхности должна быть равна произведению удвоенного числа Пи на радиус сферы (R) и высоту сегмента: s = 2*π*R*h. Найдите из этого равенства радиус (R = s/(2*π*h)) и подставьте в формулу, связывающую объем с радиусом (V = 4*π*R³/3). В результате упрощения формулы у вас должно получиться такое выражение: V = 4*π*(s/(2*π*h))³/3 = 4*π*s³/(8*π³*h³)/3 = s³/(6*π²*h³).
Площадь такого участка поверхности должна быть равна произведению удвоенного числа Пи на радиус сферы (R) и высоту сегмента: s = 2*π*R*h. Найдите из этого равенства радиус (R = s/(2*π*h)) и подставьте в формулу, связывающую объем с радиусом (V = 4*π*R³/3). В результате упрощения формулы у вас должно получиться такое выражение: V = 4*π*(s/(2*π*h))³/3 = 4*π*s³/(8*π³*h³)/3 = s³/(6*π²*h³).
Для вычисления объема куба (V) по площади одной его грани (s) никаких дополнительных параметров знать не требуется. Длину ребра (a) правильного гексаэдра можно найти извлечением квадратного корня из площади грани (a = √s). Подставьте это выражение в формулу, связывающую объем с размером ребра куба (V = a³): V = (√s)³.
Объем прямоугольных призм — объяснения и примеры
Объем прямоугольной призмы — это мера пространства, которое она заполняет. В этой статье вы узнаете , как найти объем прямоугольной призмы, используя формулу объема прямоугольной призмы . Мы также обсудим объем сферического цилиндра.
Как найти объем прямоугольной призмы?
Прямоугольная призма — это трехмерный объект с шестью прямоугольными гранями .Прямоугольную призму также называют кубоидом, прямоугольным шестигранником, правой прямоугольной призмой или прямоугольным параллелепипедом.
Чтобы найти объем прямоугольной призмы, умножьте длину, ширину и высоту. Единица измерения объема прямоугольной призмы — кубические единицы, т.е. см 3 , мм 3 , в 3 , м 3, и т. Д.
Формула объема прямоугольной призмы
Формула объема прямоугольной призмы имеет вид:
Объем прямоугольной призмы = (длина x ширина x высота) кубических единиц.
V = (длина x ширина x высота) кубических единиц
В прямоугольной призме произведение длины и ширины называется площадью основания. Следовательно, мы также можем представить объем прямоугольной призмы по формуле:
Объем прямоугольной призмы = Базовая площадь x высота
Давайте попробуем формулу, решив несколько примеров задач.
Пример 1
Длина, ширина и высота прямоугольной призмы составляют 15 см, 10 см и 5 см соответственно.Каков объем призмы?
Решение
Дано, длина = 15 см,
ширина = 10 см,
высота = 5 см.
По объему прямоугольной призмы имеем
Объем = l x w x h
= (15 x 10 x 5) см 3
= 750 см 3 .
Пример 2
Объем прямоугольной призмы 192 см 3 . Если длина призмы в два раза больше высоты и ширины 6 см, найдите размеры прямоугольной призмы.
Решение
Дано,
Пусть высота равна x.
Длина = 2x
Ширина = 6 см.
Объем = 192.
По объему прямоугольной призмы
⇒ 192 = x (2x) (6)
⇒ 192 = 12x 2
Разделив обе стороны на 12, получим
⇒ 16 = x 2
⇒ x = 4, -4
Заменитель
Длина = 2x ⇒ 2x 4 = 8 см
Высота = x ⇒ 4 см
Следовательно, размеры прямоугольной призмы составляют 8 см, 6 см и 4 см.
Пример 3
Длина и ширина прямоугольного аквариума составляет 800 мм и 350 мм. Когда рыбу заводят в аквариум, уровень воды поднимается на 150 мм. Найдите объем рыбы.
Раствор
Объем рыбы = объем вытесненной воды.
Объем рыбы = 800 x 350 x 150 мм 3
= 4,2 x 10 7 мм 3
Пример 4
Прямоугольный резервуар для воды длиной 80 м, 50 м шириной и высотой 60 м.Если глубина воды в резервуаре составляет 45 м, найти объем воды, необходимый для заполнения резервуара?
Раствор
Чтобы найти объем воды, необходимый для заполнения бака, вычтите доступный объем воды из объема воды, когда бак заполнен.
Объем воды при полном баке = 80 x 50 x 60
= 240000 м 3
Объем имеющейся воды = 80 x 50 x 45
= 180000 м 3
Объем воды требуемая вода = (240 000 — 180 000) м 3
= 60 000 м 3
Пример 5
Объем и базовая площадь прямоугольного грузового контейнера составляет 778 м 3 и 120 м 2 .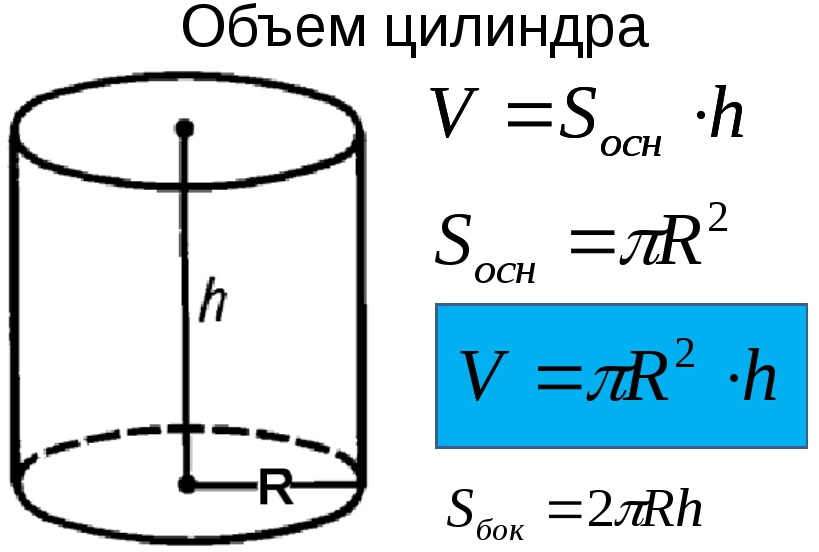 Найдите высоту контейнера?
Найдите высоту контейнера?
Раствор
Объем прямоугольной призмы = площадь основания x высота
778 = 120 x высота
Разделите 120 с обеих сторон.
778/120 = высота
высота = 6,48 м
Итак, высота контейнера составляет 6,48 м.
Пример 6
Маленькие коробки размером 1 м x 4 м x 5 м должны быть упакованы в больший прямоугольный контейнер размером 8 м x 10 м x 5 м.Найдите максимальное количество коробок, которое можно упаковать в контейнер?
Раствор
Чтобы найти количество коробок, которые нужно упаковать, разделите объем контейнера на объем коробки.
Объем контейнера = 8 x 10 x 5
= 400 м 3 .
Объем ящика = 1 x 4 x 5
= 20 м 3
Количество ящиков = 400 м 3 /20 м 3 .
= 20 коробок.
Пример 7
Внешние размеры открытого сверху деревянного ящика составляют 12 см в длину, 10 см в ширину и 5 см в высоту. Если стенки коробки имеют толщину 1 см, найдите объем коробки
Если стенки коробки имеют толщину 1 см, найдите объем коробки
Решение
Найдите внутренние размеры коробки
Длина = 12 — (1 x 2)
= 10 см
Ширина = 10 — (1 x 2)
= 8 см
Высота = 5 см — 1 …… (открыто вверху)
= 4 см
Объем = 10 x 8 x 4
= 320 см 3 .
Пример 8
Каковы размеры куба того же объема, что и прямоугольная призма с размерами 8 м на 6 м на 3 м?
Раствор
Объем прямоугольной призмы = 8 x 6 x 3
= 144 см 3
Таким образом, куб также будет иметь объем 144 см 3
Поскольку мы знаем, что объем куба = a 3
, где a — длина куба.
144 = a 3
3 √ a 3 = 3 √144
a = 5,24
Таким образом, размеры куба будут 5,24 см на 5,24 см на 5,24 см.
Пример 9
Рассчитайте объем твердой прямоугольной призмы, площадь основания которой составляет 18 дюймов 2 и высота 4 дюйма
Решение
Объем прямоугольной призмы = длина x ширина x высота
= площадь основания x высота
V = 18 x 4
= 72 дюйма 3 .
Пример 10
Найдите площадь основания прямоугольной призмы объемом 625 см 3 и высотой 18 см.
Решение
Объем = площадь основания x высота
625 = площадь основания x 18
Разделив обе стороны на 18, мы получим
Площадь основания = 34,72 см 2
Практические вопросы
- Как определить призму?
А.Он имеет одинаковую или неодинаковую длину, высоту и ширину.
Б. Имеет неравную длину, высоту и ширину.
C. Он имеет одинаковую или неодинаковую длину, высоту и ширину.
D. Ничего из этого.
2. Что из следующего не является призмой?
A. Ящик для салфеток
B. Футбол
C. Dice
D. Ни один из этих
3. Сколько кубических метров воды может вместить бассейн в форме прямоугольной призмы длиной 12 метров 5 метров шириной и 1.5 метров глубиной?
4. У Джеймса есть музыкальная шкатулка высотой 12,5 см и площадью основания 75 см2. Найдите объем музыкальной шкатулки.
Найдите объем музыкальной шкатулки.
Ответы
- C
- B
- 90 кубических метров
- 5 кубических см
Предыдущий урок | Главная страница | Следующий урок
Математические формулы для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм.Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур. Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь и объем сферы
Д. Рассел
Трехмерный круг известен как сфера. Чтобы вычислить площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ).Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. Рассел
Рассел
Конус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь и объем цилиндра
Д. Рассел
Вы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. Рассел
Прямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для этого вам нужно знать длину ( х ), высоту ( х ) и ширину ( х ).С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (левый) + 2 (левый) + 2 (белый)
- Объем = lhw
Площадь и объем пирамиды
Д. Рассел
Рассел
С пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 б 2 ч
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д.Рассел
При переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину ( l ) формы. Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих вычислений.
Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих вычислений.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (бч) л
Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле будет использоваться высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = объявления
Площадь сектора круга
Д. Рассел
Площадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. Рассел
Эллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Semiminor Axis ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете увидеть эту формулу, записанную с r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам нужно будет знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, который имеет одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга. Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольника, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ), это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были соединены как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник — это тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).
- Периметр = 2h + 2w
- Площадь = в x ш
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать только длину одной стороны ( с ), чтобы определить ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
Как определить объем трехмерных объектов [Видео]
Как рассчитать объем трехмерных объектов
Привет, ребята.Добро пожаловать в этот видеоролик, посвященный объему трехмерных объектов.
Начнем с определения объема. Объем — это измерение того, сколько места занимает жидкость или газ, или сколько места жидкость или газ занимают в данном объекте.
Возможно, вы этого не знаете, но люди используют громкость каждый день. Объем используется для расчета количества питья. Количество воды, которое вы можете удерживать в чашке, зависит от ее объема. Есть несколько других способов использования громкости.
Теперь давайте посмотрим, как рассчитать объем треугольной призмы, прямоугольной призмы, сферы и конуса.
Объем треугольной призмы:
Площадь треугольника равна \ (A = \ frac {1} {2} bh \). По сути, чтобы найти объем треугольной призмы, вы умножаете площадь треугольника на длину или глубину. Итак, формула для объема треугольной призмы будет \ (V = \ frac {1} {2} bhl \).
По сути, чтобы найти объем треугольной призмы, вы умножаете площадь треугольника на длину или глубину. Итак, формула для объема треугольной призмы будет \ (V = \ frac {1} {2} bhl \).
Давайте посмотрим:
У нас есть треугольная призма высотой 8 метров, основанием 13 метров и длиной 4 метра.{3} \). Важно знать, что при работе с объемом у нас всегда будут кубические единицы, потому что мы умножаем единицы сами на себя 3 раза.
Объем куба или прямоугольной призмы:
Чтобы найти такой же объем куба или прямоугольной призмы, воспользуйтесь той же формулой.
Как и в случае с треугольной призмой, вам нужно найти площадь одной стороны, а затем умножить ее на длину. Однако важно знать, что формула, которую вы используете для определения площади треугольника, отличается от формулы, которую вы используете для определения площади квадрата или прямоугольника.
Формула площади квадрата и прямоугольника: \ (A = b h \). Итак, чтобы найти объем куба или прямоугольной призмы, вы должны найти площадь квадрата или прямоугольника, а затем умножить ее на длину. {2} \).{3} \). Когда вы делаете то, что называется доказательством, чтобы доказать, что это формула, а пока мы просто подставим числа в данную формулу.
{2} \).{3} \). Когда вы делаете то, что называется доказательством, чтобы доказать, что это формула, а пока мы просто подставим числа в данную формулу.
Сфера имеет диаметр 20 метров. Это вся информация, которая нам нужна для решения нашего уравнения. Мы ищем радиус, и мы знаем, что радиус равен половине диаметра, что означает, что наш радиус равен 10 метрам. Когда мы подставляем 10 в нашу формулу и решаем, мы получаем 4 188,9 метра в кубе.
Объем конуса:
Формула для объема конуса очень похожа на формулу для площади круга.{3} \).
Отличная работа, ребята. Изучение новых формул может быть трудным. Важно продолжать практиковаться, чтобы вы могли распознать, какую формулу вам нужно использовать, и запомнить формулы.
Надеюсь, это было полезно. Не забудьте проверить больше наших видео, подписавшись ниже. Увидимся в следующий раз!
Объем призмы
А
призма
многогранник с двумя параллельными конгруэнтными гранями, называемыми основаниями, которые
полигоны
.
В
объем
из
3
-размерное твердое тело — это объем занимаемого пространства.Объем измеряется в кубических единицах (
в
3
,
футов
3
,
см
3
,
м
3
и так далее). Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.
Громкость
V
призмы — это площадь основания
B
раз больше высоты
час
.
V
знак равно
B
час
Примечание:
Кубический сантиметр (
см
3
) — куб, ребра которого измеряют
1
сантиметр.
Пример:
Найдите объем показанной призмы.
Решение
Формула объема призмы:
V
знак равно
B
час
, где
B
это базовая площадь и
час
это высота.
Основание призмы — прямоугольник.Длина прямоугольника
9
см и ширина
7
см.
Площадь
А
прямоугольника длиной
л
и ширина
ш
является
А
знак равно
л
ш
.
Итак, базовая площадь равна
9
×
7
или же
63
см
2
.
Высота призмы
13
см.
Заменять
63
для
B
а также
13
для
час
в
V
знак равно
B
час
.
V
знак равно
(
63
)
(
13
)
Умножить.
V
знак равно
819
Следовательно, объем призмы равен
819
кубические сантиметры.
1.4: Объем, толщина и плотность
Цели обучения
- Вычислить площадь, объем, плотность и толщину и преобразовать в различные единицы.
Производные единицы СИ
Мы можем вывести многие единицы из семи основных единиц СИ.Например, мы можем использовать базовую единицу длины для определения единицы объема, а базовые единицы массы и длины — для определения единицы плотности.
Том
Объем — это мера пространства, занимаемого объектом. Стандартная единица объема в системе СИ определяется базовой единицей длины (рисунок \ (\ PageIndex {3} \)). Стандартный объем — кубический метр ( 3 м), куб с длиной ребра ровно один метр. Чтобы распределить кубический метр воды, мы могли бы построить кубический ящик с длиной кромки ровно один метр.В этом ящике помещался кубический метр воды или любого другого вещества.
Стандартная единица объема в системе СИ определяется базовой единицей длины (рисунок \ (\ PageIndex {3} \)). Стандартный объем — кубический метр ( 3 м), куб с длиной ребра ровно один метр. Чтобы распределить кубический метр воды, мы могли бы построить кубический ящик с длиной кромки ровно один метр.В этом ящике помещался кубический метр воды или любого другого вещества.
Более часто используемая единица объема — дециметр (0,1 м или 10 см). Куб с длиной ребер ровно один дециметр содержит объем в один кубический дециметр (дм 3 ). Литр (L) — более распространенное название кубического дециметра. Один литр составляет около 1,06 кварты. Кубический сантиметр ( 3 см) — это объем куба с длиной ребра ровно один сантиметр. Аббревиатура cc (для c ubic c entimeter) часто используется медицинскими работниками.Кубический сантиметр также называется миллилитром (мл) и составляет 1/1000 литра.
< Рисунок \ (\ PageIndex {3} \): (a) Относительные объемы показаны для кубов размером 1 м 3 , 1 дм 3 (1 л) и 1 см 3 (1 мл) (не в масштабе). (b) Диаметр десятицентовика сравнивается с длиной ребра куба размером 1 см 3 (1 мл).
Плотность
Мы используем массу и объем вещества для определения его плотности. Таким образом, единицы плотности определяются основными единицами массы и длины.
Плотность вещества — это отношение массы образца вещества к его объему. Единица измерения плотности в системе СИ — килограмм на кубический метр (кг / м 3 ). Однако для многих ситуаций это неудобная единица измерения, и мы часто используем граммы на кубический сантиметр (г / см 3 ) для плотности твердых веществ и жидкостей и граммы на литр (г / л) для газов. Хотя есть исключения, большинство жидкостей и твердых веществ имеют плотность в диапазоне от примерно 0,7 г / см 3 (плотность бензина) до 19 г / см 3 (плотность золота).Плотность воздуха около 1,2 г / л. В таблице \ (\ PageIndex {3} \) показаны плотности некоторых распространенных веществ.
| Твердые вещества | Жидкости | Газы (при 25 ° C и 1 атм) |
|---|---|---|
| лед (при 0 ° C) 0,92 г / см 3 | вода 1.0 г / см 3 | сухой воздух 1,20 г / л |
| дуб (дерево) 0,60–0,90 г / см 3 | этанол 0,79 г / см 3 | кислород 1,31 г / л |
| железо 7,9 г / см 3 | ацетон 0,79 г / см 3 | азот 1,14 г / л |
| медь 9,0 г / см 3 | глицерин 1.26 г / см 3 | диоксид углерода 1,80 г / л |
| свинец 11,3 г / см 3 | оливковое масло 0,92 г / см 3 | гелий 0,16 г / л |
| серебро 10,5 г / см 3 | бензин 0,70–0,77 г / см 3 | неон 0,83 г / л |
| золото 19,3 г / см 3 | ртуть 13.6 г / см 3 | радон 9,1 г / л |
Хотя есть много способов определить плотность объекта, возможно, самый простой метод включает в себя раздельное определение массы и объема объекта с последующим делением массы образца на его объем. В следующем примере масса определяется непосредственно путем взвешивания, а объем определяется косвенно путем измерения длины.
\ [\ mathrm {density = \ dfrac {mass} {volume}} \]
Пример \ (\ PageIndex {1} \)
Расчет плотности Золото — в кирпичах, слитках и монетах — веками было формой валюты.Чтобы обманом заставить людей платить за кирпич из золота, не вкладывая деньги в кирпич из золота, люди рассматривали возможность заполнения центров пустотелых золотых кирпичей, чтобы заставить покупателей думать, что весь кирпич — золото. Не работает: свинец — плотное вещество, но его плотность не такая большая, как у золота, 19,3 г / см 3 . Какова плотность свинца, если кубик свинца имеет длину ребра 2,00 см и массу 90,7 г?
Решение
Плотность вещества можно рассчитать, разделив его массу на его объем.3} \]
Упражнение \ (\ PageIndex {1} \)
- С точностью до трех десятичных знаков, каков объем куба (см 3 ) с длиной ребра 0,843 см?
- Если куб в части (а) состоит из меди и имеет массу 5,34 г, какова плотность меди с точностью до двух знаков после запятой?
- Ответьте на
0,599 см 3 ;
- Ответ б
8,91 г / см 3
Пример \ (\ PageIndex {2} \): Использование вытеснения воды для определения плотности
Это моделирование PhET иллюстрирует другой способ определения плотности с использованием вытеснения воды.Определите плотность красных и желтых блоков.
Решение
Когда вы открываете моделирование плотности и выбираете Same Mass, вы можете выбрать один из нескольких цветных блоков весом 5,00 кг, которые вы можете бросить в резервуар, содержащий 100,00 л воды. Желтый блок плавает (он менее плотный, чем вода), а уровень воды поднимается до 105,00 л. Во время плавания желтый блок вытесняет 5,00 л воды, количество, равное весу блока. Красный блок тонет (он плотнее воды, плотность которой = 1.00 кг / л), а уровень воды поднимается до 101,25 л.
Красный блок, таким образом, вытесняет 1,25 л воды, количество, равное объему блока. Плотность красного блока:
\ [\ mathrm {density = \ dfrac {mass} {volume} = \ dfrac {5.00 \: kg} {1.25 \: L} = 4.00 \: kg / L} \]
Обратите внимание, что, поскольку желтый блок не полностью погружен в воду, вы не можете определить его плотность по этой информации. Но если удерживать желтый блок на дне емкости, уровень воды поднимется до 110.00 л, что означает, что теперь он вытесняет 10,00 л воды, а его плотность можно определить:
\ [\ mathrm {density = \ dfrac {масса} {объем} = \ dfrac {5.00 \: кг} {10.00 \: L} = 0.500 \: кг / л} \]
Упражнение \ (\ PageIndex {1} \)
Удалите все блоки из воды и добавьте зеленый блок в резервуар с водой, поместив его примерно посередине резервуара. Определите плотность зеленого блока.
- Ответ
2,00 кг / л
Толщина
Ширина объекта также иногда определяется как толщина (T).Обычно это происходит, когда ширина объекта значительно меньше других размеров. Для измерения толщины требуется инструмент с высокой точностью, например штангенциркуль. Однако, если вы знаете площадь, массу и плотность вещества, вы можете рассчитать толщину.
Используйте эту формулу для расчета толщины: \ (\ mathrm {Thickness = \ dfrac {volume} {area}} \)
Чтобы найти объем, вам нужно изменить формулу плотности. \ (\ mathrm {volume = \ dfrac {mass} {density}} \)
Пример \ (\ PageIndex {2} \): расчет толщины
Кусок алюминиевой фольги имеет массу 0.018 г и по 5,0 см с каждой стороны. Какова толщина алюминия в сантиметрах, учитывая плотность алюминия 2,7 г / куб.
Решение
\ (\ mathrm {толщина = \ dfrac {volume} {area}} \)
Сначала найдите объем фольги.
\ [\ mathrm {volume = \ dfrac {mass} {density} = \ dfrac {0.018 \: g} {2.7 \: g / cc} = 0.00667 \: cc} \]
Затем найдите область фольги.
\ [\ mathrm {area = 5.0 \: см \ times5.2} = 0,00027 \: см} \]
Сводка
Ученые используют производные единицы, такие как литры (для объема) и г / см. 3 (для плотности). Толщина — это способ выразить ширину объекта, когда этот размер невелик.
Ключевые уравнения
- \ (\ mathrm {density = \ dfrac {mass} {volume}} \)
- \ (\ mathrm {толщина = \ dfrac {volume} {area}} \)
Глоссарий
- плотность
- отношение массы к объему вещества или объекта
- литр (л)
- (также кубический дециметр) единица объема; 1 L = 1000 см 3
- миллилитр (мл)
- 1/1000 литра; равно 1 см 3
- секунд
- СИ единица времени
- единиц СИ (Международная система единиц)
- стандартов, установленных международным соглашением в Международной системе единиц ( Le Système International d’Unités )
- толщина
- другой способ выразить ширину объекта, которую можно вычислить, разделив объем объекта на площадь.
- том
- место, занимаемое объектом
Площадь поверхности и объем пирамид, призм, цилиндров и конусов (Геометрия, Площадь) — Mathplanet
Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела.Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.
Объем — это мера того, сколько может вместить фигура, и измеряется в кубических единицах. Объем говорит нам кое-что о вместимости фигуры.
Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть как прямоугольные, так и треугольные призмы.
Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем твердое тело, как картонную коробку, и расплющиваем его, чтобы найти все включенные геометрические формы.
Чтобы найти объем призмы (не имеет значения, прямоугольная она или треугольная), мы умножаем площадь основания, называемую площадью основания B, на высоту h.
$$ V = B \ cdot h $$
Цилиндр — это труба, состоящая из двух параллельных конгруэнтных окружностей и прямоугольника, основанием которого является окружность окружности.{2} \ cdot h $$
Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех- или четырехсторонней поверхности соответственно в основании. Когда мы вычисляем площадь поверхности пирамиды ниже, мы берем сумму площадей четырех треугольников и базового квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.
Объем пирамиды составляет одну треть объема призмы.
$$ V = \ frac {1} {3} \ cdot B \ cdot h $$
Основание конуса — круг, и это легко увидеть.{3}
$
Видеоурок
Найти площадь поверхности цилиндра радиуса 4 и высоты 8
Найти объем конуса высотой 5 и радиусом 3
чисел — объем — треугольные призмы
Введение
Бывают ситуации, когда вам необходимо рассчитать объем треугольной призмы .Это может быть треугольный разрез на бетонной плите или выемка грунта из наклонного блока.
Вы знаете, как рассчитать объем треугольных призм?
Расчетный объем
Помните, что формула для расчета объема:
V olume = A rea на h восемь
V = A X h .
Для треугольника площадь рассчитывается по формуле:
A rea = половина b ase на a ltitude
A = 0.5 X b X a .
Итак, чтобы рассчитать объем треугольной призмы , формула:
V = 0,5 X b X a X h .
Упражнение 1
Вычислите объем треугольной призмы.
Введите свой ответ и выберите «Отправить» для отзыва.
м 3
Представлять на рассмотрение
Упражнение 2
Вычислите объем треугольной призмы.
Введите свой ответ и выберите «Отправить» для отзыва.
м 3
Представлять на рассмотрение
Упражнение 3
Вычислите объем треугольной призмы.
Введите свой ответ и выберите «Отправить» для отзыва.
м 3
Представлять на рассмотрение
Упражнение 4
Вычислите объем треугольной призмы.
Введите свой ответ и выберите «Отправить» для отзыва.
м 3
Представлять на рассмотрение
Сводка
Это конец раздела о треугольных призмах.
Ключевые моменты, о которых следует помнить:
- формула объема:
Объем = Площадь по высоте - рассчитайте объем треугольной призмы по формуле:
Объем = половина базы по высоте по высоте.
Вы можете просмотреть этот раздел или выбрать другой в левом меню.

 п. = 2(ac + bc)
п. = 2(ac + bc)