Калькулятор кубов онлайн: Калькулятор кубов

22.11.2021 0 Разное

Содержание

Калькулятор онлайн

1234567890Ввод цифр
±Изменение знака на противоположный
.Отделение дробной части в десятичной дроби
CОчистка
=Вычисление
⇦Отмена последнего изменения
⇆Перемещение курсора в области ввода
+−×÷Основные операции: сложение, вычитание, умножение, деление Пример
2+3=
÷Разделение двух частей обыкновенной дроби Пример
5÷8−1÷4=
()Ввод скобок Пример
(2+2)×2=
,Разделение аргументов функции или элементов массива
1/xНахождение обратного числа Пример
51/x=
eВвод математической константы e
iВвод мнимой единицы. (Эта кнопка появляется после длительного нажатия на кнопку e)
%1) Нахождение процента от числа, 2) Изменение числа на процент. (Эта кнопка появляется после длительного нажатия на кнопку 1/x) Пример

1) 40×5%=

2) 40−5%=

x2x3xy10XВозведение в степень Пример
3x2=
2xy4=
510X=
√x3√xy√xКорень из числа Пример
1253√x=
16y√x4=
logЛогарифм Пример
log16,2=

Сумма двух кубов: онлайн калькулятор, формула, вычисления с примерами

Сумма двух кубов – это формула сокращенного умножения, позволяющие преобразовывать и упрощать математические выражения.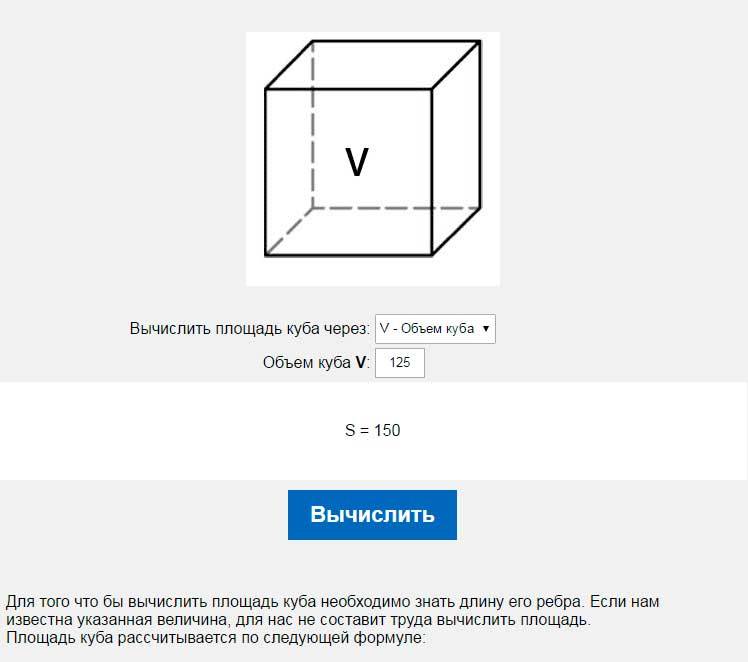 Формулы сокращенного умножения постоянно используются при развязывании уравнений или решении алгебраических, тригонометрических, логарифмических и показательных выражений.

Историческая справка

Некоторые формулы сокращенного умножения были составлены еще в четвертом тысячелетии до нашей эры древними вавилонянами. Древние греки развили идеи вавилонских ученых и разработали целый набор подобных формул. Однако античные математики мыслили зримо – в то время числа визуализировались в геометрических фигурах или подручных предметах, например, камнях на счетной доске. Формулы суммы квадратов выводились не алгебраически, а геометрически, путем рассечения плоского квадрата на части. Расцвет математической науки пришелся на времена Лейбница, Ньютона и Эйлера и именно эти ученые внесли большой вклад в развитие формул сокращенного умножения.

Сумма двух кубов

Алгебраический куб – это возведение числа или неизвестного в третью степень. Следовательно, сумма двух кубов – это результат сложения двух чисел в третьей степени. Записывается это следующим образом:

a3 + b3

Такой пример решается довольно просто, но при любых значениях a и b ответ можно представить в виде:

(a + b) × (a2 − ab + b2).

Следовательно, у нас есть тождество, которое работает при любых значениях переменных:

a3 + b3 = (a + b) × (a2 − ab + b2).

Доказать его можно простым раскрытием скобок и сокращением членов в правой части выражения. Данное тождество используется для сокращения выражений и быстрого поиска ответов или для разложения на множители.

Вряд ли подобные формулы понадобятся нам в реальной повседневности, но школьникам крайне важно знать формулы сокращенного умножения наизусть. Простыми словами формула звучит так: сумма двух кубов есть произведение суммы членов выражения на неполный квадрат их разности. Словосочетание «неполный» квадрат может вызвать у ребят сомнения. Полный квадрат разности – это еще одна формула сокращенного умножения, которая выглядит так:

(a − b)2 = a2 − 2ab + b2

В левой части у нас квадрат разности a – b, а справа – полный квадрат, разложенный на множители.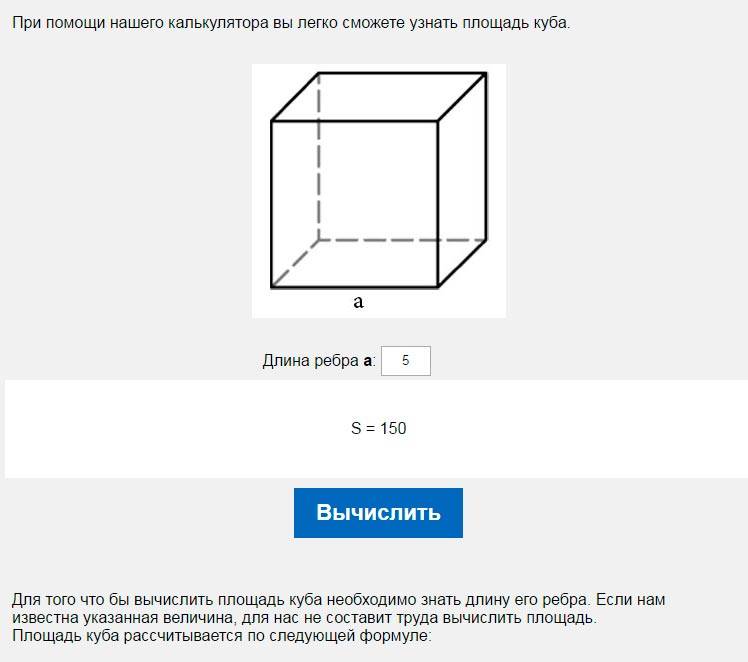 Выражение a2 – ab + b2 для суммы двух кубов носит название неполного, так как в нем произведение ab без двойки. Данные тождества используются для упрощения громоздких выражений, а также для проверки полученных результатов сложения кубов или квадратов больших чисел.

Применение формулы на практике

Сумма двух кубов используется на практике для упрощения многочленов. Например, у нас есть сложный тригонометрический пример:

(sinx + cosy) × (sin2 x − sinx × cosy + cos2 y)

Решать этот пример при помощи тригонометрического аппарата было бы довольно сложно, особенно для школьника, незнакомого со свойствами синусов и косинусов. Однако мы можем применить правило суммы двух кубов, ведь данный пример полностью повторяет разложение на множители выражения a2 + b2, только здесь a = sinx, b = cosy. В итоге громоздкое тригонометрическое выражение превратится в компактную запись:

sin3 x + cos3 y.

Теперь давайте применим эту формулу при счете. Большинство людей практически наизусть знает квадраты натуральных чисел до 15, а те, кто постоянно занимается арифметикой, знают куда больше квадратов. С кубами все обстоит сложнее, поэтому если вам требуется посчитать сумму двух кубов, куда проще использовать формулу разложения на множители. Например, давайте посчитаем выражение:

153 + 123

Сходу вычислить кубы этих чисел непросто, если вы не ученик математического кружка. Давайте используем формулу:

153 + 123 = (15 + 12) × (152 − 15×12 + 122)

Квадраты 12 и 15 многие помнят наизусть – это 144 и 225 соответственно. Осталось провести небольшие вычисления:

153 + 123 = 27 × (225 − 180 + 144) = 27 × 189 = 5 103

Проверим вычисления на калькуляторе. Число 15 в кубе дает 3 375, а 12 — 1 728. Суммируем их и получим 3 375 + 1 728 = 5 103. Все верно, но оперировать меньшими числами гораздо удобнее.

Мы представляем вам программу, которая считает сумму двух кубов с иллюстрацией промежуточных выкладок. Для расчета вам понадобится ввести значения в соответствующие ячейки и сделать один клик мышкой. Используя калькулятор, вы получите не только мгновенный и правильный ответ, но и весь процесс решения. Такая программа пригодится школьникам, которые хотят проверить свои выкладки, а также тем взрослым, кто хочет освежить в памяти школьный курс алгебры.

Заключение

Формулы сокращенного умножения – важная тема школьной алгебры, которая пригодится при решении громоздких выражений на любую тему. Это своеобразный фундамент, на котором строятся решения тригонометрических, показательных, логарифмических и даже интегральных и дифференциальных исчислений. Наш калькулятор может вам освоить применение формулы суммы двух кубов или освежить в памяти школьный материал.

КЕДР | Онлайн калькулятор пиломатериала

8 (906) 029-75-50

» Заказать звонок «

info@kedr. com.ru

» Скачать прайс-лист «

Приглашаем к сотрудничеству оптовых покупателей и поставщиков леса

На этой странице можно перевести кубометры (м3) доски, бруса и прочего пиломатериала в человекопонятные метрические штуки. Продажа досок, бруса и другого пиломатериала производится в кубометрах, но когда производиться расчёт строения (каркасного дома в т.ч.), то учёт возможно произвести вплоть до штучного количества, зная размеры бруса, так как используется в строительстве различный брус и доска, то для того что бы каждый раз не просчитывать на калькуляторе объём определённого количества досок или бруса и предназначен наш строительный калькулятор перевода объёма в штуки.

Возможны преобразования в обе стороны -
На левом калькуляторе введя размеры (бруса или доски) и количество кубометров, вы узнаете количество материалов, в том количестве кубов которое вас интересует.
На правом калькуляторе введя размеры (бруса или доски) и их количество, вы получите объём этих материалов, остаётся только умножить на цену в прайсе.
Вот так можно быстро перевести количество м3 в штуки .

Обратите внимание, что указывать размеры нужно в миллиметрах, не целые числа разделяются точкой. Например: 10мм это 1см или 0.01м

Калькулятор перевод объем пиломатериалов доски, бруса в штуки

Посчитать количество бруса (досок) в объёме м3:

Считать
Сбросить

Итого материала: 0 шт.

Пересчитать количество в объём бруса (досок):

Считать
Сбросить

Итого кубов: 0 м3.

Калькулятор перевода квадратных метров в кубические (M2->M3):

Считать
Сбросить

Итого кубов: 0 м3.

Калькулятор перевода кубических метров в квадратные (M3->M2):

Считать
Сбросить

Итого кубов: 0 м3.

Сколько метров в кубе посчитать онлайн калькулятор

Очень часто нужно быстро рассчитать количество необходимых пиломатериалов. Формулы расчета просты, но не всегда под рукой есть калькулятор. Наш онлайн-калькулятор призван помочь решить эту проблему. Вопросы о том, сколько метров в кубе и другие подобные им  решаются путем перетаскивания ползунков нижеприведенной формы.  Приведенная форма помогает легко рассчитать количество досок в 1 м.кв. зная их ширину и длину.  А если добавить толщину доски, то легко можно вычислить такие величины, как количество квадратных метров или досок в 1 м.куб.  Просто перетаскивайте ползунки и нажимайте кнопку «Посчитать».

Онлайн-калькулятор расчета количества пиломатериалов

Некоторые результаты расчета для самопроверки приводим в следующих таблицах.

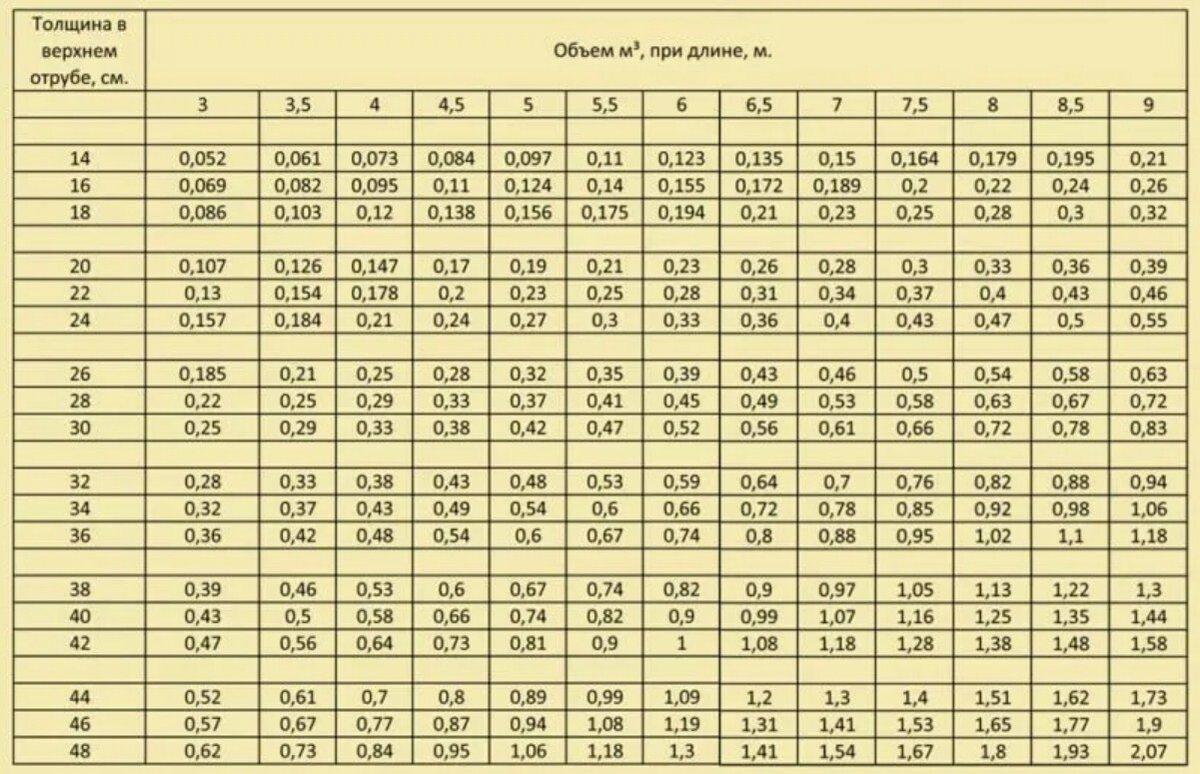
 Расчет количества доски в 1 м.куб.

толщина, ммширина, ммдлина, мкол-во, штм.кв.м.кубшт в м.кв.шт в м.куб.кв.м. в кубе
181001,510,150,0036,67370,3755,56
201202,010,240,0054,17208,3350,00
201403,010,420,0082,38119,0550,00
35703,010,210,0074,76136,0528,57
40703,010,210,0084,76119,0525,00
271204,010,480,0132,0877,1637,04
351406,010,840,0291,1934,0128,57

Расчет количества бруса в 1 м.

куб.

Количество доски на забор можно рассчитать в нашем калькуляторе расчета заборной доски

Для более точного расчета количества пиломатериалов исходя из их наличия и ассортимента  лучше связаться с нашими представителями по телефонам, указанным в шапке сайта.

Рассчитать объем коробки в м3 и литрах онлайн

07.10.2019

Сколько будет стоить отправка вашего груза до места назначения? Чтобы ответить на это вопрос, нужно знать его объем в кубических метрах, т. к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.

Картонные коробки — наиболее выгодный и удобный вид упаковки для большинства товаров. Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.

Если в результате расчета оказалось, что вам требуется гофротара индивидуальных размеров, наша компания «МС-ПАК» изготовит нужный тираж на заказ.
Рассмотрим, как правильно рассчитать объем картонной коробки.

Поэтапный расчет объема картонной коробки

Для расчета нужно:


Тип:
Профиль:
Толщина (мм):

Трехслойный гофрокартон
B
3

Трехслойный гофрокартон
C
3,7

Трехслойный гофрокартон
E
1,6

Пятислойный гофрокартон
BC
7

Пятислойный гофрокартон
BE
4