Сила тока через напряжение формула: Закон Ома онлайн — формулы и калькулятор

формулы расчета мощности в проводнике

Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.

Электрический ток в проводнике

В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.

От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:

Зависимость силы тока от электрического заряда

Входящие в формулу величины:

• I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
• Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
• Время в секундах.

Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:

I = (qnv)cosαS.

Также используется интегрирование по площади поверхности и сечению проводника.

Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.

Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:                                                                                               

Сила тока участка цепи и цепи с источником тока

Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.

В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.

При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.

Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:

RC = 1/ FC.

Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.

Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:

Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.

Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.

I = I1 + I2 + I3

Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.

Видео

Оцените статью:

Ток, напряжение, сопротивление. Закон Ома.

Мы начинаем публикацию материалов новой рубрики «Основы электроники«, и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 🙂 Кроме того, мы не обойдем стороной закон Ома, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения.

Напряжение.

По определению напряжение — это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля — это скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E. Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

U = \phi_1\medspace-\medspace \phi_2

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

\phi_1\medspace-\medspace \phi_2 = Ed

И в итоге получаем формулу, связывающую напряжение и напряженность:

U = Ed

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи — это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, «напряжение в резисторе» — не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и «землей». Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию «земля» 🙂 Так вот «землей» в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения. Единицей измерения является Вольт (В). Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт, необходимо совершить работу, равную 1 Джоулю. С этим вроде бы все понятно и можно двигаться дальше 🙂

А на очереди у нас еще одно понятие, а именно ток.

Ток, сила тока в цепи.

Что же такое электрический ток?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны… Рассмотрим проводник, к которому приложено определенное напряжение:

Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

F = Ee

где e − это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂

Ток — это упорядоченное движение заряженных частиц под воздействием электрического поля.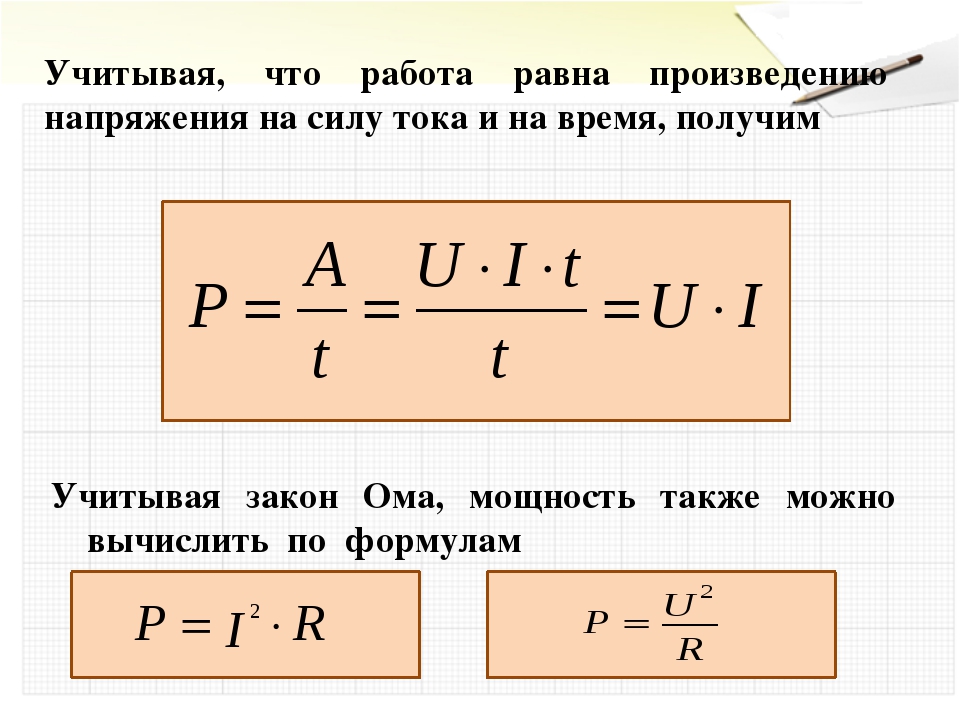

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I) — это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.

Мы уже рассмотрели понятия силы тока и напряжения, теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника.

Сопротивление проводника/цепи.

Термин «сопротивление» уже говорит сам за себя 🙂

Итак, сопротивление — физическая величина, характеризующая свойства проводника препятствовать (сопротивляться) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:

Сопротивление проводника зависит от нескольких факторов:

• удельного сопротивления проводника \rho
• длины проводника l
• площади поперечного сечения проводника S

Удельное сопротивление — это табличная величина. Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

R = \rho\medspace \frac{l}{S}

Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) — удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:

R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace Ом

Как вы уже поняли из примера, единицей измерения сопротивления является Ом 🙂

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи.

Закон Ома.

И тут на помощь нам приходит основополагающий закон всей электроники — закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

I = \frac{U}{R}

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

I = \frac{10}{200} = 0.05 = 50\medspaceмА

Как видите, все несложно 🙂 Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч!

Закон Ома.

Для цепей и тока. Формулы и применение

Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.

История

Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.

Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой.

Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.

Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.

Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.

В результате нового эксперимента Ом пришел к формуле:

Х = a / b + l

Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.

Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи.

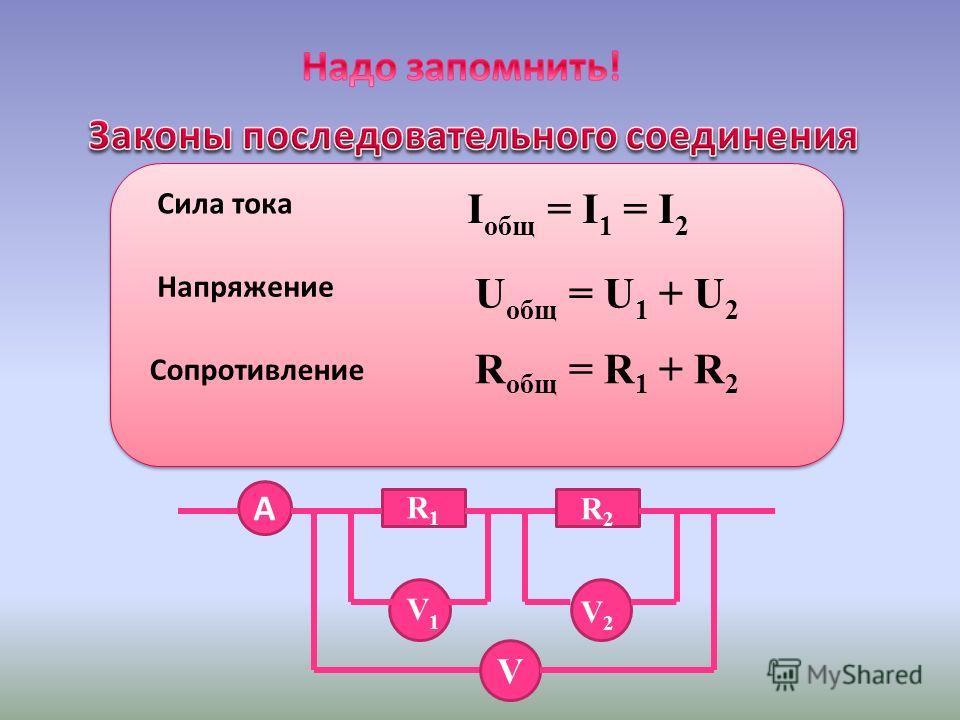
Закон Ома для участка цепи

Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.

I = U / R

Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.

Чтобы рассчитать сопротивление проводника, нужно перемножить его длину на удельное сопротивление его материала и разделить на площадь поперечного сечения.

Таким образом формула для расчета сопротивления проводника примет вид:

R = p ⋅ l / s

Закон Ома для полной цепи

Отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:

I = U / R + r

Закон Ома для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике.

Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Похожие темы:

Закон Ома — физика процесса на примере движения воды. Формулы зависимости сопротивления, напряжения, силы тока и мощности

Существует всего 2 базовых формулы которые помогут вам понять взаимосвязь между силой тока(Амер), напряжением(Вольт), сопротивлением (Ом) и мощностью (Ватт).

Зная хотя бы два из перечисленных параметра вы всегда можете рассчитать два других.

 

ЗАКОН ОМА

P — Мощность (Ватт)
E — Напряжение (Вольт)
I — Сила тока (Ампер)
R — Электрическое сопротивление (Ом)
SQR — квадратный корень

Для справки:

Мы используем переменную E для обозначения напряжения, иногда вы можете встретить  обозначение V для напряжения. Не дайте себя запутать названиям переменных.

Изменение сопротивления:

На следующей схеме вы видите разность сопротивлений между системами изображенными на правой и левой стороне рисунка. Сопротивление давлению воды в кране противодействует задвижка, в зависимости от степени открытия задвижки изменяется сопротивление.

Сопротивление в проводнике изображено в виде сужения проводника, чем более узкий проводник тем больше он противодействует прохождению тока.

Вы можете заметить что на правой и на левой стороне схемы напряжение и давление воды одинаково.

Вам необходимо обратить внимание на самый важный факт.

В зависимости от сопротивления  увеличивается и уменьшается сила тока.

Слева при полностью открытой задвижке мы видим самый большой поток воды. И при самом низком сопротивлении, видим самый большой поток электронов (Ампераж) в проводнике.

Справа задвижка закрыта намного больше и поток воды тоже стал намного больше.

ужение проводника тоже уменьшилось вдвое, я значит вдвое увеличилось сопротивление протеканию тока. Как мы видим через проводник из за выского сопротивления протекает в два раза меньше электронов.

Для справки

Обратите внимание что сужение проводника изображенное на схеме используется только для примера сопротивления протеканию тока. В реальных условиях сужения проводника не сильно влияет на протекающий ток. Значительно большее сопротивление могут оказывать полупроводники и диэлектрики.

Сужающийся проводник на схеме изображен лишь для примера, для понимания сути происходящего процесса.

Формула закона Ома — зависимость сопротивления и силы тока

I = E/R

Как вы видите из формулы, сила тока обратнапропорциональна сопротивлению цепи.

Больше сопротивление = Меньше ток

* при условии что напряжение постоянно.

 

Изменение напряжения.

На изображенной схеме во всех системах сопротивление имеет одинаковую величину.

В этот раз на картинке изменяется сопротивление/давление.

Вы можете увидеть что при увеличении напряжения приводит к увеличению протекающего тока даже при постоянном сопротивлении.

Формула закона Ома — зависимость напряжения и силы тока

I = E/R

Обратите внимание что сила тока протекающего в проводнике прямопропорциональна напряжению.

Больше напряжение = Больше сила тока

* при условии что сопротивление постоянно.

 

Математический рассчет

Рассмотрим пример.

У нас есть аккумуляторная батарея с напряжением питания 12 Вольт. К ней напрямую подключен резистор (сопротивление) 10 Ом. Для того что бы рассчитать какая мощность приложена к нашему резистору, можно воспользоваться формулой.

P = E2/R

P = 122/10

P = 144/10.
P = 14.4 watts

Мощность рассеиваемая на резисторе состовляет 14,4 Ватта.

Если вы хотите определить величину тока протекающего через проводник, мы используем другую формулу

I = E/R

I = 12/10
I = 1.2 amps

Сила тока протекающего через цепь составляет 1,2 Ампера

—————-

Калькуляторы зависимости напряжения, силы тока и сопротивления.

 

1. Калькулятор рассеиваемой мощности  и протекающей силы тока в зависимости от сопротивления и приложенного напряжения.

Демо закона Ома в реальном времени.

Для справки

В данном примере вы можете увеличивать напряжение и сопротивление цепи. Данные изменения в реальном времени будут изменять силу тока протекающего в цепи и мощность рассеиваемую на сопротивлении.

Если рассматривать аудио системы — вы должны помнить что усилитель выдает определенное напряжение на определенную нагрузку (сопротивление). Соотношение двух этих величин определяет мощность.

Усилитель может выдать ограниченную величину напряжения в зависимости от внутреннего блока питания и источника тока. Так же точно ограничена и мощность которую может подать усилитель на определенную нагрузку (к примеру 4 Ома).

Для того что бы получить больше мощности, вы можете подключить к усилителю нагрузку с меньшим сопротивлением (к примеру 2 Ома). Учтите что при использовании нагрузки с меньшим сопротивлением — скажем в два раза (было 4 Ома, стало 2 Ома) — мощность тоже возрастет в два раза.(при условии что данную мощность может обеспечить внутренний блок питания и источник тока).

Если мы возьмем для примера моно усилитель мощностью 100 Ватт на нагрузку 4 Ома, зная что он может выдать напряжение не более 20 Вольт на нагрузку.

Если вы поставите на нашем калькуляторе бегунки

Напряжение 20 Вольт

Сопротивление 4 Ома

Вы получите

Мощность 100 Ватт  

 

Если вы сдвинете бегунок сопротивления на величину 2 Ома, вы увидите как мощность удвоится и составит 200 Ватт.

В общем примере источником тока является аккумуляторная батарея (а не усилитель звука) но зависимости силы тока, напряжения, сопротивления и сопротивления одинаковы во всех цепях.

 

чему равно напряжение, как найти сопротивление нагрузки

В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.

Что такое напряжение в сети электричества.

Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.

Показатель напряжения на вольтметре

За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.

Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

Изображение вольтметра и электрической цепи

Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.

Электрическое поле

Формула закона Ома

Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.

Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.

Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению  в сети и обратно пропорционально  силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.

Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.

Ползунковый реостат

Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.

Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.

Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества.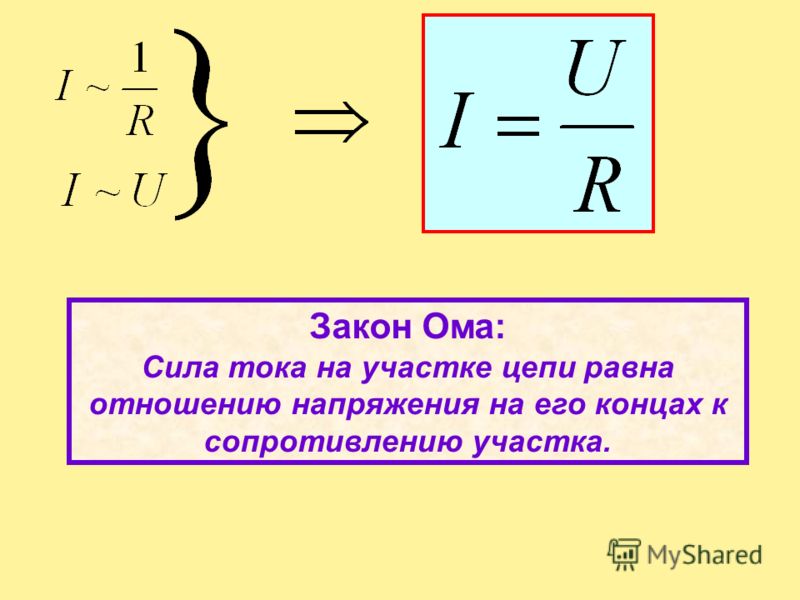 Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].

Ом и формула

Как найти сопротивление нагрузки

Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.

Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.

Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.

Последовательное/параллельное соединения

Как найти с помощью формулы напряжение

Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.

Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.

Измерение напряжения

По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми.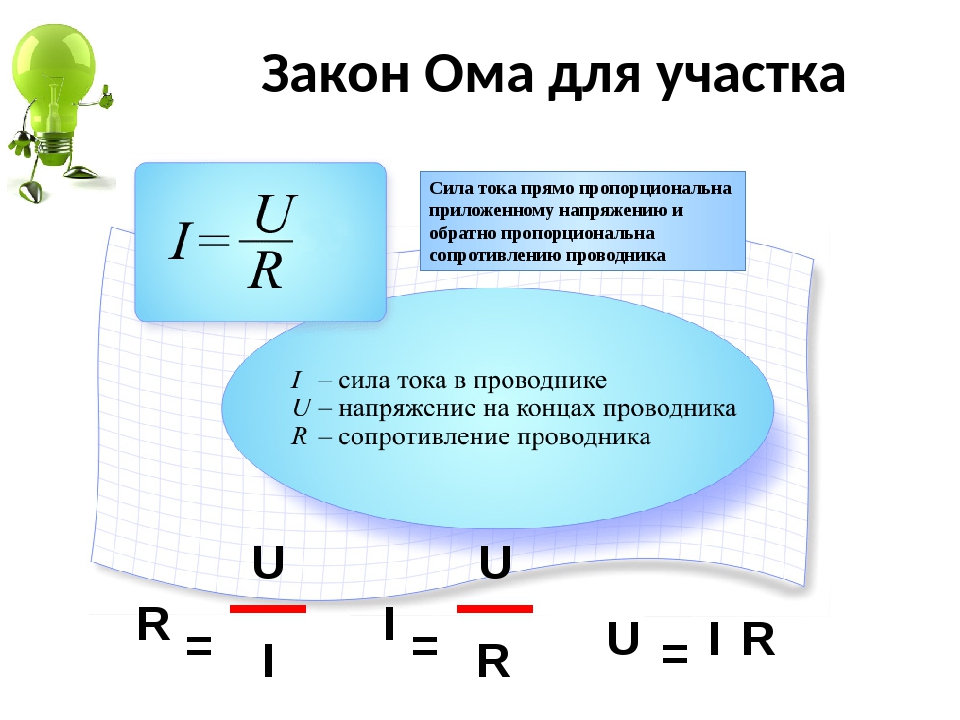 Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.

Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.

Как найти силу тока через сопротивление и напряжение

Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.

Мужчина считает силу тока

Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.

При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.

Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.

Напряжение через закон ома. Закон Ома. Для цепей и тока. Формулы и применение

Один из самых применяемых законов в электротехнике. Данный закон раскрывает связь между тремя важнейшими величинами: силой тока, напряжением и сопротивлением. Выявил эту связь Георгом Омом в 1820-е годы именно поэтому этот закон и получил такое название.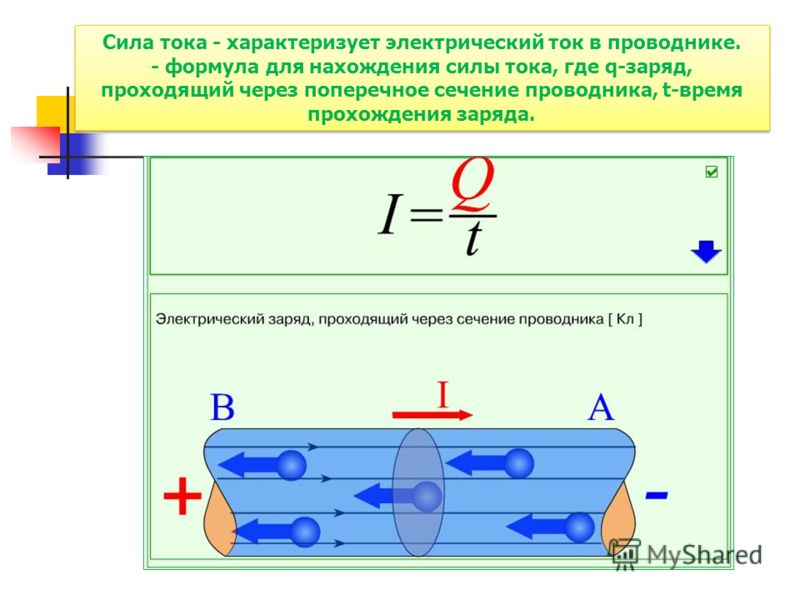

Формулировка закона Ома
следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

Где I – сила тока, U — напряжение, приложенное к участку цепи, а R — электрическое сопротивление участка цепи.
Так, если известны две из этих величин можно легко вычислить третью.
Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное). Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.
Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.
Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.
Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 — GB3 — батарейки, S1 — выключатель, HL1 — лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается. Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Что случится с лампочкой?
Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:
чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.
Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Это была обзорная статья. Более подробно об этом законе, мы говорим в следующей статье » «, рассматривая всё на других более сложных примерах.

Если не получается с физикой, английский для детей (http://www.anylang.ru/order-category/?slug=live_language) как вариент альтернативного развития.

Добавить сайт в закладки

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов:

• источника напряжения – батареи GB;
• потребителя тока – нагрузки R, которой может быть, например, нить накала электрической лампы или резистор;
• проводников, соединяющих источник напряжения с нагрузкой.

Между прочим, если эту цепь дополнить выключателем, получится полная схема карманного электрического фонаря. Нагрузка R, обладающая определенным сопротивлением, является участком цепи.

Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи.

Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:

• I – ток, выраженный в амперах, А;
• U – напряжение в вольтах, В;
• R – сопротивление в омах, Ом.

Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома) для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома:

1. Первый пример. На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи. Решение: I = U/R = 25 / 5 = 5 А.
2. Второй пример. На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
3. Третий пример. Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10 кОм = 10000 Ом). Следовательно, U = IR = 0,02×10000 = 200 В.

На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В. Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом.

Это сопротивление именно накаленной нити лампочки, сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим нужно привести еще один пример: напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000 Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.

Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы достаточно легко запомнить, если пользоваться вот этой графической схемой, это так называемый треугольник закона Ома.

Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в нем означает знак деления (по аналогии дробной черты), а вертикальная линия означает знак умножения.

Теперь следует рассмотреть такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Лучше разобрать это на примере. Имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В?

Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом.

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, то есть 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, то есть почти такой же, на который рассчитана нить накала лампочки.

Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи.

Можно включать амперметр в любую точку, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.

Добавочный резистор, включаемый в цепь последовательно с нагрузкой, можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, здесь:

• U – падение напряжения, В;
• I – ток в цепи, A;
• R – сопротивление добавочного резистора, Ом.

Применительно к примеру резистор R (см. рис.) погасил избыток напряжения: U = IR = 0,08×25 = 2 В.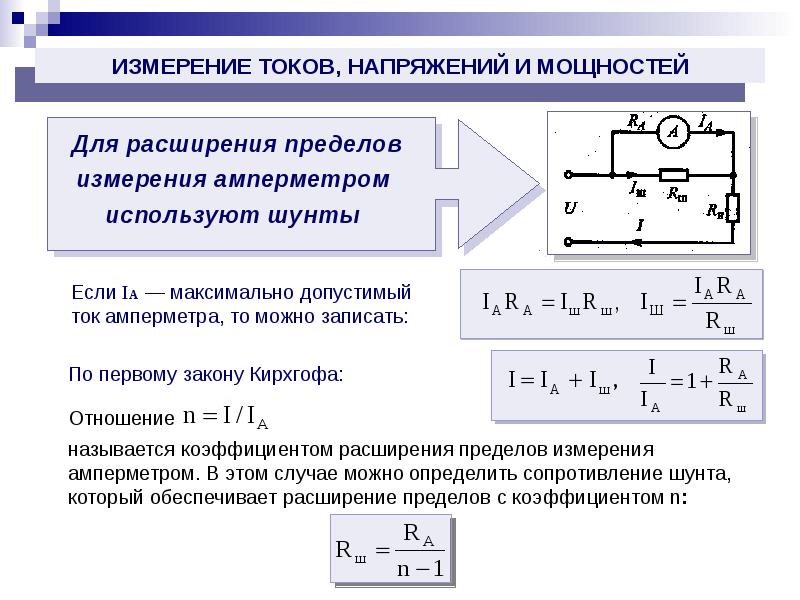 Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где:

• R – искомое сопротивление добавочного резистора, Ом;
• U – напряжение, которое необходимо погасить, В;
• I – ток в цепи, А.

Для рассматриваемого примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, таким образом регулируя ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, то есть резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом. С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть и другой способ подключения нагрузки к источнику тока с избыточным напряжением – тоже с помощью переменного резистора, но включенного потенциометром, то есть делителем напряжения, как показано на рисунке ниже.

Здесь R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания или какой-то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет).

По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение.

Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением.

Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех cлучаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком-то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой .

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных — верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет .

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила — ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Закон ома для цепи переменного тока

Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.

Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.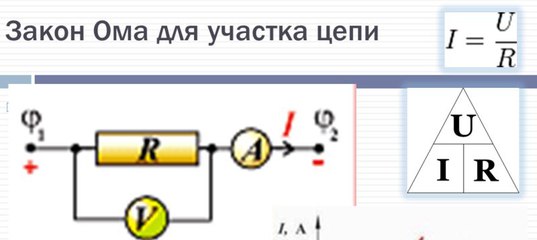

Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.

Электрическая цепь

Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.

Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока
, а силы — сторонними силами
.

Электрическую цепь, в которой находится источник тока, называют полной электрической цепью
.
Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.

Параметры электрической цепи

Свой знаменитый закон Ом вывел экспериментальным путём.

Проведём несложный опыт.

Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с
помощью ключа электрическую цепь и запишем показания приборов.

Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.

Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.

Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника
.

В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению
.

Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.

Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».

Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.

Георг Симон Ом

Закон Ома для полной цепи

Между тем, формула, выведенная самим Омом, выглядела так:

Это не что иное, как формула закона Ома для полной электрической цепи: «
Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника
».

В опытах Ома величина Х


показывала изменение величины тока. В современной формуле ей соответствует сила тока
I

, протекающего в цепи. Величина а


характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε


. Значение величины
l

зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи
R

. Параметр
b

характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это
r

– внутреннее сопротивление источника тока.

Как выводится современная формула закона Ома для полной цепи?

ЭДС источника равна сумме падений напряжений на внешней цепи (U

)
и на самом источнике (U

1

).

ε

= U

+

U

1

.

Из закона Ома
I

=

U

/

R

следует, что
U

=

I

·

R

, а
U

1

=

I

·

r

.

Подставив эти выражения в предыдущее, получим:

ε

= I · R + I · r = I · (R + r)

,
откуда

По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R
.

Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r


.

Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1


и уменьшается U


.

Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.

Короткое замыкание

А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием
. Ток, называемый током короткого замыкания
, будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.

Закон Ома для переменного тока

В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).

Для таких цепей
U

=

I

·

Z

, где
Z

— полное сопротивление, включающее в себя активную и реактивную составляющие.

Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:

I

=

U

/

R

Мощность и закон Ома

Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:

P

=

U

·

I

=

I

2

·

R

Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника. И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.

Вместо эпилога

Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.

Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома — так, как показано на рисунке.

Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.

Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Урок 3. Три друга, один треугольник и много законов

Незнание закона не освобождает от ответственности.
Афоризм

Интересно, о каких законах пойдет речь в уроке под номером три. Неужели в электротехнике этих законов целая гора или даже куча и их все нужно запомнить? Сейчас узнаем. Здравствуйте, уважаемые! Наверное, многие из вас уже с досадой в глазах глядят на очередной урок и думают про себя: «Какая же скукотища!», а, может, даже собираются покинуть наши стройные ряды? Не спешите, всё только начинается! Начальный этап всегда скучный… С этого урока и пойдёт всё самое-самое интересное. Сегодня я расскажу, кто в электротехнике кому друг, а кому и враг, что будет, если студента-электронщика разбудить посреди ночи, и как с помощью одного пальца понять половину всей электротехники. Интересно? Тогда поехали!

С первым нашим другом мы познакомились на прошлом уроке – это сила тока. Она характеризует электричество с точки зрения скорости переноса заряда из одной точки пространства в другую под действием поля. Но, как было замечено, сила тока зависит и от свойств проводника, по которому этот ток «бежит». На силу тока прямо влияет величина удельной электропроводности материала. Теперь представим себе некий проводник (подойдёт такой, как на рисунке 3) с движущимися в нём электронами. Основным недостатком электрона я бы назвал отсутствие у него руля. Из-за этого недостатка движение электронов определяется только воздействующим на них полем и структуры материала, в котором они движутся.

Поскольку электроны «не умеют» поворачивать, некоторые из них могут столкнуться с колеблющимися под действием температуры узлами кристаллической решётки, потерять свою скорость от столкновения, и тем самым снизить скорость переноса заряда, то есть понизить силу тока. Некоторые электроны могут потерять так много энергии, что «прилипнут» к иону и превратят его в нейтральный атом. Теперь, если мы увеличим длину проводника, очевидно, что количество подобных столкновений так же увеличится, и электроны будут отдавать еще больше энергии, то есть сила тока будет снижаться. А вот при увеличении площади поперечного сечения проводника возрастает только количество свободных электронов, а количество столкновений на единицу площади практически не меняется, поэтому с ростом площади растёт и ток. Итак, мы выяснили, что электропроводность (она уже стала не удельной, так как учитывает геометрические размеры конкретного проводника) зависит сразу от трёх характеристик проводника: длины, площади сечения и материала.

Однако, чем лучше материал проводит электрический ток, тем меньше он «сопротивляется» его прохождению. Эти утверждения равнозначны. Пришло время познакомиться с нашим вторым другом – электрическим сопротивлением. Это величина, обратная величине проводимости и зависит от тех же характеристик проводника.

Рисунок 3.1 – От чего зависит сопротивление проводника

Чтобы учесть при численном расчете влияние рода вещества на его электрическое сопротивление, введена величина удельное электрическое сопротивление, характеризующая способность вещества проводить электрический ток. Заметим, что определения электропроводности и электросопротивления идентичны, так же как и утверждения выше. Удельное сопротивление определяется как сопротивление проводника длиной 1м и площадью сечения 1м². Обозначается латинской буквой &#961 («ро») и имеет размерность Ом•м. Ом – единица измерения сопротивления, которая является обратной величине сименс. Так же для определения удельного сопротивления может использоваться размерность Ом•мм²/м, которая в миллион раз меньше основной размерности.
Таким образом, электрическое сопротивление проводника может быть описано через его геометрические и физические свойства следующим образом:

где &#961 – удельное электрическое сопротивление материала проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.

Из зависимости видно, что сопротивление проводника возрастает при увеличении длины проводника и уменьшается при увеличении площади сечения, а так же напрямую зависит от величины удельного сопротивления материала.

А теперь вспомним, что на величину силы тока в проводнике оказывает влияние напряженность электрического поля, под действием которого возникает электрический ток. Ох, сколько миллионов тысяч раз уже упоминалось, что электрический ток возникает под действием электрического поля! Этот факт должен всегда держаться в голове. Есть, конечно, и другие способы создать ток, но пока мы будем рассматривать только этот. Как уже говорилось выше, увеличение напряженности поля приводит к росту тока, а совсем недавно мы выяснили, что чем больше энергии сохранит электрон при движении по проводнику, тем выше значение электрического тока. Из курса механики известно, что энергия тела определяется его кинетической и потенциальной энергией. Так вот, помещённый в электрическое поле точечный заряд обладает в начальный момент времени только потенциальной энергией (поскольку его скорость равна нулю). Для характеристики этой потенциальной энергии поля, которой обладает заряд была введена величина электростатического потенциала, равная отношению потенциальной энергии к величине точечного заряда:

где W_p – потенциальная энергия,
q – величина точечного заряда.

После того, как заряд попадёт под действие электрического поля, он начнёт движение с определённой скоростью и часть его потенциальной энергии перейдёт в кинетическую. Таким образом, в двух точках поля заряд будет обладать различным значением потенциальной энергии, то есть две точки поля можно охарактеризовать различными значениями потенциала. Разность потенциалов определяется как отношение изменения потенциальной энергии (совершённой работы поля) к величине точечного заряда:

Причём работа поля не зависит от пути движения заряда и характеризует только величину изменения потенциальной энергии. Разность потенциалов так же называют электрическим напряжением. Напряжение принято обозначать английской буквой U («у»), единицей измерения напряжения является величина вольт (В), названная в честь итальянского физика и физиолога Алессандро Вольта, который изобрёл первую электрическую батарею.

Ну вот мы и познакомились с тремя неразлучными друзьями в электротехнике: ампер, вольт и ом или ток, напряжение и сопротивление. Любой компонент электрической цепи может быть однозначно охарактеризован при помощи этих трёх электрических характеристик. Первым, кто познакомился и подружился со всеми тремя сразу был Георг Ом, который обнаружил, что напряжение, ток и сопротивление связаны друг с другом определённым соотношением:

которое было впоследствии названо законом Ома.

Сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника.

Данную формулировку необходимо знать от заглавной буквы С до точки в конце. Ходят слухи, что первая фраза любого студент-электронщик, разбуженного среди ночи, будет именно формулировкой закона Ома. Это один из основных законов электротехники. Данная формулировка носит название интегральной. Кроме неё существует так же дифференциальная формулировка, отражающая зависимость плотности тока от характеристик поля и материала проводника:

где &#963 – удельная проводимость проводника,
E – напряженность электрического поля.

Данная формулировка вытекает из формулы, приведённой во втором уроке, и отличается от интегральной тем, что не учитывает геометрические характеристики проводника, принимая во внимание только его физические характеристики. Эта формулировка интересна только с точки зрения теории и на практике не применяется.
Для быстрого запоминания и использования закона Ома можно применить диаграмму, изображённую на рисунке ниже.

Рисунок 3.2 – «Треугольный» закон Ома

Правило использования диаграммы простое: достаточно закрыть искомую величину и два других символа дадут формулу для её вычисления. Например.

Рисунок 3.3 – Как запомнить закон Ома

С треугольником мы закончили. Стоит добавить, что законом Ома называется только одна из представленных выше формул – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют. Так что не перепутайте!
Хорошей интерпретацией закона Ома является рисунок, который наиболее наглядно отражает сущность этого закона:

Рисунок 3.4 – Закон Ома наглядно

Как мы видим, на этом рисунке изображены как раз три наших новых друга: Ом, Ампер и Вольт. Вольт пытается протолкнуть Ампер через сечение проводника(сила тока прямо пропорциональна напряжению), а Ом наоборот – мешает этому (и обратно пропорциональна сопротивлению). И чем сильнее Ом «стягивает» проводник, тем тяжелее Амперу будет пролезть. Но если Вольт посильнее пнёт…

Осталось разобраться, почему в названии урока фигурирует термин «много законов», ведь закон-то у нас один – закон Ома. Ну, во-первых, для него существует две формулировки, во-вторых, мы узнали только так называемый закон Ома для участка цепи, а ведь есть ещё закон Ома для полной цепи, который мы рассмотрим на следующем уроке, в-третьих, мы имеем, по крайней мере, два следствия из закона Ома, позволяющих находить значение сопротивления участка цепи и напряжение на этом участке. Так что закон всего один, а использовать его можно по-разному.

Напоследок расскажу ещё один интересный факт. Через 10 лет после появления «закона Ома» один французский физик (а во Франции работы Ома ещё не были известны) на основе экспериментов пришел к таким же выводам. Но ему было указано, что установленный им закон еще в 1827г. был открыт Омом. Оказывается, что французские школьники и поныне изучают закон Ома под другим именем – для них это закон Пулье. Вот так вот. На этом очередной урок закончен. До новых встреч!

• Любой участок или элемент электрической цепи можно однозначно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
• Сопротивление (R) – характеристика проводника, отражающая степень его электропроводности и зависящая от геометрических размеров проводника и рода материала, из которого он изготовлен.
• Напряжение (U) – то же самое, что и разность потенциалов; величина равная отношению работы электрического поля для перемещения точечного заряда из одной точки пространства в другую.
• Ток, напряжение и сопротивление связаны между собой отношением I=U/R, называемым законом Ома (сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника).

А также задачки:

• Если длину проволоки вытягиванием увеличить вдвое, то как изменится её сопротивление?
• Какой проводник представляет большее сопротивление: медный сплошной стержень или медная трубка, имеющая внешний диаметр, равный диаметру стержня?
• Разность потенциалов на концах алюминиевого проводника равна 10В. Определить плотность тока, протекающего через проводник, если его длина 3м.

← Урок 2: Как пересчитать электроны | Содержание | Урок 4: Когда есть ток? →

Ток, сопротивление, напряжение и мощность

Текущий

Ток — это мера потока электрического заряда через материал. Материал, который может переносить поток заряда, называется проводником. Ток определяется как количество заряда, которое проходит через проводник за определенное время. Единицей измерения тока является ампер (A), который равен одному кулону в секунду (кулон — единица заряда),

Символ I используется для обозначения тока (хотя J часто используется в инженерные источники).Ток I через проводник зависит от его площади A , концентрации n носителей заряда, величины заряда q каждого носителя и величины их средней (или «дрейфующей») скорости. v _d ,

Плотность тока — это количество тока, протекающего через проводник, деленное на его площадь,

Направление потока определяется в терминах потока положительных зарядов (даже если фактические носители заряда отрицательны).Единица измерения плотности тока — Амперы на квадратный метр (А / м ² ).

Удельное сопротивление
Некоторые проводники переносят заряд легче, чем другие. Удельное сопротивление материала описывает, насколько легко может течь заряд. Хорошие проводники имеют небольшое удельное сопротивление, а хорошие изоляторы — большое. Удельное сопротивление ρ (греческая буква «ро») равно величине электрического поля в материале, деленной на плотность тока,

Единицей измерения величины электрического поля является вольт на метр (В / м). ), а единицей измерения плотности тока является Ампер на квадратный метр (А / м ² ), поэтому единицей измерения удельного сопротивления является Вольт-метр на Ампер,

Многие проводники подчиняются закону Ома.Материалы, которые подчиняются закону Ома, имеют постоянное удельное сопротивление независимо от значений электрического поля E и плотности тока J. Формулы, относящиеся к цепям, верны для «омических» материалов, а «неомические» материалы в этом курсе не обсуждаются.

Удельное сопротивление омического проводника зависит от температуры материала. Зависящее от температуры удельное сопротивление ρ (T) можно найти по формуле:

Эта формула требует ρ ₀ , удельного сопротивления при эталонной температуре T ₀ .Температурный коэффициент удельного сопротивления α различен для каждого материала. Для температур в градусах Цельсия (℃) температурный коэффициент удельного сопротивления имеет единицы: 1 / ℃ = (℃) ^(-1)

Сопротивление
Удельное сопротивление — это свойство материала, а сопротивление — это свойство определенного куска этого материала. Сопротивление отрезка проводника зависит от его длины L, площади A и удельного сопротивления ρ,

Единицей измерения сопротивления является Ом, который обозначается греческой буквой Ω («омега»).Один Ом равен одному Вольту на Ампер,

Сопротивление зависит от температуры так же, как и удельное сопротивление,

Для этой формулы требуется R ₀ , сопротивление при эталонной температуре T ₀ . Температурный коэффициент α отличается для каждого материала, как описано в разделе Сопротивление .

Резистор — это устройство, которое используется в электрических цепях и имеет определенное фиксированное сопротивление. Резисторы изготавливаются путем выбора куска материала с определенным удельным сопротивлением, длиной и площадью и обертывания его изолятором с проводами, выходящими из каждого конца.На принципиальных схемах он представлен символом

Напряжение
Напряжение — это разница в электрическом потенциале между двумя точками. Если электрическое поле однородно через проводник, разность потенциалов будет равна,

Используя уравнения в Ток, Удельное сопротивление, и
Сопротивление секций, можно найти другое уравнение для разности потенциалов,

Уравнение V = IR означает, что разность потенциалов или напряжение на резисторе можно найти, умножив его сопротивление на ток, протекающий через него.Единицей измерения разности потенциалов является вольт (В), который равен джоуля на кулон (Дж / Кл).

Источник напряжения — это устройство, используемое в электрических цепях, которое имеет фиксированную разность потенциалов между его концами. Источником напряжения может быть батарея или другой источник постоянного тока с фиксированной разностью потенциалов. На принципиальных схемах он представлен символом

Если концы источника напряжения соединены через цепь с любым количеством резисторов или других компонентов, образуется полная цепь, и ток может течь от одного вывода к другому. другой.Если ток течет, он будет одинаковым на обоих выводах источника напряжения.

Источник напряжения, который является частью полной схемы, может создавать электродвижущую силу, которая обозначается символом ε («скрипт e»). Единицей электродвижущей силы является вольт (В), который равен джоуля на кулон (Дж / Кл). Для идеального источника электродвижущая сила равна разнице напряжений,

Настоящие источники, такие как батареи, не идеальны, поэтому существует некоторое внутреннее сопротивление.Если внутреннее сопротивление батареи равно r, то разница напряжений на батарее равна

Это также называется напряжением на клеммах батареи. Если полная цепь сделана с использованием резистора с сопротивлением R, ток, протекающий через цепь, можно найти с помощью уравнения V = IR,

Ток равен электродвижущему. сила источника, деленная на полное сопротивление цепи.

Мощность

Мощность (P) — это мера скорости, с которой энергия передается или используется элементом схемы. Источники напряжения обеспечивают питание, а резисторы используют мощность (рассеивая ее в виде тепла). Мощность равна напряжению на элементе схемы, умноженному на ток, протекающий через него,

Единицей измерения мощности является ватт (Вт), который равен джоулям в секунду,

Это соотношение может быть определяется по формуле для мощности:

Мощность, потребляемая или рассеиваемая резистором, может быть найдена по формуле V = IR.Эта формула может использоваться для замены напряжения или тока в формуле мощности,

,

и

Выходная мощность батареи с внутренним сопротивлением может быть найдена по формуле V = ε-Ir и формула мощности,

10.6: RC Circuits — Physics LibreTexts

При использовании камеры со вспышкой для зарядки конденсатора, питающего вспышку, требуется несколько секунд.Световая вспышка разряжает конденсатор за крошечные доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и несколько других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.

Цепи сопротивления и емкости

Цепь RC — это цепь, содержащая сопротивление и емкость. Как показано в разделе «Емкость», конденсатор — это электрический компонент, который накапливает электрический заряд, накапливая энергию в электрическом поле.

На рисунке \ (\ PageIndex {1a} \) показана простая схема RC , в которой используется источник постоянного напряжения \ (ε \), резистор \ (R \), конденсатор \ (C \), и двухпозиционный переключатель. Схема позволяет конденсатору заряжаться или разряжаться в зависимости от положения переключателя. Когда переключатель перемещается в положение \ ( A \) , конденсатор заряжается, в результате получается схема, показанная на рисунке \ (\ PageIndex {1b} \). Когда переключатель перемещается в положение B , конденсатор разряжается через резистор.

Рисунок \ (\ PageIndex {1} \): (a) Схема RC с двухполюсным переключателем, который можно использовать для зарядки и разрядки конденсатора. (b) Когда переключатель перемещается в положение A , схема сводится к простому последовательному соединению источника напряжения, резистора, конденсатора и переключателя. (c) Когда переключатель перемещается в положение B , схема сводится к простому последовательному соединению резистора, конденсатора и переключателя. Источник напряжения снят с цепи.

Зарядка конденсатора

Мы можем использовать правило петли Кирхгофа, чтобы понять заряд конденсатора. Это приводит к уравнению \ (\ epsilon — V_R — V_C = 0 \). Это уравнение можно использовать для моделирования заряда как функции времени при зарядке конденсатора. Емкость определяется как \ (C = q / V \), поэтому напряжение на конденсаторе равно \ (V_C = \ frac {q} {C} \). Согласно закону Ома падение потенциала на резисторе равно \ (V_R = IR \), а ток определяется как \ (I = dq / dt \). {- t / \ tau } \).{-t / \ tau}) \).

Разряд конденсатора

Когда переключатель на рисунке \ (\ PageIndex {3a} \) перемещается в положение B , схема сокращается до схемы в части (c), и заряженному конденсатору позволяют разрядиться через резистор. График зависимости заряда конденсатора от времени показан на рисунке \ (\ PageIndex {3a} \). Использование правила петли Кирхгофа для анализа цепи при разряде конденсатора приводит к уравнению \ (- V_R -V_C = 0 \), которое упрощается до \ (IR + \ frac {q} {C} = 0 \).{-t / \ tau}. \]

Отрицательный знак показывает, что ток течет в направлении, противоположном току, наблюдаемому при зарядке конденсатора. На рисунке \ (\ PageIndex {3b} \) показан пример графика зависимости заряда от времени и тока от времени. График зависимости разности напряжений на конденсаторе и разницы напряжений на резисторе от времени показан на рисунках \ (\ PageIndex {3c} \) и \ (\ PageIndex {3d} \). Обратите внимание, что величины заряда, тока и напряжения экспоненциально уменьшаются, приближаясь к нулю с увеличением времени.

Рисунок \ (\ PageIndex {3} \): (a) Заряд конденсатора в зависимости от времени, когда конденсатор разряжается. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.

Теперь мы можем объяснить, почему вспышка камеры , упомянутая в начале этого раздела, требует гораздо больше времени для зарядки, чем для разрядки: сопротивление во время зарядки значительно больше, чем во время разрядки. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки.По мере старения аккумулятора возрастающее внутреннее сопротивление делает процесс зарядки еще медленнее.

Пример \ (\ PageIndex {2} \): Осциллятор релаксации

Одним из применений схемы RC является релаксационный генератор, как показано ниже. Релаксационный генератор состоит из источника напряжения, резистора, конденсатора и неоновой лампы. Неоновая лампа действует как разомкнутая цепь (бесконечное сопротивление), пока разность потенциалов на неоновой лампе не достигнет определенного напряжения.При таком напряжении лампа действует как короткое замыкание (нулевое сопротивление), и конденсатор разряжается через неоновую лампу и производит свет. В показанном релаксационном генераторе источник напряжения заряжает конденсатор до тех пор, пока напряжение на конденсаторе не станет 80 В. Когда это происходит, неон в лампе выходит из строя и позволяет конденсатору разряжаться через лампу, создавая яркую вспышку. После того, как конденсатор полностью разрядится через неоновую лампу, он снова начинает заряжаться, и процесс повторяется.{-t / \ tau}) = ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right), \]

\ [t = — \ tau ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right) = -5.05 \, s \ cdot ln \ left (1 — \ frac {80 \, V } {100 \, V} \ right) = 8.13 \, s. \]

Значение

Одним из применений генератора релаксации является управление световыми индикаторами, которые мигают с частотой, определяемой значениями для R и C . В этом примере неоновая лампа будет мигать каждые 8,13 секунды с частотой \ (f = \ frac {1} {T} = \ frac {1} {8.13 \, s} = 0,55 \, Гц \). Осциллятор релаксации имеет много других практических применений. Он часто используется в электронных схемах, где неоновая лампа заменяется транзистором или устройством, известным как туннельный диод. Описание транзистора и туннельного диода выходит за рамки этой главы, но вы можете рассматривать их как переключатели, управляемые напряжением. Обычно это разомкнутые переключатели, но при подаче правильного напряжения переключатель замыкается и проводит ток. «Выключатель» можно использовать для включения другой цепи, включения света или запуска небольшого двигателя.Осциллятор релаксации может быть использован для того, чтобы заставить мигать поворотники вашего автомобиля или ваш мобильный телефон вибрировать.

Цепи RC имеют множество применений. Их можно эффективно использовать в качестве таймеров для таких приложений, как стеклоочистители прерывистого действия, кардиостимуляторы и стробоскопы. В некоторых моделях стеклоочистителей прерывистого действия используется переменный резистор для регулировки интервала между движениями стеклоочистителя. Увеличение сопротивления увеличивает постоянную времени RC , что увеличивает время между срабатываниями дворников.

Еще одно приложение — кардиостимулятор . Частота сердечных сокращений обычно контролируется электрическими сигналами, которые заставляют сердечные мышцы сокращаться и перекачивать кровь. Когда сердечный ритм ненормален (сердцебиение слишком высокое или слишком низкое), для исправления этого нарушения можно использовать кардиостимуляторы. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время физических нагрузок, таким образом удовлетворяя повышенную потребность в крови и кислороде, а схема синхронизации RC может использоваться для управления временем между сигналами напряжения, подаваемыми на сердце.

Забегая вперед к изучению цепей переменного тока (цепей переменного тока), напряжения переменного тока изменяются как синусоидальные функции с определенными частотами. Ученые часто регистрируют периодические изменения напряжения или электрических сигналов. Эти сигналы напряжения могут исходить от музыки, записанной с помощью микрофона, или от атмосферных данных, собранных радаром. Иногда эти сигналы могут содержать нежелательные частоты, известные как «шум». RC фильтры могут использоваться для фильтрации нежелательных частот.

В области изучения электроники популярное устройство, известное как таймер 555, выдает синхронизированные импульсы напряжения. Время между импульсами контролируется схемой RC . Это лишь некоторые из бесчисленных применений схем RC .

Пример \ (\ PageIndex {2} \): прерывистые работы дворников

Осциллятор релаксации используется для управления парой дворников. Релаксационный генератор состоит из конденсатора емкостью 10,00 мФ и переменного резистора (10,00 кОм), известного как реостат.Ручка, подключенная к переменному резистору, позволяет регулировать сопротивление от \ (0.00 \, \ Omega \) до \ (10.00 \, k \ Omega \). Выход конденсатора используется для управления переключателем, управляемым напряжением. Переключатель обычно разомкнут, но когда выходное напряжение достигает 10,00 В, переключатель замыкается, запитывая электродвигатель и разряжая конденсатор. Двигатель заставляет дворники один раз подметать лобовое стекло, и конденсатор снова начинает заряжаться. На какое сопротивление нужно регулировать реостат при периоде работы щеток стеклоочистителя 10.3 \, \ Omega) ln \ left (1 — \ frac {10 \, V} {12 \, V} \ right) = 179,18 \, s = 2,98 \, мин. \]

Схема RC имеет тысячи применений и очень важна для изучения. Его можно не только использовать для измерения времени в цепях, но и для фильтрации нежелательных частот в цепи и использовать в источниках питания, например, в вашем компьютере, чтобы преобразовать переменное напряжение в постоянное.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Как соотносятся напряжение, ток и сопротивление: Закон Ома

Том I — Округ Колумбия »ЗАКОН ОМА»

Электрическая цепь образуется, когда создается токопроводящий путь для
позволяют свободным электронам непрерывно двигаться. Это непрерывное движение
Свободные электроны, проходящие через проводники цепи, называют током , и его часто называют «потоком», как поток жидкости через полую трубу.

Сила, побуждающая электроны «течь» в цепи, называется напряжением , напряжением .
Напряжение — это особая мера потенциальной энергии, которая всегда
относительный между двумя точками. Когда мы говорим об определенном количестве
напряжение, присутствующее в цепи, мы имеем в виду измерение
о том, сколько потенциальной энергии существует для перемещения электронов из одной конкретной точки в этой цепи в другую конкретную точку. Без ссылки на две конкретные точки термин «напряжение» не имеет значения.

Свободные электроны имеют тенденцию перемещаться по проводникам с некоторой степенью
трение или противодействие движению. Это противодействие движению больше
правильно называется сопротивление . Количество тока
в цепи зависит от количества доступного напряжения, чтобы мотивировать
электронов, а также количество сопротивления в цепи, чтобы противостоять
электронный поток. Как и напряжение, сопротивление — величина относительная.
между двумя точками. По этой причине величины напряжения и
сопротивление часто указывается как «между» или «поперек» двух точек
в цепи.

Чтобы иметь возможность делать значимые заявления об этих количествах в
цепей, мы должны иметь возможность описывать их количество в одном и том же
способ, которым мы могли бы количественно определить массу, температуру, объем, длину или любой другой
другой вид физической величины. Для массы мы можем использовать единицы
«фунт» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или
градусов Цельсия. Вот стандартные единицы измерения для
электрический ток, напряжение и сопротивление:

«Символ», указанный для каждого количества, является стандартным буквенным обозначением.
буква, используемая для обозначения этой величины в алгебраическом уравнении.Подобные стандартизированные буквы распространены в дисциплинах
физика и техника, и признаны во всем мире. Единица
аббревиатура «для каждого количества представляет собой используемый алфавитный символ.
как сокращенное обозначение его конкретной единицы измерения. А также,
да, этот странный на вид символ «подкова» — заглавная греческая
буква Ω, просто символ в иностранном алфавите (извинения перед читателями-греками).

Каждая единица измерения названа в честь известного экспериментатора в области электричества: amp в честь француза Андре М.Ампер, вольт после итальянского Алессандро Вольта и Ом после немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. В
«R» для сопротивления и «V» для напряжения говорят сами за себя,
тогда как «I» для тока
кажется немного странным. Считается, что «я» должно было представлять
«Интенсивность» (потока электронов) и другой символ напряжения, «E».
расшифровывается как «Электродвижущая сила.»Из каких исследований мне удалось
Да, похоже, есть некоторые споры о значении «я». Символы
«E» и «V» по большей части взаимозаменяемы, хотя некоторые тексты
зарезервируйте «E» для обозначения напряжения на источнике (таком как батарея или
генератор) и «V» для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток)
описывается в терминах короткого периода времени (называемого
«мгновенное» значение).Например, напряжение батареи, которое
стабильный в течение длительного периода времени, будет обозначаться заглавной буквой
буква «Е», а пик напряжения удара молнии в самом
момент, когда он попадет в линию электропередачи, скорее всего, будет обозначен
строчная буква «е» (или строчная буква «v») для обозначения этого значения как
находясь в один момент времени. Это же соглашение о нижнем регистре выполняется
верно и для тока, строчная буква «i» обозначает ток в некоторый момент времени.Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.

Одна основополагающая единица электрического измерения, которой часто учат в
начало курсов электроники, но впоследствии редко используемое,
блок кулон ,
который является мерой электрического заряда, пропорциональной количеству
электроны в несбалансированном состоянии. Один кулон заряда равен
6 250 000 000 000 000 000 электронов.Символ электрического заряда
количество — заглавная буква «Q» с единицей измерения кулоны.
сокращенно заглавной буквой «C». Так получилось, что агрегат для
поток электронов, amp, равен 1 кулону электронов, проходящих через
заданная точка в цепи за 1 секунду времени. В этих терминах ток — это скорость движения электрического заряда по проводнику.

Как указывалось ранее, напряжение — это мера потенциальной энергии на единицу заряда , доступной для перемещения электронов из одной точки в другую.Прежде чем мы сможем точно определить, что такое «вольт»
то есть, мы должны понять, как измерить эту величину, которую мы называем «потенциал
энергия ». Общая единица измерения энергии любого вида — джоуль ,
равно количеству работы, выполненной приложенной силой в 1 ньютон
через движение на 1 метр (в том же направлении). В британских частях
это чуть меньше 3/4 фунта силы, приложенной на расстоянии
1 фут. Проще говоря, требуется около 1 джоуля энергии для
поднимите гирю 3/4 фунта на 1 фут от земли или перетащите что-нибудь
расстояние в 1 фут с использованием параллельного тягового усилия 3/4 фунта.Определенный
в этих научных терминах 1 вольт равен 1 джоуля электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, батарея на 9 вольт выделяет 9 джоулей энергии на каждый кулон электронов, перемещаемых по цепи.

Эти единицы и символы электрических величин станут очень
важно знать, когда мы начинаем исследовать отношения между ними
в схемах. Первые и, пожалуй, самые важные отношения
между током, напряжением и сопротивлением называется законом Ома, открытым Георгом Саймоном Омом и опубликованным в его статье 1827 года Математические исследования гальванической цепи .Главное открытие Ома заключалось в том, что величина электрического тока
через металлический проводник в цепи прямо пропорционально
напряжение, приложенное к нему, для любой заданной температуры. Ом выражен
его открытие в виде простого уравнения, описывающего, как напряжение,
ток и сопротивление взаимосвязаны:

В этом алгебраическом выражении напряжение (E) равно току
(I) умноженное на сопротивление (R). Используя методы алгебры, мы можем
преобразовать это уравнение в два варианта, решая для I и R,
соответственно:

Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:

В приведенной выше схеме есть только один источник напряжения (аккумулятор слева) и только один источник сопротивления току.
(лампа справа).Это позволяет очень легко применять закон Ома.
Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы рассчитаем величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Какая величина тока (I) в этой цепи?

В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Какое сопротивление (R) предлагает лампа?

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Какое напряжение обеспечивает аккумулятор?

Закон Ома — очень простой и полезный инструмент для анализа электрических
схемы.Он так часто используется при изучении электричества и
электроники, которую нужно сохранить в памяти серьезными
ученик. Для тех, кто еще не знаком с алгеброй, есть
трюк с запоминанием того, как решить для любого одного количества, учитывая другое
два. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

В конце концов, вам придется познакомиться с алгеброй, чтобы серьезно
изучать электричество и электронику, но этот совет может сделать ваш первый
расчеты запомнить немного легче.Если тебе комфортно с
алгебры, все, что вам нужно сделать, это зафиксировать E = IR в памяти и получить
другие две формулы из того, когда они вам понадобятся!

• ОБЗОР:
• Напряжение измеряется в вольт , обозначается буквами «E» или «V».
• Ток измеряется в амперах , обозначается буквой «I».
• Сопротивление измеряется в Ом , обозначается буквой «R».
• Закон Ома: E = IR; I = E / R; R = E / I

Закон

Ома: определение и взаимосвязь между напряжением, током и сопротивлением — Видео и стенограмма урока

Закон Ома

Взаимосвязь между напряжением, током и сопротивлением описывается законом Ома .Это уравнение, i = v / r , говорит нам, что ток, i , протекающий по цепи, прямо пропорционален напряжению, v , и обратно пропорционален сопротивлению, r . Другими словами, если мы увеличим напряжение, то увеличится и ток. Но, если увеличить сопротивление, то ток уменьшится. Мы увидели эти концепции в действии с садовым шлангом. Увеличение давления привело к увеличению потока, но изгиб шланга увеличил сопротивление, что привело к уменьшению потока.

Эта диаграмма — простой способ решать уравнения.

Как здесь написано уравнение, было бы легко использовать закон Ома, чтобы вычислить ток, если бы мы знали напряжение и сопротивление. Но что, если бы мы вместо этого захотели вычислить напряжение или сопротивление? Один из способов сделать это — переставить члены уравнения для решения других параметров, но есть более простой способ. Приведенная выше диаграмма даст нам соответствующее уравнение для решения любого неизвестного параметра без использования алгебры.Чтобы использовать эту диаграмму, мы просто закрываем параметр, который пытаемся найти, чтобы получить правильное уравнение. Это станет более понятным, когда мы начнем его использовать, поэтому давайте рассмотрим несколько примеров.

Закон Ома в действии

Ниже представлена ​​простая электрическая схема, которую мы будем использовать для выполнения наших примеров. Наш источник напряжения — это аккумулятор, подключенный к лампочке, которая обеспечивает сопротивление электрическому току. Для начала предположим, что наша батарея имеет напряжение 10 вольт, электрическая лампочка имеет сопротивление 20 Ом, и нам нужно вычислить ток, протекающий по цепи.Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, то есть ток, или i , и это оставляет нам напряжение v , превышающее сопротивление, r . Другими словами, чтобы найти ток, нам нужно разделить напряжение на сопротивление. Делая математические вычисления, 10 вольт, разделенные на 20 Ом, дают половину ампера тока, протекающего в цепи.

Чтобы найти ток, разделите напряжение (20 вольт) на сопротивление (20 Ом).

Теперь давайте увеличим напряжение, чтобы посмотреть, что происходит с током.Мы будем использовать ту же лампочку, но перейдем на 20-вольтовую батарею. Используя то же уравнение, что и раньше, мы разделим 20 вольт на 20 Ом, и мы получим 1 ампер тока. Как мы видим, удвоение напряжения привело к удвоению тока. Это имеет смысл, когда мы думаем о садовом шланге. Если бы мы увеличили давление в шланге, можно было бы ожидать, что поток воды также увеличится. Всегда полезно перепроверить свою работу, спросив, соответствуют ли результаты тому, что вы ожидали.

Если бы мы увеличили сопротивление лампочки, что бы вы ожидали, что произойдет с током? Чтобы выяснить это, давайте поменяем существующую лампочку на другую с сопротивлением 40 Ом.Поскольку мы все еще ищем ток, мы используем то же уравнение, что и раньше. Разделив 20 вольт на 40 Ом, мы получим половину ампера тока. Этот результат говорит нам, что удвоение сопротивления уменьшило ток вдвое. Вы этого ожидали? Если вернуться к нашему шлангу, логично предположить, что перегиб в шланге уменьшит поток воды, точно так же, как увеличение сопротивления в цепи уменьшит ток.

До сих пор мы только рассчитали ток в цепи, но что, если бы кто-то поменял нашу лампочку, когда мы не смотрели, и нам нужно было вычислить сопротивление новой? Что ж, мы знаем, что напряжение нашей батареи составляет 20 вольт, и мы можем измерить ток в цепи с помощью инструмента, называемого амперметром, поэтому все, что нам осталось, — это выполнить некоторые вычисления.Используя нашу диаграмму, мы скрываем параметр, который мы пытаемся найти, а именно сопротивление, r . Схема теперь показывает нам, что нам нужно разделить напряжение на ток. Если наш амперметр измерил ток в 5 ампер, протекающий по цепи, то сопротивление будет равно 20 вольт, разделенным на 5 ампер, что составляет 4 Ом

Чтобы определить напряжение, умножьте силу тока (3 ампера) на сопротивление (4 Ом).

Наконец, представьте, что кто-то заменил нашу батарею, и нам нужно выяснить ее напряжение.Процесс почти такой же. Мы знаем, что наша новая лампочка имеет сопротивление 4 Ом, и мы можем измерить ток в цепи с помощью амперметра. Используя диаграмму, мы покрываем напряжение v , которое говорит нам, что нам нужно умножить ток на сопротивление. Если бы амперметр измерил ток в 3 ампера, тогда напряжение было бы 3 ампера, умноженным на 4 Ом, что составляет 12 вольт. Это все, что нужно сделать. Зная любые два из трех параметров, мы всегда можем вычислить третий, используя закон Ома.

Краткое содержание урока

Закон Ома определяет соотношение между напряжением, током и сопротивлением в электрической цепи: i = v / r . Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Это означает, что увеличение напряжения приведет к увеличению тока, а увеличение сопротивления приведет к уменьшению тока. Зная любые два из трех параметров, мы можем вычислить третий, неизвестный параметр.Мы можем сделать это, переставив члены в уравнении закона Ома или используя диаграмму, приведенную выше в уроке. Скрытие параметра, который мы пытаемся найти, показывает нам соответствующее уравнение с использованием двух известных параметров.

Результаты обучения

По завершении этого урока вы сможете:

• Описывать взаимосвязь между напряжением, током и сопротивлением, используя закон Ома
• Напишите уравнение закона Ома
• Объясните, как можно найти любую из трех переменных в уравнении закона Ома, если вы знаете две другие
• Рассчитайте любую из трех переменных, используя уравнение закона Ома

Закон Кирхгофа для сложных схем | ОРЕЛ

Закон

Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша схема более сложная? Возможно, вы разрабатываете электронику с параллельным и последовательным сопротивлением, и закон Ома начинает падать.Или что, если у вас нет источника постоянного тока? В таких ситуациях, когда нельзя использовать только V = IR, пора встать на плечи Ома и применить закон Кирхгофа. Здесь мы рассмотрим, что такое Закон Кирхгофа для цепей и как его использовать для анализа напряжения и тока сложных электрических цепей.

Что такое Окружной закон Кирхгофа?

Когда вы строите сложную схему, включающую мосты или Т-образные сети, вы не можете полагаться исключительно на закон Ома для определения напряжения или тока.Здесь пригодится закон Кирхгофа, который позволяет рассчитывать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Существует два варианта закона Кирхгофа, в том числе:

• Закон Кирхгофа: Для анализа полного тока сложной цепи
• Закон Кирхгофа о напряжении : анализ общего напряжения для сложной цепи
• Когда вы объединяете эти два закона, вы получаете Окружной закон Кирхгофа

Как и любой другой научный или математический закон, названный в честь их создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом.Густав был известен многими достижениями при жизни, включая теорию спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент периодической таблицы имеет свою уникальную длину волны. Открытие этого паттерна позволило дуэту открыть два новых элемента, цезий и рубидий.

Густав Кирхгоф (слева) и Роберт Бунзен (справа)

Кирхгоф позже применил свою теорию спектрального анализа к изучению состава Солнца, где он обнаружил множество темных линий в спектре длин волн Солнца.Это было вызвано тем, что газ Солнца поглощал световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.

Немного ближе к дому в мире электроники, Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа строится на основе, изложенной в законе Ома, и помогла проложить путь для анализа сложных схем, на который мы полагаемся сегодня.

Первый закон — Действующий закон Кирхгофа

Закон Кирхгофа по току гласит, что величина тока, входящего в узел, равна величине тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выходить наружу. Вы можете определить узел, в котором два или более пути соединены общей точкой. На схеме это будет точка соединения, соединяющая две пересекающиеся сетевые соединения.

Взгляните на изображение ниже, чтобы наглядно понять этот Закон.Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону тока Кирхгофа, взаимосвязь между этими токами, входящими в узел и выходящими из него, может быть представлена ​​как I 1 + I 2 = I 3 + I 4 + I 5 .

Текущий закон Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)

Когда вы уравновешиваете это уравнение как алгебраическое выражение, вы делаете вывод, что ток на входе и выходе из узла всегда будет равен 0, или I 1 + I 2 + (-I 3 + -I 4 + -I 5 ) = 0 Все должно уравновешиваться, и Кирхгоф назвал этот принцип Сохранением заряда .

Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже представлена ​​схема с четырьмя узлами: A, C, E и F. Сначала ток течет от источника напряжения и отделяется в узле A, а затем протекает через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы протекать через резисторы R3, R4 и R5, где он встречается с узлом E и узлом F.

(Источник изображения)

Чтобы подтвердить закон Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:

1. Рассчитать полный ток цепи
2. Рассчитать ток, протекающий через каждый узел
3. Сравните входные и выходные токи в определенных узлах, чтобы подтвердить закон Кирхгофа о токе.

1. Рассчитайте общий ток

Здесь мы используем закон Ома, чтобы получить полный ток нашей цепи с I = V / R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, подключенных параллельно, которое составляет:

Начиная с узла AC, получаем следующее сопротивление для параллельных резисторов R1 и R2:

И переходя к узлу CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:

Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы можем затем подключить к закону Ома I = V / R , чтобы получить общий ток в нашей цепи:

2.Расчет узловых токов

Теперь, когда мы знаем, что из нашей цепи выходит 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся помощью закона Ома в форме I = V / R , чтобы получить ток для каждой ветви узла.

Для начала нам нужны напряжения для узловых ветвей AC и CF:

Затем мы можем рассчитать ток для каждой ветви узла:

3. Подтвердите действующий закон Кирхгофа

После вычисления тока для каждой ветви узла у нас теперь есть две отдельные контрольные точки, которые мы можем использовать для сравнения наших входных и выходных токов.Это позволит нам проанализировать нашу схему и подтвердить текущий закон Кирхгофа следующим образом:

Второй закон — Закон Кирхгофа о напряжении

Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром полное напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что падение напряжения происходит всякий раз, когда ток проходит через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Сохранением энергии .Опять же, то, что входит, должно выходить наружу.

Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение встретит пассивный компонент, что вызовет заметное падение напряжения.

Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:

Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает.В приведенном ниже примере у нас есть две известные переменные: полное напряжение и падение напряжения на R1.

(Источник изображения)

Что нам нужно вычислить, так это падение напряжения на R2, и мы можем использовать закон Кирхгофа, чтобы вычислить это со следующей зависимостью:

Поскольку полное падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления нашей недостающей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:

Давайте посмотрим на другой пример.В схеме ниже у нас есть три резистора, подключенных последовательно с батареей на 12 В.

Чтобы проверить закон напряжения Кирхгофа в этой цепи, нам нужно предпринять следующие шаги:

1. Вычислить полное сопротивление цепи
2. Вычислить полный ток цепи
3. Рассчитайте ток через каждого резистора
4. Рассчитайте падение напряжения на каждом резисторе

Сравните источник напряжения с общим падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении

1.Рассчитайте общее сопротивление

Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:

2. Рассчитайте общий ток

Теперь, когда мы знаем наше полное сопротивление, мы снова можем использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V / R, , который выглядит так:

3. Рассчитайте ток через каждый резистор

Поскольку все наши резисторы соединены последовательно, через них будет протекать одинаковый ток, который мы можем выразить как:

4.Рассчитайте падение напряжения на каждом резисторе

.

В нашем окончательном расчете мы снова будем использовать закон Ома, чтобы получить полное падение напряжения для каждого резистора в виде В = IR , которое выглядит следующим образом:

5. Подтвердите закон Кирхгофа о напряжении

Теперь у нас есть все необходимые данные, включая общее напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собирая все это вместе, мы можем легко проверить закон напряжения Кирхгофа с помощью следующего соотношения:

Это также можно выразить как:

Как видите, полное напряжение равно общему падению напряжения в нашей цепи.То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!

Процесс использования закона Кирхгофа об округах

Поняв, как работает закон Кирхгофа, в вашем наборе инструментов теперь есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих Законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:

1. Во-первых, начните с маркировки всех известных напряжений и сопротивлений вашей цепи.
2. Затем назовите каждую ветвь в вашей цепи текущей меткой, например I1, I2, I3 и т. Д.Ветвь — это один или группа компонентов, соединенных между двумя узлами.
3. Затем найдите текущий закон Кирхгофа для каждого узла в вашей цепи.
4. Затем найдите закон напряжения Кирхгофа для каждого из независимых контуров в вашей цепи.

После того, как вы рассчитали законы Кирхгофа по току и напряжению, вы можете использовать свои уравнения, чтобы найти недостающие токи. Готовы попробовать это самостоятельно? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон тока Кирхгофа и закон напряжения с небольшой помощью Ома!

Свои ответы оставляйте в комментариях ниже!

Стоя на плечах Ома

Имея в руках Закон Кирхгофа о цепях, теперь у вас есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было до него — закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем, основываясь на этих расчетах с законом Кирхгофа, увидите, соответствует ли ваша схема этим принципам тока и напряжения.

Готовы применить закон Кирхгофа в своем собственном проекте электронного дизайна? Попробуйте Autodesk EAGLE бесплатно сегодня!

Интегралы в электрических цепях

Производные и интегралы широко используются для описания переходных процессов в электрических цепях.Ниже мы рассмотрим некоторые типичные проблемы, которые можно решить с помощью интеграции. Ограничимся рассмотрением схем первого порядка.

Связь между зарядом и током

Электрический ток \ (I \) определяется как скорость потока заряда \ (Q \) и выражается производной

\ [I \ left (t \ right) = \ frac {{dQ \ left (t \ right)}} {{dt}}. t {I \ left (s \ right) ds}, \]

где \ (C \) — значение емкости, \ (s \) — внутренняя переменная интегрирования.{- \ frac {t} {{RC}}}}. \]

Рисунок 2.

Постоянная времени \ (\ tau = RC \) здесь определяет, насколько быстро происходит переходный процесс в цепи.

RL Схема

В простой цепи RL последовательно соединены резистор и катушка индуктивности.

Рисунок 3.

Когда переключатель в момент времени \ (t = 0 \) замкнут, применяется постоянная ЭДС \ (\ varepsilon \), и ток \ (I \) начинает течь по цепи.

Как и в предыдущем разделе, напряжение на резисторе равно

.

\ [{V_R} \ left (t \ right) = I \ left (t \ right) R.\]

Напряжение на катушке индуктивности выражается производной

\ [{V_L} \ left (t \ right) = L \ frac {{dI}} {{dt}}. \]

Так, по КВЛ,

\ [{V_R} \ left (t \ right) + {V_L} \ left (t \ right) = \ varepsilon, \]

или

\ [RI \ left (t \ right) + L \ frac {{dI}} {{dt}} = \ varepsilon. {- \ frac {R} {L} t}}} \ right).\]

Рис. 4.

Мы видим, что постоянная времени для цепи RL определяется выражением \ (\ tau = \ large {\ frac {L} {R}} \ normalsize. \)

Мощность и энергия

Электрическая энергия \ (E, \), измеряемая в джоулях (Дж), представляет собой форму энергии, которая возникает из кинетической или потенциальной энергии, которой обладают электрические заряды.

Электрическая мощность \ (P, \), измеряемая в ваттах (Вт), — это скорость, с которой электрическая энергия передается по электрической цепи.

Мощность, рассеиваемая в элементе цепи постоянного тока \ (\ left ({DC} \ right) \), определяется формулой

\ [P = VI, \]

где \ (V \) — напряжение на элементе, а \ (I \) — ток в цепи.t {V \ left (s \ right) I \ left (s \ right) ds}, \]

где \ (s \) — внутренняя переменная интегрирования.

Энергия, запасенная в конденсаторе

Перемещение небольшого заряда \ (dq \) с одной пластины конденсатора на другую требует работы

\ [dW = Vdq = \ frac {q} {C} dq, \]

где \ (C \) — емкость, а \ (q \) — текущий заряд конденсатора. 2}}} {2}.2} — 4, & t \ gt 3
\ end {case}, \]
где ток \ (I \) измеряется в \ (A \), а время \ (t \) измеряется в \ ({сек}. \). Найдите общий заряд, попавший в элемент за время \ (T = 6 \, с. \)

Пример 2

Ток в цепи увеличивается линейно во времени как \ (I \ left (t \ right) = \ alpha t \) в течение временного интервала \ (\ left [{0, T} \ right] \) и вызывает резистор \ (R \), чтобы нагреться. Предполагая, что процесс нагрева является адиабатическим, определите, как изменение температуры резистора \ (\ Delta T \) зависит от скорости \ (\ alpha.\) Удельная теплоемкость материала резистора \ (c, \), масса резистора \ (m. \)

Пример 3

Предположим, конденсатор \ (C \) заряжается от источника с постоянной ЭДС \ (\ varepsilon. \). Вычислите тепловую энергию, рассеиваемую резистором \ (R \) за время зарядки.

Пример 4

Когда переключатель замкнут в момент времени \ (t = 0, \), начальный ток в цепи без источника \ (RL \) равен \ ({I_0} = 1 \, A. \) Найдите энергию \ ({E_R } \) рассеивается резистором между \ (t = 0 \) и \ (T = 1 \, ms, \), если \ (R = 50 \, k \ Omega, \) \ (L = 0.{- 100t}} \, \ left (V \ right).} \]
Определите полную энергию, рассеиваемую элементом между \ (t = 0 \) и \ (t = 10 \, {ms}. \)

Пример 6

В момент времени \ (t = 0, \) ЭДС \ (\ varepsilon = 50 \, V \) применяется к первоначально незаряженному конденсатору \ (C = 10 \, \ mu F. \). Конденсатор начинает заряжаться через резистор \ (R = 100 \, k \ Omega. \) Определите количество электронов на отрицательной пластине конденсатора за \ (1 \) секунду.

Пример 7

Ток и напряжение на элементе схемы изменяются по синусоидальному закону:
\ [{I \ left (t \ right) = {I_0} \ sin \ left ({\ frac {{2 \ pi t}} {T} + \ theta} \ right), \; \;} \ kern0pt { V \ left (t \ right) = {V_0} \ sin \ left ({\ frac {{2 \ pi t}} {T}} \ right),} \]
где \ (T \) — период колебаний, \ (\ theta \) — разность фаз, \ ({I_0} \) и \ ({V_0} \) — начальные значения тока и напряжения. 2} — 4, & t \ gt 3
\ end {case}, \]
где ток \ (I \) измеряется в \ (A \), а время \ (t \) измеряется в \ ({сек}.6} = {9 + \ left ({\ frac {{216}} {3} — 4} \ right) — \ left ({3 — 12} \ right)} = {60 \, C}. \]

Пример 2.

Ток в цепи увеличивается линейно во времени как \ (I \ left (t \ right) = \ alpha t \) в течение временного интервала \ (\ left [{0, T} \ right] \) и вызывает резистор \ (R \), чтобы нагреться. Предполагая, что процесс нагрева является адиабатическим, определите, как изменение температуры резистора \ (\ Delta T \) зависит от скорости \ (\ alpha. \). Удельная теплоемкость материала резистора равна \ (c, \) масса резистора \ (м.2}. \]

Таким образом, изменение температуры \ (\ Delta \ theta \) пропорционально квадрату текущей скорости \ (\ alpha \).

Пример 3.

Предположим, конденсатор \ (C \) заряжается от источника с постоянной ЭДС \ (\ varepsilon. \). Вычислите тепловую энергию, рассеиваемую резистором \ (R \) за время зарядки. {- \ frac {t } {{RC}}}}.{15}}} \]

Пример 7.

Ток и напряжение на элементе схемы изменяются по синусоидальному закону:
\ [{I \ left (t \ right) = {I_0} \ sin \ left ({\ frac {{2 \ pi t}} {T} + \ theta} \ right), \; \;} \ kern0pt { V \ left (t \ right) = {V_0} \ sin \ left ({\ frac {{2 \ pi t}} {T}} \ right),} \]
где \ (T \) — период колебаний, \ (\ theta \) — разность фаз, \ ({I_0} \) и \ ({V_0} \) — начальные значения тока и напряжения. Найдите среднюю мощность, рассеиваемую в элементе схемы за период одного цикла.T {\ sin \ left ({\ frac {{2 \ pi t}} {T} + \ theta} \ right) \ sin \ left ({\ frac {{2 \ pi t}} {T}} \ right ) dt}.} \]

Использование идентичности произведения на сумму

\ [{\ sin \ alpha \ sin \ beta \ text {=}} \ kern0pt {\ frac {1} {2} \ left [{\ cos \ left ({\ alpha — \ beta} \ right) — \ cos \ left ({\ alpha + \ beta} \ right)} \ right],} \]

подынтегральное выражение можно переписать в виде

\ [{\ sin \ left ({\ frac {{2 \ pi t}} {T} + \ theta} \ right) \ sin \ left ({\ frac {{2 \ pi t}} {T}}) \ right)} = {\ frac {1} {2} \ left [{\ cos \ left ({- \ theta} \ right) — \ cos \ left ({\ frac {{4 \ pi t}}} {T } + \ theta} \ right)} \ right]} = {\ frac {1} {2} \ left [{\ cos \ theta — \ cos \ left ({\ frac {{4 \ pi t}} {T } + \ theta} \ right)} \ right].T} = {\ frac {{{I_0} {V_0}}} {2} \ left [{\ cos \ theta — \ underbrace {\ frac {{\ sin \ left ({4 \ pi + \ theta} \ right ) — \ sin \ theta}} {{4 \ pi}}} _ 0} \ right]} = {\ frac {{{I_0} {V_0} \ cos \ theta}} {2}.} \]

Как видите, максимальная средняя мощность достигается при \ (\ theta = 0: \)

\ [{{\ bar P} _ {\ max}} = \ frac {{{I_0} {V_0}}} {2}. \]

Пример 8.

Источник постоянной ЭДС \ (\ varepsilon = 100 \, V \) подключается к цепи с начальным сопротивлением \ ({R_0} = 20 \, \ Omega.\) Рассчитайте заряд \ (Q \), который будет проходить в цепи в течение \ (T = 1 \, min, \), если сопротивление линейно увеличивается со скоростью \ (\ alpha = 1 \ large {\ frac {\ Омега} {s}} \ normalsize. \)

Решение.

Сопротивление \ (R \) цепи изменяется по закону

\ [R \ left (t \ right) = {R_0} + \ alpha t. \]

По закону Ома,

\ [I \ left (t \ right) = \ frac {\ varepsilon} {{R \ left (t \ right)}} = \ frac {\ varepsilon} {{{R_0} + \ alpha t}}. \ ]

Чтобы найти заряд \ (Q, \), мы интегрируем ток \ (I \ left (t \ right) \) за временной интервал \ (\ left [{0, T} \ right], \), где \ ( T = 1 \, min = 60 \, с.T} = {\ frac {\ varepsilon} {\ alpha} \ left [{\ ln \ left ({{R_0} + \ alpha T} \ right) — \ ln {R_0}} \ right]} = {\ frac {\ varepsilon} {\ alpha} \ ln \ frac {{{R_0} + \ alpha T}} {{{R_0}}}} = {\ frac {\ varepsilon} {\ alpha} \ ln \ left ({1 + \ frac {{\ alpha T}} {{{R_0}}}} \ right).} \]

Подставляя указанные значения, получаем

\ [{Q = \ frac {\ varepsilon} {\ alpha} \ ln \ left ({1 + \ frac {{\ alpha T}} {{{R_0}}}} \ right)} = {\ frac { {100}} {1} \ ln \ left ({1 + \ frac {{1 \ times 60}} {{20}}} \ right)} \ приблизительно {138.6 \, C} \]

Ток и напряжение — AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.