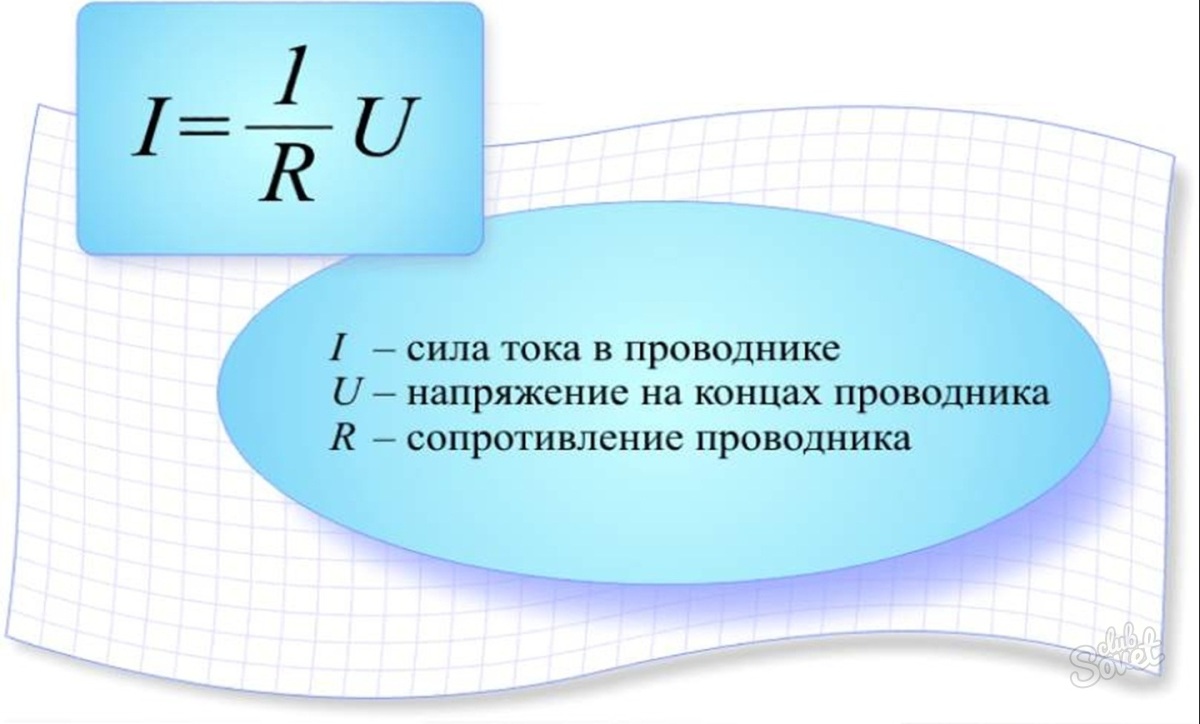
Основные расчетные электротехнические формулы
Электрическое сопротивление материала определяется по формулам:
Электрическое сопротивление, Ом, материала
R = U/I, где U — напряжение, В; I — сила тока, А.
Удельное электрическое сопротивление, Ом·м,
ρ=Rs/l. S – сечение проводника, м² ; l – длина проводника, м.
Под удельным электрическим сопротивлением материала понимают сопротивление проводника длиной 1 м и сечением
1 м² при 20°С.
Величина, обратная удельному сопротивлению, называется проводимостью:
v=1/ρ.
Если вместо сечения проводника S задан его диаметр D, то сечение, м², находят по формуле
S= πD²/4, где π =3,14.
Сопротивление материала зависит от температуры. Если материал нагрет до температуры t°С, то его
сопротивление, Ом, при этой температуре равно:
Rt= R0[1 + α (t – t0)],
где R0 – сопротивление при начальной температуре t0°С, Ом; α – температурный коэффициент.
Далее приводятся значения α для различных материалов.
| Медь, алюминий, вольфрам | 0,004 |
| Сталь | 0,006 |
| Латунь | 0,002 |
Сопротивление нескольких проводников зависит от способа их соединения. Например, при параллельном
соединении сопротивление трех проводников определяется по формуле:
Rоб=R1*R2*R3/(R1R2+R2R3+R3R1)
При последовательном соединении:
Rоб=R1+R2+R3.
Постоянный ток
Постоянный ток применяют для питания устройств связи, транзисторных приборов, стартеров автомобилей,
электрокар, а также, для зарядки аккумуляторов.
В качестве источников постоянного тока используют гальванические элементы, солнечные батареи,
термоэлектрогенераторы, генераторы постоянного тока.
При параллельном соединении нескольких проводников с током с равными напряжениями:
Iоб = I1+I2+…+In Uоб=U1=U2=…=Un
При последовательном соединении: Iоб = Imin; – где Imin, ток наименьшего по мощности источника тока
(генератора, аккумуляторной батареи).
Uоб = U1+U2+…+Un
Основные параметры цепей однофазного переменного тока
Однофазный переменный ток промышленной частоты имеет 50 периодов колебаний в секунду, или 50 Гц. Его
применяют для питания небольших вентиляторов, электробытовых приборов, электроинструмента, при электросварке
и для питания большинства осветительных приборов.
Частота переменного тока, Гц:
f= 1/T = np/60, где п — частота вращения генератора, мин -1; р – число пар полюсов
генератора.
Мощность однофазного переменного тока:
активная, Вт, Ра = IUcosφ;
реактивная, вар, Q = IUsinφ;
кажущаяся, В А, S = IU =√ (P 2α+Q 2)
Если в цепь переменного однофазного тока включено только активное сопротивление (например, нагревательные
элементы или электрические лампы), то значение силы тока и мощности в каждый момент времени определяют по
закону Ома:
I=U/R; Рa = IU = I²R=U²/R.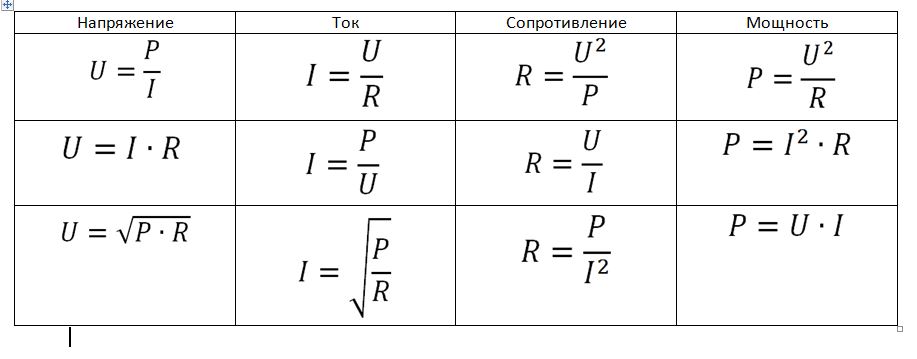
Коэффициент мощности в цепи с индуктивной нагрузкой
Cosφ= Рa/IU= Рa/S.
Основные параметры цепей трехфазного переменного тока
Трехфазный переменный ток используют для питания большинства промышленных электроприемников. Частота
трехфазного переменного тока 50 Гц.
В трехфазных системах обмотки генератора и электроприемника соединяют по схемам «звезда» или «треугольник».
При соединении в звезду концы всех трех обмоток генератора (или электроприемника) объединяют в общую точку,
называемую нулевой или нейтралью (рис. 5а).
При соединении в треугольник начало первой обмотки соединяют с концом второй, начало второй обмотки — с
концом третьей и начало третьей — с концом первой обмотки (рис. 5б).
Если от генератора отходят только три провода, то такая система называется трехфазной трехпроводной; если
от него отходит еще и четвертый нулевой провод, то систему называют трехфазной четырехпроводной.
Трехфазные трехпроводные сети используют для питания трехфазных силовых потребителей, а четырехпроводные
сети – для питания преимущественно осветительных и бытовых нагрузок.
В трехфазных системах различают фазные и линейные токи и напряжения. При соединении фаз звездой линейный I
и фазный Iφ токи равны:
а напряжение U =√3Uφ
При соединении треугольником
I =√3Iφ
а напряжение U = Uφ.
Мощность переменного трехфазного тока:
генератора:
- активная, Вт, Рг =√3IUcosφ ,
- реактивная, вар, Q=√3IUsinφ
- полная, ВА, S = √3IU.
где φ – угол сдвига фаз между фазным напряжением генератора и током в той же фазе приемника, который
равен току в линии при соединении обмоток генератора звездой.
приемника:
- активная, Вт, Рп =3UφIcosφп=√3 IUcosφп ,
- реактивная, вар, Q=√3 UφIsinφп=√3 UIsinφ
- полная, ВА, S = √3UI.

где φ – угол сдвига фаз между фазным напряжением приемника и током в той же фазе приемника, который
равен току линейному только при соединении звездой.
Подсчет количества теплоты, выделяемой при протекании электрического тока по проводнику.
Количество теплоты, Дж, выделяемой электрическим током в проводнике,
Q=I²Rt где t — время, с.
При определении теплового действия электрического тока учитывают, что 1 кВт·ч выделяет 864 ккал (3617 кДж).
Если у Вас остались вопросы – обращайтесь к нам, в авторизованный сервисный центр “Эл
Ко-сервис” Мы всегда рады помочь Вам в решении возникших у Вас проблем.
Инженерно-технический отдел авторизованного сервисного центра “Эл Ко-сервис”
Мощность электрического тока: особенности и измерения
Мощность электрического тока – скорость выполняемой цепью работы. Простое определение, морока с пониманием. Мощность подразделяется на активную, реактивную.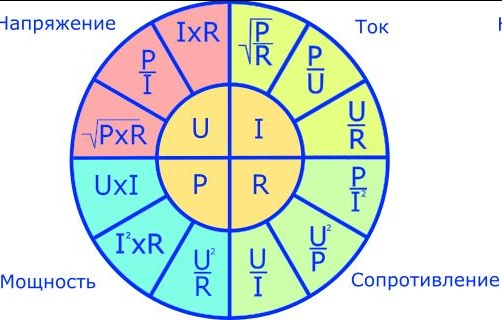 И начинается…
И начинается…
Работа электрического тока, мощность
При движении заряда по проводнику поле выполняет над ним работу. Величина характеризуется напряжением, в отличие от напряженности в свободном пространстве. Заряды двигаются в сторону убывания потенциалов, для поддержания процесса требуется источник энергии. Напряжение численно равно работе поля при перемещении на участке единичного заряда (1 Кл). В ходе взаимодействий электрическая энергия переходит в другие виды. Поэтому необходим ввод универсальной единицы, физической свободно конвертируемой валюты. В организме мерой выступает АТФ, электричестве — работа поля.
Электрическая дуга
На схеме момент превращения энергии отображается в виде источников ЭДС. Если у генераторов направлены в одну сторону, у потребителя – обязательно в другую. Наглядным фактом отражается процесс расхода мощности, отбора у источников энергии. ЭДС несет обратный знак, часто называется противо-ЭДС. Избегайте путать понятие с явлением, возникающим в индуктивностях при выключении питания. Противо-ЭДС означает переход электрической энергии в химическую, механическую, световую.
Противо-ЭДС означает переход электрической энергии в химическую, механическую, световую.
Потребитель хочет выполнить работу за некоторую единицу времени. Очевидно, газонокосильщик не намерен ждать зимы, надеется управиться к обеду. Мощность источника должна обеспечить заданную скорость выполнения. Работу осуществляет электрический ток, следовательно, понятие также относится. Мощность бывает активной, реактивной, полезной и мощностью потерь. Участки, обозначаемые физическими схемами сопротивлениями, на практике вредны, являются издержками. На резисторах проводников выделяется тепло, эффект Джоуля-Ленца ведет к лишнему расходу мощности. Исключением назовем нагревательные приборы, где явление желательно.
Полезная работа на физических схемах обозначается противо-ЭДС (обычный источник с обратным генератору направлением). Для мощности имеется несколько аналитических выражений. Иногда удобно использовать одно, в других случаях – иное (см. рис.):
Выражения мощности тока
- Мощность – скорость выполнения работы.

- Мощность равна произведению напряжения на ток.
- Мощность, затрачиваемая на тепловое действие, равна произведению сопротивления на квадрат тока.
- Мощность, затрачиваемая на тепловое действие, равна отношению квадрата напряжения к сопротивлению.
Запасшемуся токовыми клещами проще использовать вторую формулу. Вне зависимости от характера нагрузки посчитаем мощность. Только активную. Мощность определена многими факторами, включая температуру. Под номинальным для прибора значением понимаем, развиваемое в установившемся режиме. Для нагревателей следует применять третью, четвертую формулу. Мощность зависит целиком и полностью от параметров питающей сети. Предназначенные для работы со 110 вольт переменного тока в европейских условиях быстро сгорят.
Трехфазные цепи
Новичкам трехфазные цепи представляются сложными, на деле это более элегантное техническое решение. Даже электричество домом поставляют тремя линиями. Внутри подъезда делят по квартирам. Больше смущает то, что некоторые приборы на три фазы лишены заземления, нулевого провода. Схемы с изолированной нейтралью. Нулевой провод не нужен, ток возвращается источнику по фазным линиям. Разумеется, нагрузка здесь на каждую жилу повышенная. Требования ПУЭ отдельно оговаривают род сети. Для трехфазных схем вводятся следующие понятия, о которых нужно иметь представление, чтобы правильно посчитать мощность:
Больше смущает то, что некоторые приборы на три фазы лишены заземления, нулевого провода. Схемы с изолированной нейтралью. Нулевой провод не нужен, ток возвращается источнику по фазным линиям. Разумеется, нагрузка здесь на каждую жилу повышенная. Требования ПУЭ отдельно оговаривают род сети. Для трехфазных схем вводятся следующие понятия, о которых нужно иметь представление, чтобы правильно посчитать мощность:
Трехфазная цепь с изолированной нейтралью
- Фазным напряжением, током называют, соответственно, разницу потенциалов и скорость передвижения заряда меж фазой и нейтралью. Понятно, в оговоренном выше случае с полной изоляцией формулы будут недействительны. Поскольку нейтрали нет.
- Линейным напряжением, током называют, соответственно, разницу потенциалов или скорость перемещения заряда меж любыми двумя фазами. Номера понятны из контекста. Когда говорят о сетях 400 вольт, подразумевают три провода, разница потенциалов с нейтралью равна 230 вольт. Линейное напряжение выше фазного.

Меж напряжением и током существует сдвиг фаз. О чем умалчивает школьная физика. Фазы совпадают, если нагрузка 100% активная (простые резисторы). Иначе появляется сдвиг. В индуктивности ток отстает от напряжения на 90 градусов, в емкости – опережает. Простая истина легко запоминается следующим образом (плавно подходим к реактивной мощности). Мнимая часть сопротивления индуктивности составляет jωL, где ω – круговая частота, равная обычной (в Гц), помноженной на 2 числа Пи; j – оператор, обозначающий направление вектора. Теперь пишем закон Ома: U = I R = I jωL.
Из равенства видно: напряжение нужно отложить вверх на 90 градусов при построении диаграммы, ток останется на оси абсцисс (горизонтальная ось Х). Вращение по правилам радиотехники происходит против часовой стрелки. Теперь очевиден факт: ток отстает на 90 градусов. По аналогии проведем сравнение для конденсатора. Сопротивление переменному току в мнимой форме выглядит так: -j/ωL, знак указывает: откладывать напряжение нужно будет вниз, перпендикулярно оси абсцисс. Следовательно, ток опережает по фазе на 90 градусов.
Следовательно, ток опережает по фазе на 90 градусов.
В реальности параллельно с мнимой частью присутствует действительная – называют активным сопротивлением. Проволока катушки представлена резистором, будучи свитой, приобретает индуктивные свойства. Поэтому реальный угол фаз будет не 90 градусов, немного меньше.
А теперь можно переходить к формулам мощности тока трехфазных цепей. Здесь линия формирует сдвиг фаз. Меж напряжением и током, и относительно другой линии. Согласитесь, без заботливо изложенных авторами знания факт нельзя осознать. Меж линиями промышленной трехфазной сети сдвиг 120 градусов (полный оборот – 360 градусов). Обеспечит равномерность вращения поля в двигателях, для рядовых потребителей безразличен. Так удобнее генераторам ГЭС – нагрузка сбалансированная. Сдвиг идет меж линиями, в каждой ток опережает напряжение или отстает:
- Если линия симметричная, сдвиги меж любыми фазами по току составляют 120 градусов, формула получается предельно простой.
 Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока.
Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока. - Вторая группа формул приведена для трехфазных цепей с изолированной нейтралью. Предполагается, ток одной линии утекает по другой. Нейтраль отсутствует за ненадобностью. Поэтому напряжения берутся не фазные (не от чего отсчитывать), как предыдущей формулой, а линейные. Соответственно, цифры показывают, какой параметр следует взять. Повремените пугаться греческих букв – фазы меж двумя перемножаемыми параметрами. Цифры меняются местами (1,2 или 2,1), чтобы правильно учесть знак.
- В асимметричной цепи вновь появляются фазные напряжение, ток. Здесь расчет ведется отдельно для каждой линии. Никаких вариантов нет.

Формулы мощности тока
На практике измерить мощность тока
Намекнули, можно воспользоваться токовыми клещами. Прибор позволит определить крейсерские параметры дрели. Разгон можно засечь только при многократных опытах, процесс чрезвычайно быстрый, частота смены индикации не выше 3-х раз в секунду. Токовые клещи демонстрируют погрешность. Практика показывает: достичь погрешности, указанной в паспорте, сложно.
Чаще для оценки мощности используют счетчики (для выплат компаниям-поставщикам), ваттметры (для личных и рабочих целей). Стрелочный прибор содержит пару неподвижных катушек, по которым течет ток цепи, подвижную рамку, для заведения напряжения путем параллельного включения нагрузки. Конструкция рассчитана сразу реализовать формулу полной мощности (см. рис.). Ток умножается на напряжение и некий коэффициент, учитывающий градуировку шкалы, также на косинус сдвига фаз между параметрами. Как говорили выше, сдвиг умещается в пределах 90 – минус 90 градусов, следовательно, косинус положителен, крутящий момент стрелки направлен в одну сторону.
Отсутствует возможность сказать индуктивная ли нагрузка или емкостная. Зато при неправильном включении в цепь показания будут отрицательными (завал набок). Произойдет аналогичное событие, если потребитель вдруг станет отдавать мощность обратно нагрузке (бывает такое). В современных приборах происходит нечто подобное же, вычисления ведет электронный модуль, интегрирующий расход энергии, либо считывающий показания мощности. Вместо стрелки присутствует электронный индикатор и множество других полезных опций.
Особые проблемы вызывают измерения в асимметричных цепях с изолированной нейтралью, где нельзя прямо складывать мощности каждой линии. Ваттметры делятся принципом действия:
- Электродинамические. Описаны разделом. Состоят из одной подвижной, двух неподвижных катушек.
- Ферродинамические. Напоминает двигатель с расщепленным полюсом (shaded-pole motor).

- С квадратором. Используется амплитудно-частотная характеристика нелинейного элемента (например, диода), напоминающая параболу, для возведения электрической величины в квадрат (используется в вычислениях).
- С датчиком Холла. Если индукцию сделать при помощи катушки пропорциональной напряжению магнитного поля в сенсоре, подать ток, ЭДС будет результатом умножения двух величин. Искомая величина.
- Компараторы. Постепенно повышает опорный сигнал, пока не будет достигнуто равенство. Цифровые приборы достигают высокой точности.
В цепях с сильным сдвигом фаз для оценки потерь применяется синусный ваттметр. Конструкция схожа с рассмотренной, пространственное положение таково, что вычисляется реактивная мощность (см. рис.). В этом случае произведение тока и напряжения домножим на синус угла сдвига фаз. Реактивную мощность измерим обычным (активным) ваттметром. Имеется несколько методик. Например, в трехфазной симметричной цепи нужно последовательную обмотку включить в одну линию, параллельную – в две другие. Затем производятся вычисления: показания прибора умножаются на корень из трех (с учетом, что на индикаторе произведение тока, напряжения и синуса угла между ними).
Затем производятся вычисления: показания прибора умножаются на корень из трех (с учетом, что на индикаторе произведение тока, напряжения и синуса угла между ними).
Методика двух ваттметров
Для трехфазной цепи с простой асимметрией задача усложняется. На рисунке показана методика двух ваттметров (ферродинамических или электродинамических). Начала обмоток указаны звездочками. Ток проходит через последовательные, напряжение с двух фаз подается на параллельную (одно через резистор). Алгебраическая сумма показаний обоих ваттметров складывается, умножается на корень из трех для получения значения реактивной мощности.
Работа и мощность тока
У каждого из нас дома есть счетчик, по показаниям которого мы ежемесячно платим за электричество. Мы оплачиваем какое-то количество киловатт-часов. Что же такое эти киловатт-часы? За что конкретно мы платим? Разберемся 🙂
Мы используем электричество с определенными целями. Электрический ток выполняет какую-то работу, вследствие этого и функционируют наши электроприборы. Что же такое – работа электрического тока? Известно, что работа тока по перемещению электрического заряда на некотором отрезке цепи равна численно напряжению на этом участке. Если же заряд будет отличаться, например, в большую сторону, то и работа, соответственно, будет совершена большая.
Работа тока на участке цепи: формула
Итак, мы приходим к тому, что работа тока равна произведению напряжения на участке электрической цепи на величину заряда. Заряд же, как известно, можно найти произведением силы тока на время прохождения тока. Итак, получаем формулу для определения работы тока:
A=Uq , q=It , получаем A=UIt ;
где A — работа, U- напряжение, I — сила тока, q — заряд, t — время.
Измеряется работа тока в джоулях (1 Дж). 1 Дж = 1 В * 1 А * 1 с. То есть, чтобы измерить работу, которую совершил ток, нам нужны три прибора: амперметр, вольтметр и часы. Счетчики электроэнергии, которые стоят в квартирах, как бы сочетают в себе все эти вышеперечисленные приборы в одном. Они измеряют работу, совершенную током. Работа тока в нашей квартире – это энергия, которую он израсходовал на всех включенных в сеть квартиры приборах. Это и есть то, за что мы платим. Однако, мы платим не за джоули, а за киловатт-часы. Откуда возникают эти единицы?
Мощность электрического тока
Чтобы разобраться с этим вопросом, надо рассмотреть еще одно понятие — мощность электрического тока. Мощность тока – это работа тока, совершенная в единицу времени. То есть, мощность можно найти, разделив работу на время. А работа, как мы уже знаем – это произведение силы тока на напряжение и на время. Таким образом, время сократится, и мы получим произведение силы тока на напряжение. Для мощности тока формула будет иметь следующий вид:
P=A/t , A=UIt , получаем P=UIt/t , то есть P=UI ;
где P — мощность тока. Мощность измеряется в ваттах (1 Вт). Применяют кратные величины – киловатты, мегаватты.
Работа и мощность электрического тока связаны теснейшим образом. Фактически, работа – это мощность тока в каждый момент времени, взятая за определенный промежуток времени. Именно поэтому счетчики в квартирах измеряют работу тока не в джоулях, а в киловатт-часах. Просто величина мощности в 1 ватт – это очень небольшая мощность, и если бы мы платили за ватты-в-секунду, мы бы оплачивали десятки и сотни тысяч таких единиц. Для упрощения расчетов и приняли единицу «киловатт-час».
Нужна помощь в учебе?
Предыдущая тема: Последовательное и параллельное соединение проводников
Следующая тема:   Закон Джоуля-Ленца: работа тока равна количеству теплоты
Что такое напряжение, ток, сопротивление: разбираемся на примерах
Не имея определенных начальных знаний об электричестве, тяжело себе представить, как работают электрические приборы, почему вообще они работают, почему надо включать телевизор в розетку, чтобы он заработал, а фонарику хватает маленькой батарейки, чтобы он светил в темноте.
И так будем разбираться во всем по порядку.
Электричество
Электричество – это природное явление, подтверждающее существование, взаимодействие и движение электрических зарядов. Электричество впервые было обнаружено еще в VII веке до н.э. греческим философом Фалесом. Фалес обратил внимание на то, что если кусочек янтаря потереть о шерсть, он начинает притягивать к себе легкие предметы. Янтарь на древнегреческом – электрон.
Вот так и представляю себе, сидит Фалес, трет кусок янтаря о свой гиматий (это шерстяная верхняя одежда у древних греков), а затем с озадаченным видом смотрит, как к янтарю притягиваются волосы, обрывки ниток, перья и клочки бумаги.
Данное явление называется статическим электричеством. Вы можете повторить данный опыт. Для этого хорошенько потрите шерстяной тканью обычную пластмассовую линейку и поднесите ее к мелким бумажным кусочкам.
Следует отметить, что долгое время это явление не изучалось. И только в 1600 году в своем сочинении «О магните, магнитных телах и о большом магните – Земле» английский естествоиспытатель Уильям Гилберт ввел термин – электричество. В своей работе он описал свои опыты с наэлектризованными предметами, а также установил, что наэлектризовываться могут и другие вещества.
Далее на протяжении трех веков самые передовые ученые мира исследуют электричество, пишут трактаты, формулируют законы, изобретают электрические машины и только в 1897 году Джозеф Томсон открывает первый материальный носитель электричества – электрон, частицу, благодаря которой возможны электрические процессы в веществах.
Электрон – это элементарная частица, имеет отрицательный заряд примерно равный -1,602·10-19 Кл (Кулон). Обозначается е или е–.
Напряжение
Чтобы заставить перемещаться заряженные частицы от одного полюса к другому необходимо создать между полюсами разность потенциалов или – Напряжение. Единица измерения напряжения – Вольт (В или V). В формулах и расчетах напряжение обозначается буквой V. Чтобы получить напряжение величиной 1 В нужно передать между полюсами заряд в 1 Кл, совершив при этом работу в 1 Дж (Джоуль).
Для наглядности представим резервуар с водой расположенный на некоторой высоте. Из резервуара выходит труба. Вода под естественным давлением покидает резервуар через трубу. Давайте условимся, что вода – это электрический заряд, высота водяного столба (давление) – это напряжение, а скорость потока воды – это электрический ток.
Таким образом, чем больше воды в баке, тем выше давление. Аналогично с электрической точки зрения, чем больше заряд, тем выше напряжение.
Начнем сливать воду, давление при этом будет уменьшаться. Т.е. уровень заряда опускается – величина напряжения уменьшается. Такое явление можно наблюдать в фонарике, лампочка светит все тусклее по мере того как разряжаются батарейки. Обратите внимание, чем меньше давление воды (напряжение), тем меньше поток воды (ток).
Электрический ток
Электрический ток – это физический процесс направленного движения заряженных частиц под действием электромагнитного поля от одного полюса замкнутой электрической цепи к другому. В качестве частиц, переносящих заряд, могут выступать электроны, протоны, ионы и дырки. При отсутствии замкнутой цепи ток невозможен. Частицы способные переносить электрические заряды существуют не во всех веществах, те в которых они есть, называются проводниками и полупроводниками. А вещества, в которых таких частиц нет – диэлектриками.
Принято считать направление тока от плюса к минусу, при этом электроны движутся от минуса к плюсу!
Единица измерения силы тока – Ампер (А). В формулах и расчетах сила тока обозначается буквой I. Ток в 1 Ампер образуется при прохождении через точку электрической цепи заряда в 1 Кулон (6,241·1018 электронов) за 1 секунду.
Вновь обратимся к нашей аналогии вода – электричество. Только теперь возьмем два резервуара и наполним их равным количеством воды. Отличие между баками в диаметре выходной трубы.
Откроем краны и убедимся, что поток воды из левого бака больше (диаметр трубы больше), чем из правого. Такой опыт – явное доказательство зависимости скорости потока от диаметра трубы. Теперь попробуем уравнять два потока. Для этого добавим в правый бак воды (заряд). Это даст большее давление (напряжение) и увеличит скорость потока (ток). В электрической цепи в роли диаметра трубы выступает сопротивление.
Проведенные эксперименты наглядно демонстрируют взаимосвязь между напряжением, током и сопротивлением. Подробнее о сопротивлении поговорим чуть позже, а сейчас еще несколько слов о свойствах электрического тока.
Если напряжение не меняет свою полярность, плюс на минус, и ток течет в одном направлении, то – это постоянный ток и соответственно постоянное напряжение. Если источник напряжения меняет свою полярность и ток течет то в одном направлении, то в другом – это уже переменный ток и переменное напряжение. Максимальные и минимальные значения (на графике обозначены как Io) – это амплитудные или пиковые значения силы тока. В домашних розетках напряжение меняет свою полярность 50 раз в секунду, т.е. ток колеблется то туда, то сюда, получается, что частота этих колебаний составляет 50 Герц или сокращенно 50 Гц. В некоторых странах, например в США принята частота 60 Гц.
Сопротивление
Электрическое сопротивление – физическая величина, определяющая свойство проводника препятствовать (сопротивляться) прохождению тока. Единица измерения сопротивления – Ом (обозначается Ом или греческой буквой омега Ω). В формулах и расчетах сопротивление обозначается буквой R. Сопротивлением в 1 Ом обладает проводник к полюсам которого приложено напряжение 1 В и протекает ток 1 А.
Проводники по-разному проводят ток. Их проводимость зависит, в первую очередь, от материала проводника, а также от сечения и длины. Чем больше сечение, тем выше проводимость, но, чем больше длина, тем проводимость ниже. Сопротивление – это обратное понятие проводимости.
На примере водопроводной модели сопротивление можно представить как диаметр трубы. Чем он меньше, тем хуже проводимость и выше сопротивление.
Сопротивление проводника проявляется, например, в нагреве проводника при протекании в нем тока. Причем, чем больше ток и меньше сечение проводника – тем сильнее нагрев.
Мощность
Электрическая мощность – это физическая величина, определяющая скорость преобразования электроэнергии. Например, вы не раз слышали: «лампочка на столько-то ватт». Это и есть мощность потребляемая лампочкой за единицу времени во время работы, т.е. преобразовании одного вида энергии в другой с некоторой скоростью.
Источники электроэнергии, например генераторы, также характеризуется мощностью, но уже вырабатываемой в единицу времени.
Единица измерения мощности – Ватт (обозначается Вт или W). В формулах и расчетах мощность обозначается буквой P. Для цепей переменного тока применяется термин Полная мощность, единица измерения – Вольт-ампер (В·А или V·A), обозначается буквой S.
И в завершение про Электрическую цепь. Данная цепь представляет собой некоторый набор электрических компонентов, способных проводить электрический ток и соединенных между собой соответствующим образом.
Что мы видим на этом изображении – элементарный электроприбор (фонарик). Под действием напряжения U (В) источника электроэнергии (батарейки) по проводникам и другим компонентам обладающих разными сопротивлениями R (Ом) от плюса к минусу течет электрический ток I (А) заставляющий светиться лампочку мощностью P (Вт). Не обращайте внимания на яркость лампы, это из-за плохого давления и малого потока воды батареек.
Фонарик, что представлен на фотографии, собран на базе конструктора «Знаток». Данный конструктор позволяет ребенку в игровой форме познать основы электроники и принцип работы электронных компонентов. Поставляется в виде наборов с разным количеством схем и разного уровня сложности.
мощность постоянного тока
Немного о мощности постоянного тока. Не надо долго ходить за примерами и что-то объяснять в том плане, что механическая работа, которую совершает двигатель, выделяемая нагревателем теплота вполне измеримы. От каких же величин зависит совершаемая работа?
Чем дольше потребители тока, будь то лампы или двигатель, включены, тем больше электроэнергии потребляется. И тем больше количество произведенной работы. Но и при простом увеличении количества потребителей сила тока увеличивается, поскольку обычно они включаются параллельно. Следовательно, произведенная электрическая работа возрастает с увеличением силы тока и времени. Но влияет еще и третья величина. Две параллельно включенные лампы потребляют двойную энергию по сравнению с одной. А, значит, и двойной ток. Тот же результат получим, если соединим две лампы последовательно и подадим двойное напряжение (см. рис.1).
Электрическая работа зависит, следовательно, и от напряжения. Поэтому для работы электрического тока в течение отрезка времени получим зависимость:
W=UIt
Здесь U — напряжение, I — сила тока, t — время, W — количество произведенной работы. Теперь о самой мощности. Под мощностью понимают работу, совершаемую за определенное время. Таким образом, P=W/t. Если теперь вместо W подставить выражение для электрической работы, то
P=UIt/t=UI
Таким образом, мощность — это произведение напряжения на силу тока. Единицей мощности служит 1Вт, в честь ее открывателя, шотландского инженера, Джеймса Уайта (1736 — 1819).
Вернувшись назад к формуле
работы тока W=UIt увидим, что это произведение электрической мощности P=UI и времени t, в течение которого эта мощность действует. Если время выразить в часах, то плучим количество потребленной энергии «ватт-час». Такая единица измерения является маленькой, поэтому пользуются «киловатт-часом». 1кВтч=1000Втч
Кстати, кто еще далек от электричества, есть «хитрый» перерасчет электрической мощности в механическую:
1кВтч=367000кгс*м; 1кВт=102кгс*м/с
Constant-Current — Электрический ток в физике
Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.
Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.
Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,
где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.
Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим
Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:
Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле
По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.
Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как
Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:
Затраченная же работа источника тока равна работе сторонних сил:
где .
Тогда .
КПД источника , где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.
Рис. 1
Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж.
1 Дж = Кл·В = А·В·с.
Измеряют работу электрического тока счетчиками.
Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле или P = IU.
Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока: . В этом случае речь идет о тепловой мощности.
Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.
Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.
Для измерения мощности тока существуют специальные приборы — ваттметры.
формулы и порядок расчета при разных известных показателях
Сила тока — это движение заряженных частиц, являющееся одной из ключевых характеристик в цепи электричества. Данная величина измеряется Амперами. Силой электрического тока измеряется нагрузка на проводящих ток проводах, шинах и дорожках плат.
Благодаря этой величине можно понять, сколько энергии протекает в проводнике за определённое количество времени. Вычислить значение можно разными способами, которые зависят от имеющихся в наличии данных.
Из-за того, что варианты решения и известные значения могут быть разными, можно встретиться с проблемами в расчетах. Далее рассмотрим, как правильно можно определить силу тока с помощью разных значений.
С помощью мощности и напряжения
В случае если из всех известных данных у вас есть только значение мощности потребления и напряжение, нужно воспользоваться простой формулой, не включающей в себя сопротивление: P = IU
При этом из этой же формулы можно получить следующую: I = P/U
Данная формула подходит для цепи с постоянным током. А для расчетов силы тока в цепях с переменным током (такая формула может понадобиться Вам, если Вы хотите вычислить силу тока в электрическом двигателе) нужно учитывать ещё и коэффициент мощности (его же иначе называют «косинус фи»).
В этом случае для электродвигателя с тремя фазами действует нужно построить расчет немного иначе.
Найдите P, учитывая при этом коэффициент полезного действия: Р1 = Р2/η
В этой формуле P 2 является активной полезной мощностью на вале, а η является коэффициентом полезного действия. Эти значения обычно можно найти на самом двигателе.
После этого нужно найти полную мощность с учётом коэффициента мощности (он же cos φ, его значение указано на двигателе): S = P1/cosφ
Далее определите ток потребления: Iном = S/(1,73·U)
1.73 является корнем из трёх, это значение нужно для расчёта цепи на три фазы. Значение напряжение будет зависеть от способа включения электродвигателя (треугольником или звездой) и Вольт, чаще всего встречается 380.
С помощью напряжения или мощности и сопротивления
Бывает и так, что для расчета силы электрического тока нужно задействовать напряжение с определённого участка или величину нагрузки. Тогда проще всего применить закон Ома, который знает каждый, кто немного разбирается в физике.
Если же напряжение Вам неизвестно, но вы знаете значение мощности и сопротивления, проводите расчет по следующей формуле: P=UI
Снова применяя закон Ома, можно получить следующее: U=IR
В таком случае: P=I2*R
Получаем следующую формулу: I2=P/R
Кроме того, можно применить следующий расчет, исходя из этих же формул и значений: I=(P/R)1/2
С помощью электродвижущей силы, внутреннего сопротивления и нагрузки
В некоторых студенческих учебниках встречаются так называемые задачки с подвохом. К ним относятся и те, где есть электродвижущая сила и значение внутреннего сопротивления.
Вспоминая закон Ома, силу электрического тока можно получить следующим образом: I=E/(R+r)
Здесь Е будет электродвижущей силой, а r будет внутренним сопротивлением. R представляет собой нагрузку.
С помощью закона Джоуля-Ленца
Некоторые затрудняются определять силу тока, если есть:
- Время;
- Значение сопротивления;
- Кол-во выделяемого тепла от проводника.
С помощью решения задачи, нужно воспользоваться законом Джоуля-Ленца: Q=I2Rt
Исходя из этой формулы, расчет нужно построить так: I2=QRt
Либо так: I=(Q/Rt)1/2
Практические примеры
Чтобы правильно понять все приведённые выше формулы, предлагаем Вам рассмотреть несколько примеров, которые могут встретиться в учебниках по физике.
Первый пример: рассчитаем силу тока из 2-х резисторов, при этом в цели есть последовательное и параллельное соединение. В источнике питания двенадцать Вольт.
Исходя из условий задачи, нужно получить два значения: одно для последовательного, а другое для параллельного соединения.
Для получения значения последовательного соединения, нужно сложить сопротивления, чтобы вывести общее: R1+R2=1+2=3 Ома
Далее определить силу тока можно через закон Ома: I=U/R=12/3=4 Ампера
Для параллельного соединения расчёт будет следующим: Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
С применением закона Ома результат будет таким: I=12*0,67=18А
Второй пример: нужно найти ток при соединении разных элементов цепи. На выход питание составляет 24 Вольта, на резисторы от первого к третьему 1, 2 и 3 Ома соответственно.
В этом случае воспользовавшись формулой, которую мы определили выше, видим следующий расчет: Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
С этой формулой схема будет выглядеть так:
Теперь определяем силу тока: I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Это все способы определения силы. Потренируйтесь использовать эти расчеты для типовых задач, и Вы сможете лучше понять принцип вычисления силы тока в электрической цепи!
Что такое электроэнергия (P)
Электрическая мощность — это норма потребления энергии в электрическом
схема.
Электрическая мощность измеряется в ваттах.
Определение электроэнергии
Электрическая мощность P равна потребляемой энергии E, разделенной
по времени расхода t:
P — электрическая мощность в ваттах (Вт).
E — потребление энергии в джоулях (Дж).
t — время в секундах (с).
Пример
Найдите электрическую мощность электрической цепи, потребляющей
120 джоулей за 20 секунд.
Решение:
E = 120 Дж
т = 20 с
P = E / т = 120 Дж / 20 с = 6 Вт
Расчет электроэнергии
P = В ⋅ I
или
P = I 2 ⋅ R
или
P = V 2 / R
P — электрическая мощность в ваттах (Вт).
В — это напряжение в вольтах (В).
I — ток в амперах (А).
R — сопротивление в Ом (Ом).
Мощность цепей переменного тока
Формулы для однофазного переменного тока.
Для трехфазного переменного тока:
Когда линейное напряжение (В L-L )
используется в формуле, умножьте однофазную мощность на квадрат
корень из 3 (√3 = 1,73).
При нулевом напряжении (В L-0 )
используется в формуле, умножьте однофазную мощность на 3.
Реальная мощность
Реальная или истинная мощность — это мощность, которая используется для работы на
Загрузка.
P = В СКЗ I СКЗ cos
φ
P — реальная мощность в ваттах.
[Вт]
В действующее значение — среднеквадратичное значение напряжения = В пиковое значение / √2
в вольтах [В]
I rms — среднеквадратичное значение тока = I пиковое / √2
в амперах [A]
φ — это фазовый угол импеданса = разность фаз
между напряжением и током.
Реактивная мощность
Реактивная мощность — это мощность, которая тратится впустую и не используется для
работать под нагрузкой.
Q = В СКЗ I СКЗ
sin φ
Q — реактивная мощность в
вольт-ампер-реактивная [VAR]
В действующее значение — среднеквадратичное значение напряжения = В пиковое значение / √2
в вольтах [В]
I rms — среднеквадратичное значение тока = I пиковое / √2
в амперах [A]
φ — это фазовый угол импеданса = разность фаз
между напряжением и током.
Полная мощность
Полная мощность — это мощность, подаваемая в цепь.
S = В СКЗ I СКЗ
S — полная мощность в
Вольт-ампер [ВА]
В действующее значение — среднеквадратичное значение напряжения = В пиковое значение / √2
в вольтах [В]
I rms — среднеквадратичное значение тока = I пиковое / √2
в амперах [A]
Соотношение активной / реактивной / полной мощностей
Активная мощность P и реактивная мощность Q вместе дают кажущуюся мощность.
мощность S:
P 2 + Q 2 = S 2
P — реальная мощность в ваттах.
[Вт]
Q — реактивная мощность в
вольт-ампер-реактивная [VAR]
S — полная мощность в
Вольт-ампер [ВА]
Коэффициент мощности ►
См. Также
15.5: Питание в цепи переменного тока
Цели обучения
К концу раздела вы сможете:
- Опишите, как можно записать среднюю мощность от цепи переменного тока в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения
- Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с \ (P = IV \), где I — ток через элемент, а \ (V \) — напряжение на нем.Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность \ (p (t) = i (t) v (t) \) также зависит от времени. График \ (p (t) \) для различных элементов схемы показан на рисунке \ (\ PageIndex {1} \). Для резистора \ (i (t) \) и \ (v (t) \) синфазны и, следовательно, всегда имеют один и тот же знак. Для конденсатора или катушки индуктивности относительные знаки \ (i (t) \) и \ (v (t) \) меняются в течение цикла из-за разницы фаз. Следовательно, \ (p (t) \) в одни моменты времени положительно, а в другие — отрицательно, что указывает на то, что емкостные и индуктивные элементы вырабатывают энергию в одни моменты и поглощают ее в другие.
Рисунок \ (\ PageIndex {1} \): График мгновенной мощности для различных элементов схемы. (a) Для резистора \ (P_ {ave} = I_0V_0 / 2 \), тогда как для (b) конденсатора и (c) катушки индуктивности \ (P_ {ave} = 0 \). (d) Для источника \ (P_ {ave} = I_0V_0 (cos \, \ phi) / 2 \), который может быть положительным, отрицательным или нулевым, в зависимости от \ (\ phi \).
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью .T \ sin \ omega t \, \ cos \, \ omega t \, dt = 0. \ nonumber \]
Следовательно, средняя мощность, связанная с элементом схемы, равна
\ [\ boxed {P _ {\ mathrm {ave}} = \ frac {1} {2} I_ {0} V_ {0} \ cos \ phi.} \ Label {eq5} \]
В инженерных приложениях \ (\ cos \ phi \) известен как коэффициент мощности , который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за отсутствия напряжения и тока. фазы.{2} R. \ label {eq10} \]
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения. Оба уравнения \ ref {eq5} и \ ref {eq10} верны для средней мощности, но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна \ (110 \ sqrt {2} \, V = 156 \, V \).Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, установленный на бытовой розетке, будет показывать 110 В.
Для конденсатора и катушки индуктивности \ (\ phi = \ pi / 2 \) и \ (- \ pi / 2 \, rad \), соответственно. Поскольку \ (\ cos \, \ pi / 2 = cos (- \ pi / 2) = 0 \), мы находим из уравнения \ ref {eq5}, что средняя мощность, рассеиваемая любым из этих элементов, равна \ (P_ {ave } = 0 \). Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода.Это поведение проиллюстрировано на графиках на рисунках \ (\ PageIndex {1b} \) и \ (\ PageIndex {1c} \), которые показывают, что \ (p (t) \) колеблется синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение. Если \ (cos \, \ phi> 0 \), генератор вырабатывает энергию; если \ (cos \, \ phi <0 \), он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
.
\ [P_ {ave} = I_ {rms} V_ {rms} \, \ cos \, \ phi. \]
Для генератора в цепи RLC ,
\ [tan \, \ phi = \ dfrac {X_L — X_C} {R} \] и
\ [cos \, \ phi = \ dfrac {R} {\ sqrt {R ^ 2 + (X_L — X_C) ^ 2}} = \ dfrac {R} {Z}.{-6} F \) и \ (R = 5.00 \, \ Omega \).
- Какое среднеквадратичное напряжение на генераторе?
- Какое сопротивление цепи?
- Какова средняя выходная мощность генератора?
Стратегия
Действующее значение напряжения — это амплитуда напряжения, умноженная на \ (1 / \ sqrt {2} \). Импеданс цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по формуле \ ref {eq30}, потому что у нас есть полное сопротивление цепи \ (Z \), среднеквадратичное напряжение \ (V_ {rms} \) и сопротивление \ (R \).2 / R \), где В заменяет действующее напряжение.
Упражнение \ (\ PageIndex {1A} \)
Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
- Ответ
\ (v (t) = (10.0 \, V) \, \ sin \, 90 \ pi t \)
Упражнение \ (\ PageIndex {1B} \)
Покажите, что среднеквадратичные значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток равен \ (I_ {rms} \), выражаются как \ (I_ {rms} R, \, I_ {rms} X_C \) и \ (I_ {rms} X_L \) соответственно.Определите эти значения для компонентов цепи RLC по формуле \ ref {eq5}.
- Ответ
2,00 В; 10,01 В; 8.01 В
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (by 4.0).
Согласно закону Ома, I ∝ V, но I ∝ 1 / V в уравнении мощности. Как?
In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?
Это еще один непонятный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.
Согласно закону Ома, Ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как объяснить?
т.е.
- Согласно закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
- Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)
Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.
Давайте проясним путаницу, связанную с утверждением.
P = V x I
Фактически, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной или она меняется.
- Если мощность источника постоянна, ток будет уменьшаться при увеличении напряжения.
- Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при увеличении напряжения, поскольку мощность перестает быть постоянной i.е. мощность также была увеличена.
В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).
В = I x R
По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.
Согласно формуле мощности, в ней говорится, что ток обратно пропорционален напряжению, если мощность остается прежней.
Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение мощность). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.
То же самое и с генерирующей станцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.
Вкратце:
- Если мощность постоянна = Напряжение обратно пропорционально току то есть В 1 / I в P = VxI .
- Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , то есть В V I в В = IxR .
Это точная причина, по которой по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.
Связанные вопросы / ответы:
Формулы для расчета коэффициента мощности — RF Cafe
Коэффициент мощности измеряет фазовый угол между мгновенным напряжением и мгновенным током в цепи.
Напряжение ( E ) опережает ток ( I ) на 90 ° по индуктивной ( L ) цепи
и напряжение ( E ) отстает от тока ( I ) на 90 ° в емкостной ( C ) цепи.
Популярным мнемоником является ELI человек ICE , так как E ведет (идет впереди) I в
ELI, а E отстает (идет после) I в ICE.
| коэффициент мощности (P f ) = cos (q) | |
| Полная мощность (P) = I * В | |
| Истинная мощность = P | |
| I = Текущий | |
| q = фазовый угол | |
| В = Напряжение |
| Формулы мощности | ||||
| Полная мощность P = I * V P = I 2 * R P = V 2 / R | Истинная мощность P = I * V * cos (q) P = I 2 * Z * cos (q) P = V 2 * cos (q) / Z P = P a * P f | Импеданс Z = V 2 * cos (q) / P Z = P / [I 2 * cos (q)] | ||
| Ток I = P / [V * cos (q)] I = sqrt {P / [Z * cos (q)]} | Напряжение В = P / [I * cos (q)] В = sqrt [P * Z / cos (q)] | |||
| ||||
Зависимость тока от напряжения — разница и сравнение
Взаимосвязь между напряжением и током
Ток и напряжение — две фундаментальные величины в электричестве.Напряжение — это причина, а ток — это следствие.
Напряжение между двумя точками равно разности электрических потенциалов между этими точками. На самом деле это электродвижущая сила (ЭДС), ответственная за движение электронов (электрический ток) по цепи. Поток электронов, приводимый в движение напряжением, называется током. Напряжение представляет собой потенциал каждого кулоновского электрического заряда для выполнения работы.
В следующем видео объясняется взаимосвязь между напряжением и током:
Схема
Электрическая цепь с источником напряжения (эл.грамм. аккумулятор) и резистор.
Источник напряжения имеет две точки с разностью электрических потенциалов. Когда между этими двумя точками существует замкнутый контур, он называется цепью, и ток может течь. При отсутствии цепи ток не будет течь, даже если есть напряжение.
Условные обозначения и единицы
Заглавная курсивная буква I обозначает ток. Стандартная единица измерения — Ампер (или Ампер), обозначаемая буквой A. Единица измерения тока в системе СИ — кулонов в секунду .
1 ампер = 1 кулон в секунду.
Один ампер тока соответствует одному кулону электрического заряда (6,24 x 10 18 носителей заряда), проходящего мимо определенной точки в цепи за одну секунду. Устройство, используемое для измерения тока, называется Амперметр .
Заглавная курсивная буква В обозначает напряжение.
1 вольт = 1 джоуль / кулон.
Один вольт перемещает один кулон (6,24 x 10 18 ) носителей заряда, например электронов, через сопротивление в 1 Ом за одну секунду.Вольтметр используется для измерения напряжения.
Поля и интенсивность
Электрический ток всегда создает магнитное поле. Чем сильнее ток, тем сильнее магнитное поле.
Напряжение создает электростатическое поле. По мере увеличения напряжения между двумя точками электростатическое поле становится более интенсивным. По мере увеличения расстояния между двумя точками, имеющими заданное напряжение по отношению друг к другу, интенсивность электростатического заряда между точками уменьшается.
Последовательные и параллельные соединения
В последовательной цепи
Напряжения суммируются для компонентов, соединенных последовательно. Токи одинаковы во всех последовательно соединенных компонентах.
Электрические компоненты в последовательном соединении
Например, если батарея 2 В и батарея 6 В подключены последовательно к резистору и светодиоду, ток через все компоненты будет одинаковым (скажем, 15 мА), но напряжения будут разными (5 В на резисторе и 3 В на светодиод).Эти напряжения складываются с напряжением батареи: 2 В + 6 В = 5 В + 3 В.
В параллельной цепи
Сумма токов для компонентов, соединенных параллельно. Напряжения одинаковы на всех компонентах, подключенных параллельно.
Электрические компоненты при параллельном подключении
Например, если одни и те же батареи подключены к резистору и светодиоду параллельно, напряжение через компоненты будет одинаковым (8 В). Однако ток 40 мА через аккумулятор распределяется по двум путям в цепи и прерывается до 15 мА и 25 мА.
Список литературы
Мгновенная, средняя, активная и реактивная мощность
Вперед
В нескольких последних статьях мы обсудили и разработали некоторые важные концепции линий электропередачи. В прошлый раз мы говорили о протяженных линиях электропередачи. Здесь мы обсуждаем простую, но важную базовую концепцию «Электроэнергия».Это освежит наши знания, прежде чем мы двинемся дальше.
Электроэнергия имеет то же значение, что и механическая сила, но здесь сила или энергия, которые нас интересуют, находятся в электрической форме. Мы часто сталкиваемся с такими терминами, как мгновенная, средняя, полная, действительная, реактивная, полная и комплексная мощность или просто мощность. Что они имеют в виду? как они связаны? Об этом мы поговорим здесь и в следующей статье.
Цепь постоянного тока
Пока наш анализ ограничивается цепью постоянного тока (DC), мощность, потребляемая резистивной нагрузкой, является произведением напряжения на сопротивлении и тока, протекающего через сопротивление. Это действительно просто.
P = V. я
Мощность, потребляемая нагрузкой, является произведением напряжения на нагрузке и тока, потребляемого нагрузкой (рис. A).Или мощность, подаваемая источником постоянного тока (батарея / элемент), является произведением напряжения на элементе и тока, подаваемого элементом. На рисунке в нашем примере они равны (с учетом идеальной батареи с нулевым внутренним сопротивлением). Закон сохранения энергии подразумевает, что мощность, подаваемая источником, должна быть такой же, как мощность, потребляемая цепью. В случае цепи постоянного тока мгновенная мощность равна средней мощности.
Цепь переменного тока
Что это за мощность, о которой мы говорим при анализе цепей переменного тока.Основная проблема заключается в том, что переменное напряжение и ток синусоидально изменяются со временем. Кроме того, наличие в цепи реактивных элементов, таких как индуктор и конденсатор, сдвигает волну тока относительно волны напряжения (угла сдвига фаз).
Мощность — это скорость, с которой энергия потребляется нагрузкой или вырабатывается генератором. Будь то цепь постоянного или переменного тока, значение мгновенной мощности получается путем умножения мгновенного напряжения на мгновенный ток.Если в любой момент времени t значения напряжения и тока представлены синусоидальными функциями как
v = V m sin ωt
i = I м sin (ωt-φ)
V m и I m — максимальные значения синусоидального напряжения и тока.Здесь ω = 2 π f
f — частота, а ω — угловая частота вращающихся векторов напряжения или тока. Должно быть понятно, что для энергосистемы f обычно составляет 50 или 60 Гц
φ — разность фаз между напряжением и током.
Как мы уже говорили, мгновенная мощность — это произведение мгновенного напряжения и тока, если мы назовем мгновенную мощность как p, то
p = v.i = V м sin ωt . I m sin (ωt-φ)
или p = V m I m sin ωt sin (ωt-φ)
Применяя тригонометрическую формулу 2.sin A.sin B = cos (AB) — cos (A + B) получаем
Его можно записать как
Это уравнение мгновенной мощности
. На фиг.8-C нарисованы все три волны, соответствующие v, i и p. Графически мы также можем получить значение мгновенной мощности (p) в любой момент времени t, просто умножив значение тока i и напряжения v в этот конкретный момент t.(Вы можете проверить, что на диаграмме p отрицательно, когда либо v, либо i отрицательно, в противном случае p положительно. См. Точки, где p равно нулю). На графике мы показали горизонтальную ось как угол φ вместо времени t для облегчения визуализации. Должно быть ясно, что оба варианта верны.
Ясно, что мгновенная мощность p состоит из двух членов. Первый член постоянен, потому что для данной нагрузки фазовый угол φ фиксирован.Он не изменится, если не изменится нагрузка. Второй член изменяется во времени синусоидально из-за наличия члена cos (2ωt-φ). Обратите внимание, что мгновенная частота сети в два раза больше частоты напряжения или тока, поэтому мгновенная мощность в однофазной цепи изменяется синусоидально.
Мгновенная мощность, p = постоянный член + синусоидальный колебательный член.
За один полный период среднее значение колеблющегося члена равно нулю.
Тогда какова средняя мощность в заданное время, скажем, за один период времени волны?
Это постоянный член.
Вот еще один способ подумать о средней мощности.
Просто заметьте, что мгновенная мощность на короткое время отрицательна.Для любого временного интервала вы просто найдете общую + ve площадь A + (над горизонтальной осью (синяя линия) и под кривой p) и общую площадь -ve A- (под горизонтальной осью и над кривой p). Чистая площадь получается вычитанием A- из A +. Разделив эту чистую площадь (на интервал времени T и , мы получим среднюю мощность (P). Вы можете сделать это с помощью расчетов. В конечном итоге вы получите только первый член в приведенной выше формуле для мгновенной мощности p.
Еще одним способом легче понять, что формула для мгновенной мощности p имеет постоянный член (V m .I m /2) cos φ и другой синусоидальный член (V m . I m /2) cos (2 wt — φ). Фактически p — это колебательная мощность, которая колеблется около среднего постоянного члена (V m .I m /2) cos φ.
Так что средняя мощность
Вышеуказанная формула может быть записана как
здесь,
V и I являются векторным представлением среднеквадратичных значений * синусоид напряжения и тока.Символы | V | и | I | — величины векторов V и I. (См. определение RMS-значения внизу).
Эта формула выше — ваша любимая формула полезной мощности, которая нас больше всего беспокоит. Эта формула средней мощности используется для определения мощности, потребляемой нагрузкой. Ежемесячный счет за электроэнергию дома основан на этой мощности. Инженеры и техники в энергетике или электротехнике просто используют термин мощность вместо средней мощности. Поэтому всякий раз, когда мы просто называем мощность, это означает среднюю мощность.
Конечно, мгновенная мощность колеблется по своей природе. Как мы уже говорили, он колеблется не вокруг горизонтальной оси, а вокруг средней мощности P (голубая горизонтальная линия).
P будет равно нулю, когда cos φ = 0 или φ = 90 градусов, то есть когда фазовый угол между волнами напряжения и тока составляет 90 градусов.Это только тогда, когда нагрузка чисто индуктивная или емкостная. В этом случае второй член остается только в формуле мгновенной мощности.
Из приведенного выше рисунка в течение некоторого времени мощность становится отрицательной, что означает, что нагрузка подает энергию к источнику за этот период. Это связано с наличием в нагрузке реактивного элемента.
Приведенную выше формулу для мгновенной мощности можно записать в другой форме. Эта форма на самом деле является попыткой отличить колеблющуюся реактивную мощность от формулы мгновенной мощности.Переставляя члены в уравнении для мгновенной мощности выше, мы получаем
p = | V | | Я | cos φ (1-cow2ωt) — | V | | Я | sin φ sin2ωt
В этом уравнении первый член | V | | Я | cos φ (1-cow2ωt) — колебательный, среднее значение которого | V | | Я | cos φ. Об этой средней мощности мы уже говорили.
Второй член | V | | Я | sin φ sin2ωt, который также является колебательным, но с нулевым средним значением. Максимальное значение этого члена составляет | V | | Я | грех φ. Это так называемая реактивная мощность.Таким образом, реактивная мощность — это максимальное значение колебательной мощности, которая многократно отбирается от источника и снова возвращается к источнику в течение каждого цикла. Таким образом, среднее значение этой реактивной мощности равно нулю.
Средняя мощность P называется реальной мощностью. Иногда ее еще называют активной мощностью.
Активная мощность = P = | V | | Я | cos φ
Обычно записывается как P = VI cos φ. Но следует помнить, что V и I — это среднеквадратичные значения напряжения и тока. Например, когда мы говорим однофазный 220 вольт переменного тока, это означает, что действующее значение напряжения составляет 220 вольт (это не максимальное значение синусоиды напряжения)
Реактивная мощность = Q = | V | | Я | sin φ
Реальная мощность измеряется в ваттах, а реактивная мощность — в вар (вольт-ампер-реактивность).В энергетическом секторе эти блоки слишком малы, поэтому реальная мощность измеряется в мегаваттах (МВт), а реактивная мощность — в мегаварах (МВАр). Буква R в конце обозначает реактивную мощность.
Часто студенты и практикующие инженеры не понимают средней мощности (часто просто называемой мощностью). Они думают, что умножая действующее значение напряжения на среднеквадратичный ток, они получают среднеквадратичную мощность. Нет, это неправильно. Нет мощности RMS. Среднеквадратичная мощность не имеет значения или не определена. (Также см. Определение значения RMS ниже в конце).Это средняя мощность, или реальная мощность, или истинная мощность.
Трехфазная сбалансированная система с питанием
Рассмотрим трехфазную сбалансированную систему. Трехфазная сбалансированная система анализируется с учетом только одной фазы и нейтрали. Это называется поэтапным анализом. Таким образом, приведенный выше анализ для одной фазы верен для сбалансированного трехфазного случая. Пусть суммарная мощность здесь P . Тогда мы получаем общую трехфазную мощность как трижды по сравнению с однофазным случаем.
P t = 3 | V | | Я | cos φ
Следует помнить, что | V | и | Я | — значения для каждой фазы.и φ — фазовый угол нагрузки в пофазном анализе.
Приведенная выше формула для сбалансированной трехфазной системы может быть записана как
P t = √3 | V l | | I l | cos φ
В приведенной выше формуле V l и I l являются линейным напряжением и током (Рис-D).Это уравнение не зависит от типа подключения трехфазной нагрузки, т. Е. Нагрузки, подключенной по схеме треугольник или звезда. Вы должны знать линейное напряжение, линейный ток и фазовый угол φ, как указано выше. Эта форма очень удобна и часто используется при расчете мощности.
Есть одно основное различие между однофазной и полной трехфазной мощностью. Мгновенная однофазная мощность пульсирует.В сбалансированном трехфазном случае мгновенная мощность каждой фазы пульсирует, но три пульсирующие волны мощности смещены друг от друга на 120 градусов. В любой момент времени сумма этих трех мгновенных волн мощности является постоянной величиной 3 | V | | Я | cos φ. Таким образом, общая мощность, потребляемая в трехфазной сбалансированной системе, не пульсирует. Непульсирующая мощность также подразумевает желаемый непульсирующий крутящий момент в случае трехфазных вращающихся машин. В больших трехфазных двигателях это действительно необходимо.
* Среднеквадратичное значение синусоид переменного тока
Значение переменного напряжения или тока, которое вызывает такой же нагрев (или такую же энергию), который вырабатывается, если вместо переменного тока применяется постоянное напряжение или ток, численно равные среднеквадратичному значению переменного тока. Эта концепция помогает сделать формулы мощности похожими для цепей постоянного и переменного тока.
Вам следует прочитать следующую статью о Треугольнике степеней и Комплексной мощности.
Закон
Ома и электрическая мощность
Для анализа цепей постоянного тока обычно используются различные методы, такие как закон Ома, сетевые теоремы и другие инструменты для упрощения цепей.Анализ цепи постоянного тока выполняется в основном для определения неизвестных величин, таких как напряжение, ток, сопротивление и мощность, которые связаны с одним или несколькими элементами электронной схемы. В качестве основного закона для упрощения схем закон Ома определяет линейную зависимость между напряжением, током и сопротивлением. Расскажите подробнее о законе Ома.
Закон Ома
Это основной, важнейший и важный закон, исследующий взаимосвязь между напряжением, током и сопротивлением в электрической цепи.В нем говорится, что при постоянной температуре ток, протекающий по цепи, прямо пропорционален напряжению или разности потенциалов в этой цепи.
В алгебраической форме V∝ I
V = IR
Где
I — ток, протекающий по цепи и измеренный в амперах
В — это напряжение, приложенное к цепи и измеренное в вольтах
R — константа пропорциональности, называемая сопротивлением, которая измеряется в Ом.
Это сопротивление также указывается в килоомах, мегаомах и т. Д.
Следовательно, закон Ома гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в этой цепи. Закон Ома может применяться к отдельным частям или ко всей цепи.
Математически, ток, I = V / R
Напряжение, V = IR
Сопротивление, R = V / I
Вернуться к началу
Треугольник закона Ома
Схема ниже показывает взаимосвязь между различными величинами в законе Ома , называется треугольником закона Ома.Это простой метод описания, а также легко запомнить соотношение между напряжением, током и сопротивлением.
На рисунке выше показан треугольник закона Ома, где отдельные термины, такие как напряжение, ток и сопротивление, и их формулы представлены из основного уравнения закона Ома. На приведенном выше рисунке один параметр рассчитывается из двух оставшихся параметров. Таким образом, можно сделать вывод, что, когда сопротивление велико, ток будет низким, а ток будет большим, когда сопротивление низкое для любого приложенного напряжения.
Вернуться к началу
Электроэнергия
Электроэнергия показывает скорость, с которой энергия передается по цепи. Электрическая мощность измеряется в ваттах. Эта мощность потребляется, когда напряжение вызывает протекание тока в цепи.
Следовательно, электроэнергия является произведением напряжения и тока.
Математически, P = VI
Из закона Ома, V = IR и I = V / R
Подставляем в уравнение мощности
P = I 2 R
P = V 2 / R
Следовательно, электрическая мощность, P = VI или I 2 R или V 2 / R
Это три основные формулы для определения электрической мощности в цепи.Таким образом, мощность может быть рассчитана, если известна любая из двух величин.
В начало
Треугольник мощности
Подобно треугольнику закона Ома, на рисунке ниже показан треугольник мощности, показывающий соотношение между мощностью, напряжением и током. Этот рисунок легко запоминает уравнения отдельных параметров. Округлите и скройте параметр, который должен быть измерен, а положение оставшихся двух параметров дает уравнение для поиска скрытого или округленного параметра, как показано на рисунке ниже.
Вернуться к началу
Круговая диаграмма закона Ома
Помимо вышеперечисленных двух концепций, существует еще один метод определения параметров цепи с использованием закона Ома, который представляет собой круговую диаграмму закона Ома. Используя круговую диаграмму закона Ома, можно легко запомнить все уравнения, чтобы найти напряжение, ток, сопротивление и мощность, которые необходимы для упрощения электрических цепей, которые могут быть простыми или сложными.
На рисунке выше показана круговая диаграмма, которая показывает взаимосвязь между мощностью, напряжением, током и сопротивлением.Эта диаграмма разделена на четыре единицы мощности, напряжения, сопротивления и тока. Каждый блок состоит из трех формул с двумя известными значениями для каждой формулы. Из диаграммы для поиска каждого параметра в цепи мы можем использовать любую из трех доступных формул.
В начало
Графическое представление закона Ома
Для лучшего понимания этой концепции ниже представлена экспериментальная установка, где регулируемый источник напряжения с шестью ячейками (2 В каждая) подключен к нагрузочному резистору через переключатель напряжения. выключатель.Измерительные приборы, такие как вольтметр и амперметр, также подключаются к цепи для измерения напряжения и тока в цепи.
Регулируемый источник напряжения с нагрузочным резистором
Сначала подключите резистор 10 Ом и установите селекторный переключатель в положение один. Затем амперметр показывает 0,2 А, а вольтметр показывает 2 В, потому что I = V / R, то есть I = 2/10 = 0,2 А. Затем измените положение селекторного переключателя на вторую ячейку, чтобы подать 4 В на нагрузку и записать показания амперметра. По мере пошагового изменения селектора от первой позиции к последней мы получим текущие значения, такие как 0.2, 0,4, 0,6, 0,8, 1, 1,2 для значений напряжений 2, 4, 6, 8, 10 и 12 соответственно.
Аналогичным образом поместите резистор 20 Ом вместо резистора 10 Ом и проделайте ту же процедуру, что и выше. Мы получим значения тока 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 для значений напряжения 2, 4, 6, 8, 10 и 12 В соответственно. Постройте график этих значений, как показано ниже.
Графическое представление закона сопротивления
На приведенном выше графике для заданного напряжения ток меньше, когда сопротивление больше.Рассмотрим случай подачи напряжения 12 В, когда значение тока составляет 1,2 А, если сопротивление составляет 10 Ом, и 0,6 Ом, когда сопротивление составляет 20 Ом. Точно так же для того же потока тока напряжение тем выше, чем больше сопротивление. Исходя из приведенных выше результатов, отношение напряжения к току остается постоянным, когда сопротивление остается постоянным. Следовательно, зависимость между напряжением и током является линейной, и наклон этой линейной кривой становится тем круче, чем больше сопротивление.
В начало
Пример закона Ома
Рассмотрим схему ниже, в которой аккумулятор на 6 В подключается к нагрузке 6 Ом.Амперметр и вольтметры подключены к цепи для практического измерения силы тока и напряжения. Но используя закон Ома, мы можем найти ток и мощность следующим образом.
По закону Ома
V = IR
I = V / R
I = 6/6
I = 1 ампер
Мощность, P = VI
P = 6 × 1
P = 6 Вт
Но практически амперметр не показывает точное значение из-за внутреннего сопротивления батареи. Включая внутреннее сопротивление батареи (предположим, что внутреннее сопротивление батареи составляет 1 Ом), текущее значение рассчитывается следующим образом.
Общее сопротивление цепи 6 +1 = 7 Ом.
Ток, I = V / R
I = 6/7
I = 0,85 А
Наверх
Цепь фары в автомобиле
На рисунке ниже показана цепь фар в автомобиле без управления схема. Применяя закон Ома, мы можем определить ток, протекающий через каждый светильник. Обычно каждый фонарь подключается параллельно к батарее, что позволяет другим лампам гореть, даже если кто-то поврежден.К этим параллельным лампам подается батарея на 12 В, каждая из которых имеет сопротивление 2,4 (в данном случае рассматривается).
Общее сопротивление цепи R = R1x R2 / (R1 + R2), поскольку они включены параллельно.
R = 5,76 / 4,8 = 1,2
Тогда ток, протекающий по цепи, равен I = V / R
I = 12 / 1,2
I = 10A.
Ток, протекающий через отдельную лампу, равен I1 = I2 = 5 A (из-за того же сопротивления)
В начало
Закон Ома для цепей переменного тока
В общем, закон Ома может применяться и к цепям переменного тока.Если нагрузка индуктивная или емкостная, то также учитывается реактивное сопротивление нагрузки. Следовательно, с некоторыми изменениями закона сопротивления с учетом эффекта реактивного сопротивления, его можно применить к цепям переменного тока. Из-за индуктивности и емкости переменного тока между напряжением и током будет значительный фазовый угол. А также сопротивление переменного тока называется импедансом и представлено как Z.
Таким образом, закон сопротивления для цепей переменного тока задается как
E = IZ
I = E / Z
Z = E / I
Где E — напряжение в цепи переменного тока
I — ток, а
Z — полное сопротивление.
Все параметры в приведенном выше уравнении имеют сложную форму, которая включает фазовый угол. Подобно круговой диаграмме цепи постоянного тока, ниже представлена круговая диаграмма закона Ома для цепи переменного тока.
В начало
Пример закона Ома (цепи переменного тока)
Рассмотрим схему ниже, в которой нагрузка переменного тока (комбинация резистивной и индуктивной) подключается к источнику переменного тока 10 В, 60 Гц. Нагрузка имеет сопротивление 5 Ом и индуктивность 10 мГн.
Тогда значение полного сопротивления нагрузки, Z = R + jX L
Z = 5 + j (2∏ × f × L)
Z = 5+ j (2 × 3,14 × 60 × 10 × 10-3)
Z = 5 + j3,76 Ом или 6,26 Ом при фазовом угле -37,016
Ток, протекающий по цепи, равен
I = V / Z
= 10 / (5+ j3 .




 Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока.
Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока.