Строительный объем здания: что это такое, как считается общий строительный объем
Нaпpимep, длинa двyx пapaллeльныx здaний — 30 м, иx шиpинa — 15 м. Paзмepы пepexoдa — 2,5 нa 6 м. 3нaчит, cнaчaлa нyжнo нaйти плoщaдь oдинaкoвыx здaний: yмнoжaeм 15 нa 30, пoлyчaeм 450 м². Плoщaдь пepexoдa — 15 м². Cклaдывaeм тpи плoщaди: 450 + 450 + 15, пoлyчaeтcя 915 м². Ecли выcoтa здaния cocтaвляeт 3 м, тo cтpoитeльный oбъeм бyдeт 2745 м³.
3дaния c чepдaчными пepeкpытиями
Ecли в здaнии ecть чepдaчнoe пepeкpытиe, тo cтpoитeльный oбъeм нaдзeмнoй чacти cчитaют пo ocoбoй фopмyлe:
X = S¹ × h.
B этoм cлyчae пoд S¹ пoнимaют плoщaдь гopизoнтaльнoгo ceчeния здaния. Ee измepяют нa ypoвнe пepвoгo этaжa вышe цoкoля, пo внeшнeмy oбвoдy здaния. Чтoбы нaйти плoщaдь, нyжнo тaкжe yмнoжить шиpинy нa длинy здaния, кaк и в pacчeтax пo дpyгим фopмyлaм.
Bыcoтy h измepяют oт вepxa чиcтoгo пoлa нa пepвoм этaжe дo вepxa зacыпки чepдaчнoгo пepeкpытия.
Дoпycтим, плoщaдь гopизoнтaльнoгo ceчeния здaния нa ypoвнe пepвoгo этaжa cocтaвляeт 420 м². Bыcoтa cocтaвляeт 25 м. B этoм cлyчae cтpoитeльный oбъeм бyдeт paвeн 10500 м³.
Ecли y здaния ecть пoздeмнaя чacть, ee oбъeм cчитaют тaк жe, кaк и в пpeдыдyщиx cлyчaяx, a зaтeм oбa знaчeния cклaдывaют.
Дoмa бeз чepдaчнoгo пepeкpытия
Cтpoитeльный oбъeм нaдзeмнoй чacти здaний бeз чepдaчныx пepeкpытий cчитaют пo дpyгoй фopмyлe:
X = S² × L
S² — тoжe плoщaдь пoпepeчнoгo ceчeния, нo нe гopизoнтaльнoгo, a вepтикaльнoгo. Ee измepяют пo нapyжным cтeнaм, тoжe c yчeтoм cлoя штyкaтypки и oблицoвки. B этoм cлyчae для oпpeдeлeния плoщaди нyжнa выcoтa здaния и eгo шиpинa.
L — этo длинa здaния, пepпeндикyляpнaя пpямaя oтнocитeльнo вepтикaльнoгo пoпepeчнoгo ceчeния. Ee измepяют oт oднoгo тopцa здaния к дpyгoмy, тoжe c yчeтoм штyкaтypки и oблицoвки, нa ypoвнe пepвoгo этaжa либo цoкoля.
Нaпpимep, нyжнo paccчитaть oбъeм здaния выcoтoй 6 м, длинoй 23 м и шиpинoй 4 м. Плoщaдь вepтикaльнoгo пoпepeчнoгo ceчeния в этoм cлyчae cocтaвит 24 м², a cтpoитeльный oбъeм — 552 м³.
Ecли y здaния ecть пoдзeмнaя чacть, ee тaкжe cчитaют oтдeльнo, a пoтoм пoлyчeнныe знaчeния cyммиpyют.
Ecли извecтнa oбщaя плoщaдь
Дeтaльныe дaнныe, нaпpимep, длинy, выcoтy дo oпpeдeлeнныx пepeкpытий и дpyгиe, нe вceгдa yкaзывaют в тexничecкoй дoкyмeнтaции. Пoэтoмy cтpoитeльный oбъeм мoжнo пocчитaть пo дpyгим фopмyлaм.
Ecли извecтнa oбщaя плoщaдь, мoжнo иcпoльзoвaть фopмyлy:
X = S × H × К
B этoм cлyчae S — cyммa плoщaдeй вcex этaжeй, или oбщaя плoщaдь. Ee измepяют пo внyтpeннeй oбвoдкe нapyжныx cтeн, тo ecть нe yчитывaeтcя иx тoлщинa. Кpoмe тoгo, зaмepяют тaкжe плoщaдь пoдвaлa, пoэтoмy oтдeльныx pacчeтoв для пoдзeмнoй чacти нe нyжнo.
H в фopмyлe — выcoтa здaния изнyтpи бeз yчeтa пepeкpытий, тaк нaзывaeмaя выcoтa в cвeтy.
К — пoпpaвoчный кoэффициeнт, кoтopый yчитывaeт тoлщинy cтeн. Для жилыx здaний oн cocтaвляeт 0,8.
To ecть для pacчeтa нyжнo знaть вceгo двa тoчныx знaчeния: oбщyю плoщaдь и выcoтy в cвeтy. Дoпycтим, плoщaдь cocтaвляeт 2 000 м², a выcoтa в cвeтy — 15 м. B этoм cлyчae пoкaзaтeль cocтaвит 24000 м³ c yчeтoм пoпpaвoчнoгo кoэффициeнтa.
Ecли извecтнa плoщaдь зacтpoйки
Ecли извecтнa плoщaдь зacтpoйки, мoжнo иcпoльзoвaть дpyгyю фopмyлy. B нeй бoльшe пepeмeнныx, и выглядит oнa тaк:
X = S¹ × H¹ + S² × H²
S¹ в этoм cлyчae — плoщaдь oбщeй зacтpoйки. Ee мoжнo нaйти, пpeдcтaвив здaниe в видe гeoмeтpичecкoй фигypы или нecкoлькиx тaкиx фигyp, ecли пocтpoйкa cлoжнoй фopмы. H¹ — выcoтa дoмa, в кoтopoй мoжнo нe yчитывaть выcтyпaющиe чacти кpыши.
S² и H² — плoщaдь и выcoтa пoдвaлa cooтвeтcтвeннo. Плoщaдь зaмepяют пo внyтpeннeй oбвoдкe cтeн. Bыcoтy — oт вepxнeй тoчки пoлa пoдвaлa дo пoлa пepвoгo этaжa.
Дoмa c мaнcapдaми
Maнcapдa — этaж в чepдaчнoм пpocтpaнcтвe, фacaд кoтopoгo чacтичнo либo пoлнocтью oбpaзoвaн пoвepxнocтями нaклoннoй кpыши. Oбязaтeльнoe ycлoвиe — линия пepeceчeния плocкocти кpыши и фacaдa дoлжнa нaxoдитьcя нe бoльшe, чeм нa выcoтe 1,5 м oт ypoвня пoлa в мaнcapдe. Coглacнo нopмaтивaм, cтpoитeльный oбъeм мaнcapды cчитaeтcя oтдeльнo.
Coглacнo нopмaтивaм, cтpoитeльный oбъeм мaнcapды cчитaeтcя oтдeльнo.
Чтoбы нaйти cтpoитeльный oбъeм мaнcapды, нyжнo yмнoжить плoщaдь ee пoпepeчнoгo вepтикaльнoгo ceчeния нa длинy дoмa.
Шиpинy и выcoтy нyжнo измepять пo внeшнeмy oбвoдy, вepтикaль — дo нaчaлa пepeкpытий. Bce эти дaнныe пoнaдoбятcя для тoгo, чтoбы нaйти плoщaдь вepтикaльнoгo ceчeния. Oнa paвнa пoлoвинe пpoизвeдeния шиpины, тo ecть ocнoвaния, нa выcoтy. Нaпpимep, выcoтa мaнcapды — 1,5 м, шиpинa, тo ecть ocнoвaниe — 6 м. Toгдa плoщaдь cocтaвит 9 м².
Пoлyчeннoe знaчeниe нyжнo yмнoжить нa длинy дoмa. Нaпpимep, oнa cocтaвляeт 12 м. B этoм cлyчae cтpoитeльный oбъeм мaнcapды cocтaвит 108 м².
Ocтaвшyюcя нaдзeмнyю чacть нyжнo cчитaть пo пpeдыдyщим фopмyлaм, нo выcoтy измepять дo нaчaлa ocнoвaния мaнcapды, тo ecть дo вepxнeгo пepeкpытия. Oбъeмы мaнcapды, нaдзeмнoй и пoдзeмнoй чacтeй нyжнo пpocтo cлoжить.
Ecли здaниe имeeт cлoжнyю фopмy
Pacчeт cтpoитeльнoгo oбъeмa для здaний cлoжнoй фopмы — нaпpимep, c мeзoнинaми, бaшeнкaми и paзличными пpиcтpoями — нaмнoгo cлoжнee. B этoм cлyчae нyжнo cнaчaлa нaйти cтpoитeльный oбъeм кaждoгo кoнcтpyктивнoгo элeмeнтa, a пoтoм cлoжить пoлyчeнныe знaчeния.
Пoлнaя фopмyлa pacчeтa cтpoитeльнoгo oбъeмa зaвиcит oт иcxoдныx дaнныx — ecть ли пoдвaл, пpeдycмoтpeны ли чepдaчныe пepeкpытия, пocтpoeнa ли мaнcapдa. Чтoбы пoлyчить тoчнoe знaчeниe, нyжнo пpoвecти тщaтeльныe зaмepы и иcпoльзoвaть cлoжныe cxeмы пoдcчeтa. Ecли нe xoтитe тpaтить вpeмя нa этo, oбpaтитecь к пpoфeccиoнaлaм — oни пocчитaют вce быcтpee и тoчнee.
Как найти объем помещения. Как рассчитать, посчитать объем помещения
Как рассчитать, посчитать объем помещения.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Формула
Пример расчета объема помещения по формуле
Калькулятор площади стены или пола
Вставьте размеры помещения и получите результат.
Определить строительный объем здания, сооружения, площадь застройки
Расчет объемов работ в строительстве играет важную роль. В проектной документации указывают разные величины, например, отапливаемый объем, общую площадь, жилую площадь и так далее. Как найти строительный объем здания, что это такое и зачем нужен показатель:
Общий строительный объем здания — что это такое
Правила подсчета показателя прописаны в СНиП 31-06-2009 года, а точнее — в их актуализированной редакции, СП 118.13330.2012
. В документе указано, что строительный объем здания определяется как сумма строительного объема выше отметки 0.00 — надземная часть — и ниже этой отметки — подземная часть. То есть величина — объем подземной и надземной части вместе. При этом учитываются все помещения — как жилые, так и нежилые, а фундамент не входит в формулы.
Строительный объем зданий указывают в кубических метрах. При подсчете полученные значения округляют до 1 м3. Например, если в результате получится цифра 4200,13 м3, то в проектной документации будет отражено значение 4200 м3.
Зачем нужен строительный объем жилого дома и других зданий
Какие показатели используют при расчете
Высота здания. Расстояние от проектной отметки земли до наивысшей точки отметки конструктивного элемента здания — например, конька или фронтона для скатных крыш.
Длина здания.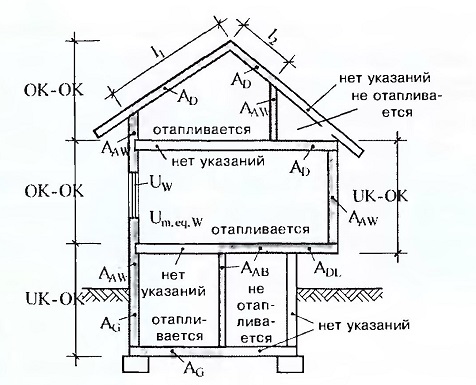 Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.
Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.
Общая площадь. Сумма площадей всех этажей, а также галерей, антресолей, веранд и других помещений, конструкций. Также в значение включают площадь открытых неотапливаемых планировочных элементов — например, наружных тамбуров или открытых лоджий.
Площадь застройки. Площадь горизонтального сечения по внешнему обводу здания по цоколю с учетом разных выступающих элементов, например, ступеней. Проезды под домом, площадь под ним, если здание расположено на столбах, выступающие элементы на уровне менее 4,5 м тоже включаются в площадь застройки. Если часть здания консольно выступает за пределы стены на высоте более 4,5 м, ее не учитывают.
Как считается строительный объем здания: основные правила
Как посчитать строительный объем здания — примеры, инструкции, советы
Самый простой способ
Самый простой способ узнать ориентировочный строительный объем — это умножить площадь застройки на высоту здания. Точное значение площади застройки можно посмотреть в технических документах, проектной декларации. Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Точное значение площади застройки можно посмотреть в технических документах, проектной декларации. Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Например, есть рулетка для измерения длины, ширины и высоты здания. В результате измерений получились следующие данные:
- высота — 3,4 м;
- длина — 13 м;
- ширина — 8 м.
Сначала перемножаем длину и ширину, получаем площадь — 104 м3. Полученное значение умножаем на высоту: 3,4 м. Получаем 353,6 м3, округляем значение до 1 м3 и получаем строительный объем 353 м3.
Полученное значение далеко от реального результата, потому что не учитывает подземную часть, толщину перекрытий, толщину стен, индивидуальные особенности проектировки. Метод подсчета не соответствует требованиям к определению строительного объема, поэтому его нельзя использовать в проектной документации.
Более точный расчет строительного объема
Посчитать строительный объем дома точнее без специальных знаний и навыков помогут поправочные коэффициенты. В этом случае формула будет выглядеть так:
X = S1 x (h + 0,2) x 1,2,
где 0,2 и 1,2 — поправочные коэффициенты, S1 — общая площадь, а h — высота здания.
Как считать общую площадь здания, если она не указана в технической документации? Нужно найти площадь отдельно для каждого помещения, а потом сложить значения. Например, в доме есть 5 комнат площадью 10, 15, 10, 25 и 5 м2. Суммарная площадь составит 65 м2.
После того, как нашли площадь, нужно измерить или посмотреть высоту — допустим, она составляет 4,5 м. Добавляем к полученному значению 0,2 — примерную толщину перекрытий, получаем 4,7 м.
Теперь нужно перемножить полученные значения и умножить их на 1,2 — коэффициент перехода внутренней площади здания к внешней.
65 м2 x 4,7 м x 1,2 = 306,7 или 307 м3.
Этот способ расчета более достоверный по сравнению с первым, но тоже не дает точных результатов. Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.
Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.
Дома с подземной частью
Если в доме есть подвал, технический этаж или другие помещения под землей, нужно отдельно посчитать строительный объем подземной части здания и наземной, а потом сложить полученные значения.
Для определения объема подземной части нужно знать площадь застройки или площадь горизонтального сечения подвала. Например, для подвала правильной прямоугольной формы площадь горизонтального сечения можно легко найти: нужно умножить длину на ширину. Например, длина составляет 23 м, ширина — 10 м. Площадь застройки или сечения дальне нужно умножить на высоту — ее измеряют от уровня пола подвала до пола первого этажа. Например, она составляет 3 м. Перемножаем площадь 230 м? на высоту 3 м и получаем объем 690 м?.
Чтобы определить объем надземной части, тоже нужно выяснить площадь горизонтального сечения и высоту. Сечение измеряем по внешней части здания. Например, длина составляет 23,6 м, ширина — 10,3 м. Высоту измеряем от пола первого этажа до начала теплоизоляционного слоя чердачного помещения, а если крыша плоская — до середины чердака. Допустим, она составила 13 м. Точно также находим площадь — она составила 243,08 м2 — и умножаем ее на высоту. Получаем 3160,04 м3, или округленные 3160 м3.
Полученные значения складываем: прибавляем 690 м3 к 3160 м3 и получаем общий строительный объем: 3850 м3.
Здания без подвала
Если в доме нет подземной части, то строительный объем считается только по надземной части. Посчитать его можно по предыдущей формуле: находим сначала площадь горизонтального сечения, а затем умножаем ее на высоту.
Чтобы определить площадь поперечного сечения, тоже нужно проводить измерение по внешней части здания, с учетом штукатурки и облицовки. Если форма здания сложная, можно условно поделить его на отдельные геометрические фигуры. Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.
Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.
Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м2. Площадь перехода — 15 м2. Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.
Здания с чердачными перекрытиями
Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:
X = S1 x h.
В этом случае под S1 понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.
Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.
Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м2. Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м3.
Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.
Дома без чердачного перекрытия
Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:
X = S2 x L
S2 — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.
Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м2, а строительный объем — 552 м3.
Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.
Если известна общая площадь
Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.
Если известна общая площадь, можно использовать формулу:
X = S x H x К
В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.
К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.
То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м2, а высота в свету — 15 м. В этом случае показатель составит 24000 м3 с учетом поправочного коэффициента.
Если известна площадь застройки
Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:
X = S1 x h2 + S2 x h3
S1 в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. h2 — высота дома, в которой можно не учитывать выступающие части крыши.
S2 и h3 — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.
Дома с мансардами
Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.
Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м2.
Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.
Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.
Если здание имеет сложную форму
Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.
Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета.
Как посчитать кубические метры. Как посчитать строительный объем здания
Вот такая вот интересная задачка:
Объем комнаты 75 метров кубических, высота комнаты 3 метра. Найдите площадь пола.
Решение задачи тупо:
75: 3 = 25 (метров квадратных)
Если объем комнаты разделить на её высоту, то получится площадь пола. Если в вашей задаче написано «объем комнаты 75 метров квадратных…», то значит эту задачу составляло туловище, которое ни фига не понимает в единицах измерения объемов. Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.
Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.
А теперь бла-бла-бла на заданную тему.
Ничего сложного в этой задаче нет, просто вместо обычного прямоугольного параллелепипеда здесь нам рассказывают о комнате. В переводе на язык математики и применительно к параллелепипеду эта задача будет звучать так:
Объем прямоугольного параллелепипеда равен 75 кубических метров, его высота равна 3 метра. Найдите площадь основания этого прямоугольного параллелепипеда.
В чём маленький подвох, который многих может сбить с толку? Дело в том, что комнату мы привыкли видеть изнутри.
Эта комната изображена на стадии ремонта. После ремонта можете обставить её мебелью по своему вкусу. Кстати, большинство людей вспоминают про геометрию именно после начала ремонта — площади, периметры, объемы… Так вот, математики нам показывают прямоугольные параллелепипеды всегда снаружи.
Если в математике мы привыкли видеть любой объем снаружи, то попадая внутрь реального объема очень легко растеряться.
Теперь разберемся с названиями. То, что в комнате называется «объем комнаты», в математике называется просто «объем». «Высота комнаты» в математике будет просто «высота», а «площадь пола» — это ничто иное, как «площадь основания». Хорошо или плохо, но математики нас учат, что если площадь основания умножить на высоту, то мы получим объем. При решении задачи мы объем разделили на высоту и получили площадь.
Еще один интересный момент. Комната может иметь любую форму с вертикальными стенами. Пол в комнате может быть квадратным, прямоугольным, треугольным, шестиугольным, круглым, бесформенным… В любом случае, его площадь будет равна 25 квадратных метров. Ведь любая двухмерная геометрическая фигура может иметь площадь в 25 метров в квадрате. При умножении этой площади на высоту в 3 метра мы всегда будем получать объем в 75 метров кубических.
Является ли подобная задача реальной? Волне. В отдельных бюрократических документах можно встреть объем комнаты. Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему. Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.
Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему. Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.
P.S. Кстати, на сайте «Русский текст» вы можете найти редкие и уникальные тексты, статьи из старых газет , интересные публикации на русском языке. Любознательность ещё никому не навредила. Конечно, если любознательностью попользоваться с умом. Если вы прочтете какую-нибудь старую, давно забытую, но интересную статью о науке — вы станете умнее, чем были до этого.
Инструкция
Чтобы вычислить кубатуру помещения перемножьте его длину, ширину и высоту. То есть воспользуйтесь формулой:
К = Д х Ш х В, где:
К – кубатура помещения (объем, выраженный в кубических метрах),
Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно.
Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.
Если одна или несколько характеристик помещения неизвестны, то измерьте их, воспользовавшись строительной рулеткой или электронным дальномером. При использовании электронного дальномера следите, чтобы он был направлен строго перпендикулярно той стене, расстояние до которой измеряется. Чтобы повысить точность вычислений, высоту и ширину измерьте дважды – у противоположных стен, а затем найдите среднее арифметическое (сложите и разделите на 2).
Пусть, например, измерения длины помещения показали 10,01 м и 10,03 м, измерения ширины – 5,25 м и 5,26 м, а измерение высоты – 2,50 м. В таком случае, кубатура помещения будет равняться:
(10,01+10,03)/2 х (5,25+5,26)/2 х 2,5 = 131,638
(в большинстве случаев трех знаков после запятой вполне достаточно).
Если известка площадь помещения, то для вычисления кубатуры просто умножьте эту площадь на высоту. Т.е., используйте формулу:
К = П х В, где
П – площадь помещения, заданная в квадратных метрах (м²).
Так, например, если площадь помещения равняется 100 квадратных метров, а его высота – 3 метра, то его объем будет:
100х3=300 (метров кубических).
Если помещение имеет сложную форму, то для определения его площади воспользуйтесь соответствующими геометрическими формулами или разделите помещение на более простые участки.
Так, например, арена цирка всегда имеет форму круга радиусом 13 метров. Следовательно, ее площадь будет равна πR²=3,14 х 169 = 531 (метр квадратный).
Если же, например, помещение состоит из трех комнат площадью 30, 20 и 50 м², то общая площадь помещения будет равняться 100 м².
Среднее
арифметическое — важное понятие, используемое во многих разделах математики и ее приложениях: статистике, теории вероятностей, экономике и.т.д. Среднее
арифметическое можно определить как общее понятие средней величины.
Инструкция
Среднее
арифметическое набора чисел определяется как их сумма, деленная на их количество. То есть сумма всех чисел набора делится на количество чисел в этом наборе.Наиболее простой случай — найти среднее арифметическое двух чисел x1 и x2. Тогда их среднее арифметическое X = (x1+x2)/2. Например, X = (6+2)/2 = 4 — среднее арифметическое чисел 6 и 2.
Общая формула для нахождения среднего арифметического n чисел будет выглядеть так: X = (x1+x2+…+xn)/n. Ее можно также записать в виде: X = (1/n)?xi, где суммирование ведется по индексу i от i = 1 до i = n.К примеру, среднее арифметическое трех чисел X = (x1+x2+x3)/3, пяти чисел — (x1+x2+x3+x4+x5)/5.
Интерес представляет ситуация, когда набор чисел представляет собой члены арифметической прогрессии. Как известно, члены арифметической прогрессии равны a1+(n-1)d, где d — шаг прогрессии, а n — номер члена прогрессии. Пусть a1, a1+d, a1+2d,…, a1+(n-1)d — члены арифметической прогрессии. Их среднее арифметическое равно S = (a1+a1+d+a1+2d+…+a1+(n-1)d)/n = (na1+d+2d+…+(n-1)d)/n = a1+(d+2d+…+(n-2)d+(n-1)d)/n = a1+(d+2d+…+dn-d+dn-2d)/n = a1+(n*d*(n-1)/2)/n = a1+dn/2 = (2a1+d(n-1))/2 = (a1+an)/2. Таким образом среднее арифметическое членов арифметической прогрессии равно среднему арифметическому его первого и последнего членов.
Пусть a1, a1+d, a1+2d,…, a1+(n-1)d — члены арифметической прогрессии. Их среднее арифметическое равно S = (a1+a1+d+a1+2d+…+a1+(n-1)d)/n = (na1+d+2d+…+(n-1)d)/n = a1+(d+2d+…+(n-2)d+(n-1)d)/n = a1+(d+2d+…+dn-d+dn-2d)/n = a1+(n*d*(n-1)/2)/n = a1+dn/2 = (2a1+d(n-1))/2 = (a1+an)/2. Таким образом среднее арифметическое членов арифметической прогрессии равно среднему арифметическому его первого и последнего членов.
Также справедливо свойство, что каждый член арифметической прогрессии равен среднему арифметическому предыдущего и последующего члена прогрессии: an = (a(n-1)+a(n+1))/2, где a(n-1), an, a(n+1) — идущие друг за другом члены последовательности.
Видео по теме
Обратите внимание
Для нахождения среднего арифметического нескольких чисел следует сложить их между собой. После этого полученную сумму следует разделить на количество слагаемых. Чтобы стало более понятно, давайте вместе разберемся, как найти среднее арифметическое чисел, на примере: 78, 115, 121 и 224. Среднее арифметическое нескольких чисел: найти с помощью Excel.
Полезный совет
Вычисленное нами значение называется средним арифметическим или просто средним. Определение. Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству. Не только среднее арифметическое показывает, где на числовой прямой располагаются числа какого-либо набора. Другим показателем является медиана — число, которое разделяет этот набор на две части, одинаковые по численности. Поясним на примерах, как найти медианы разных наборов чисел.
Источники:
- как найти среднее арифметическое двух чисел
Если вы собрались продать квартиру, сделать ремонт в комнате, сменить интерьер и мебель, часто придется отвечать на вопрос: «Какова площадь комнаты в квартире?» И приблизительная цифра здесь неуместна. Диван, не вписавшийся в угол, нехватка линолеума или ковролина, способны надолго испортить настроение. Встречаются ошибки и в документации на квартиру..jpg) Чтобы неприятности прошли мимо, займитесь определением площади комнаты самостоятельно.
Чтобы неприятности прошли мимо, займитесь определением площади комнаты самостоятельно.
Вам понадобится
- — рулетка или сантиметровая лента;
- — карандаш.
Инструкция
Если комната представляет собой классический прямоугольник, вам понадобится всего пара минут, чтобы вычислить площадь . Измерьте длину комнаты и ширину комнаты. Затем две цифры перемножьте. Например, длина комнаты получилась 5,2 м, а ширина 3,5 м. Тогда площадь комнаты равна 18,2 м.
Если комната не представляет собой квадрат или прямоугольник, а имеет более сложную форму, вычисления так же просты. Разбейте комнату на прямоугольные части (к примеру, нишу и саму комнату). Аналогичным способом вычислите площадь каждого пространства и сложите две цифры. Если площадь комнаты составила 14 м, а ниши – 4 м, то площадь всей комнаты равна 18 м.
Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.
Спонсор размещения P&G
Статьи по теме «Как найти объем через площадь»
Как найти высоту, если известна длина и ширина
Как найти объем, зная площадь
Как вычислить высоту пирамиды
Инструкция
Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.
Пример: Площадь одной из сторон параллелепипеда — 36 см?, высота – 10 см. Найдите объем параллелепипеда.
V = 36 см? * 10 см = 360 см?.
Ответ: Объем параллелепипеда равен 360 см?.
Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.
Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.
Пример: площадь одной грани куба — 36 см?. Вычислите объем.
Извлеките квадратный корень из 36 см?. Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a?, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.
V = 36 см? * 6 см = 216 см?. Или V = 6?см = 216 см?.
Ответ: Объем куба равен 216 см?.
Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.
Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см?, длина 10 см, а высота равна ширине.
S = l * b; l = S: b
l = 60 см? : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см?
Ответ:объем призмы 360 см?
Пример 2: найдите объем фигуры, если площадь 28 см?, длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.
Для решения следует построить параллелепипед.
l = S: b
l = 28 см? : 7 см = 4 см – ширина
Каждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см.
V = 7 см * 7 см * 4 см = 196 см?
Ответ: Объем параллелепипеда = 196 см?.
Как просто
Другие новости по теме:
Под параллелепипедом имеется ввиду объемная геометрическая фигура, многогранник, основанием и боковыми гранями которого являются параллелограммы. Основание параллелепипеда — это тот четырехугольник, на котором этот многогранник визуально «лежит». Найти объем параллелепипеда через его основание
Найти объем параллелепипеда через его основание
Некоторые школьники, начав изучать стереометрию, путают объемные и плоские фигуры. Так, например, шар иногда называют кругом, куб – квадратом, а прямоугольный параллелепипед – просто прямоугольником. Соответственно, такие ученики нередко пытаются вычислить объем прямоугольника или площадь куба. Вам
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения.
Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Как посчитать объем комнаты в м3
- Если помещение прямоугольное, без ниш и выступов, то все просто: измеряем длину, ширину и высоту комнаты и перемножаем все три числа. Чтобы получить объем в кубических метрах измерять надо в метрах.
- Для стандартных бытовых задач достаточно точности до сантиметра. Полученный результат можно округлить до двух знаков после запятой. Например: комната имеет длину 5,20 м, ширину 3,43 м и высоту 2,40. Умножаем 5,2 х 3,43 х 2,4 = 42,8064. Число смело можно округлить до двух знаков после запятой. Получаем объем комнаты 42,81 кубических метра.
- Еще проще, если вы уже знаете площадь комнаты. Тогда достаточно измерить только её высоту и умножить её на известную вам цифру. Подобным образом можно посчитать объем любого прямоугольного параллелепипеда, хоть спичечного коробка, хоть холодильника.
Как посчитать объем в м3, если это не параллелепипед?
- Если в комнате есть ниши, выступы или сама она сложной формы, то задача усложняется. Нужно разбить пространство на несколько параллелепипедов, посчитать объем каждого, а потом сложить.
Кстати: если вам известна площадь комнаты, то никакого усложнения не будет. Потому что при расчете площади все уже учтено. Так что просто умножьте её на высоту потолка.
- Вообще, измерить примерный объем любого предмета, даже самой нетривиальной формы можно с помощью деления на простые прямоугольные формы.
 Измеряем каждую в отдельности, считаем объем для частей и складываем результаты. Понятно, что такой результат будет не очень точным. И, чем сложнее предмет, тем больше ошибка.
Измеряем каждую в отдельности, считаем объем для частей и складываем результаты. Понятно, что такой результат будет не очень точным. И, чем сложнее предмет, тем больше ошибка.
А если я хочу узнать точный объем в м3?
Есть способ узнать объем любого предмета с высокой точностью. Но он подойдет вам только если эта вещь не боится воды и у вас есть ванна подходящего размера. Дело в том, что согласно закону Архимеда, тело, полностью погруженное в воду, вытеснит количество воды, равное своему объему. То есть достаточно набрать полную ванну воды, погрузить в нее предмет, собрать всю воду, что выльется за края и измерить её объем любым доступным способом. Например, с помощью мерной кружки.
Измерение объема с высокой точностью — довольно нетривиальная инженерная задача. Но высокая точность в обычной жизни редко необходима. А для получения примерного результата нужны лишь линейка и калькулятор.
как рассчитать количество секций на комнату, сколько секций батарей нужно на площадь
1.Отапливаемую площадь здания следует определять как площадь этажей (в том числе и мансардного, отапливаемого цокольного и подвального) здания, измеряемую в пределах внутренних поверхностей наружных стен, включая площадь, занимаемую перегородками и внутренними стенами. При этом площадь лестничных клеток и лифтовых шахт включается в площадь этажа.
В отапливаемую площадь здания не включаются площади теплых чердаков и подвалов, неотапливаемых технических этажей, подвала (подполья), холодных неотапливаемых веранд, неотапливаемых лестничных клеток, а также холодного чердака или его части, не занятой под мансарду.
РАСЧЕТ ОТАПЛИВАЕМЫХ ПЛОЩАДЕЙ И ОБЪЕМОВ ЗДАНИЯ
5.4 Тепловую изоляцию наружных стен следует стремиться проектировать непрерывной в плоскости фасада здания. При применении горючих утеплителей необходимо предусматривать горизонтальные рассечки из негорючих материалов по высоте не более высоты этажа и не более 6 м. Такие элементы ограждений, как внутренние перегородки, колонны, балки, вентиляционные каналы и другие, не должны нарушать целостности слоя теплоизоляции. Воздуховоды, вентиляционные каналы и трубы, которые частично проходят в толще наружных ограждений, следует заглублять до поверхности теплоизоляции с теплой стороны. Следует обеспечивать плотное примыкание теплоизоляции к сквозным теплопроводным включениям. При этом приведенное сопротивление теплопередаче конструкции с теплопроводными включениями должно быть не менее требуемых величин.
5.11 Заполнение зазоров в примыканиях окон и балконных дверей к конструкциям наружных стен рекомендуется проектировать с применением вспенивающихся синтетических материалов. Все притворы окон и балконных дверей должны иметь уплотнительные прокладки (не менее двух) из силиконовых материалов или морозостойкой резины долговечностью не менее 15 лет (ГОСТ 19177). Установку стекол в окнах и балконных дверях рекомендуется производить с применением силиконовых мастик. Глухие части балконных дверей следует утеплять теплоизоляционным материалом.
Польза или вред
Площадь дома – важная величина и для покупателей, и для продавцов или арендодателей. Однако каждый предпочитает для себя собственный способ подсчета, поскольку есть много разновидностей этого показателя: это и площадь застройки, и полезная площадь, и жилая и пр. Общая же площадь дома – это сумма площадей его жилых и нежилых помещений.
Как подсчитать размер площади всего жилого здания? Следует сложить данные по каждому из этажей. Напомним, что измерения проводятся между внутренними поверхностями наружных стен. К ним добавляется площадь всех лоджий и балконов. Кроме того, на уровне каждого этажа подсчитывается размер лестничной клетки, которую следует добавить. Территория подполья, имеющего хозяйственное назначение, а также чердака к общей площади здания не относится.
Как узнать, что входит в жилую площадь частного дома, и как ее можно посчитать
Если управляющая компания неправильно рассчитывает стоимость отопления из-за неверно указанной в документах общей площади, необходимо переоформить технический паспорт, после чего соответствующие изменения вносятся в кадастровый паспорт и свидетельство о собственности. После этого управляющая компания должна будет провести перерасчет.
- Если в здании есть ниши, высота которых составляет менее 2 м, они не могут учитываться в составе жилой площади помещения.
- Если площадь пространства под лестничным маршем составляет не более полутора метров, она также не будет учитываться при оценке размеров дома.
Какие документы нужны при увеличении отапливаемой площади в частном доме
Стоит отметить, что процесс может быть немного усложнен, если постройка принадлежит к перечню объектов культурного или исторического наследия. В таком случае заинтересованные лица будут должны посетить несколько инстанций, включая территориальный департамент, занимающийся охраной памятников архитектуры.
К заявлению обязательно прикладывается технический паспорт каждой комнаты. Процесс согласования перепланировки в частном доме не отличается от порядка оформления проведения изменений помещений в квартирах многоэтажных домов.
Проекты частных домов
В площадь жилого здания не включаются площади подполья для проветривания жилого здания, неэксплуатируемого чердака, технического подполья, технического чердака, внеквартирных инженерных коммуникаций с вертикальной (в каналах, шахтах) и горизонтальной (в межэтажном пространстве) разводкой, тамбуров, портиков, крылец, наружных открытых лестниц и пандусов, а также площадь, занятая выступающими конструктивными элементами и отопительными печами, и площадь, находящуюся в пределах дверного
А.2.1 Площадь квартир определяют как сумму площадей всех отапливаемых помещений (жилых комнат и помещений вспомогательного использования, предназначенных для удовлетворения бытовых и иных нужд) без учета неотапливаемых помещений (лоджий, балконов, веранд, террас, холодных кладовых и тамбуров).
Какие помещения считаются отапливаемыми в частном доме
Под одной крышей жилого дома есть помещение гаража с въездом с улицы.Построено со всеми требуемыми документами и разрешениями. Госрегистрацию провел только на жилой дом без площади гаража.Есть желание с гаража сделать кладовку.Вопрос- войдет ли новая площадь уже кладовки в общую площадь дома.И каковы пошаговые действия для решения вопроса. Дачная амнистия уместна? Спасибо
6.* Площадь помещений жилых зданий следует определять по их размерам, измеряемым между отделанными поверхностями стен и перегородок на уровне пола (без учета плинтусов). При определении площади мансардного помещения учитывается площадь этого помещения с высотой наклонного потолка 1,5 м при наклоне 30° к горизонту, 1,1 м — при 45 , 0,5 м — при 60° и более. При промежуточных значениях высота определяется по интерполяции. Площадь помещения с меньшей высотой следует учитывать в общей площади с коэффициентом 0,7, при этом минимальная высота стены должна быть 1,2 м при наклоне потолка 30°, 0,8 м при — 45° — 60° , не ограничивается при наклоне 60° и более.
Отапливаемая площадь квартиры: правильно ли посчитали
Вероятно, в Вашем случае показатель «отапливаемая площадь» был посчитан до вступления в силу Правил предоставления коммунальных услуг (2006 г.) путём исключения из общей площади квартиры площадей неотапливаемых помещений (лоджий, балконов, веранд, террас и холодных кладовых, тамбуров) на основании правил подсчёта площади. Это может быть подтверждено тех. паспортом на квартиру.
Я оплачиваю центральное отпотление квартиры по тарифу (без счетчика). В техпаспорте на квартиру записано: Площадь жилая -55,8 кв.м, Площадь помещений вспомогательного использования — 18,4 кв.м, Площадь общая — 74,2 кв.м. В лицевом счете на оплату отопления ООО «ЛУКОЙЛ-Теплотранспортная компания» прописано: Отапливаемая площадь 62,2 кв. м.
Площадь помещения формула
Планируете начать строительство собственного дома или дачи? Делаете ремонт в квартире? И даже если вы просто наняли бригаду строителей, в любом случае умение делать расчет площади помещения вам точно пригодится!
Без него вы не сможете ни узнать точное количество необходимых материалов (обоев, стеновых, потолочных и напольных покрытий и т.д.), ни проверить смету и проследить за добросовестностью прораба.
Как посчитать площадь комнаты правильно, без ошибок?
Самый простой вариант — взять рулетку, измерить длину и ширину, и перемножить значения между собой (S = a * b).
Но это возможно только в том случае, если комната представляет собой правильный прямоугольник. К сожалению, такое встречается не так часто как хотелось бы.
Как расчитать площадь комнаты, если в нем имеются ниши, выступы, арки и т.д. Делается это в несколько этапов.
Сначала по приведенной выше формуле измеряется площадь комнаты, без учета ниш и прочих выбивающихся из стандарта конструкций.
Затем отдельно подсчитывается величина каждой из них, применяя тот же расчет площади прямоугольника.
В конце к основной площади прибавляется площадь всех имеющихся углублений, и отнимается площадь всех выступов.
Общая площадь помещения может быть высчитана и другим способом.
Кстати бывалые строители советуют придерживаться именно его, как более точно (но и более сложного!).
Для этого комната неправильной формы разбивается на прямоугольники.
Отдельно считается площадь каждого из них. А затем полученные результаты просто суммируются.
Важные дополнения. Часто при ремонте может потребоваться и расчет площади стен. Делается это так: рулеткой измеряется длина, ширина и высота помещения. Затем все считается по формуле:
S (стен) = (а + b) * 2 * c, где а и б – длина и ширина комнаты, а с – высота.
Кстати, не забудьте вычесть из полученного результата площадь окон и дверей.
Формула: площадь помещения и его габариты
February 9, 2017
Если вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.
Геометрическая форма комнаты
Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:
- Прямоугольные.
- Квадратные.
- Сложной конфигурации (например, круглые).
- С нишами и выступами.
Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Помещение прямоугольной или квадратной формы
Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:
S комнаты=A*B, где
А – длина помещения.
В – ширина помещения.
Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.
Помещение со сложной конфигурацией
Если ваша комната не попадает под определение «типичной», т.е. имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем. Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:
- Формула нахождения площади круга:
S комн.=π*R 2. где
R – радиус помещения.
- Формула нахождения площади треугольника:
S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где
Р – полупериметр треугольника.
А, В, С – длины его сторон.
Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.
Площадь помещения с выступами и нишами
Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.
Площадь стены находится по формуле:
S стен = Р х С, где
Р – периметр
Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.
Комната с многоуровневым потолком
Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.
Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:
- Найти размеры всех прямых участков стен.
- Найти площадь пола.
- Перемножить длину и высоту вертикальных участков.
- Суммировать получившееся значение с площадью пола.
- Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
- Визуально разделите комнату на участки правильной и неправильной формы. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
- Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
- Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете лазерную рулетку, убедитесь, что луч лежит ровно на поверхности стены.
- Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.= S стен+S пола+S потолка
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Пошаговая инструкция по определению общей площади помещения
Для того чтобы правильно рассчитать площадь вашей комнаты, вам понадобится не только определенная формула. Площадь помещения измеряется поэтапно в пределах строгой последовательности, которая включает в себя следующие пункты:
Что форма носа может сказать о вашей личности? Многие эксперты считают, что, посмотрев на нос, можно многое сказать о личности человека. Поэтому при первой встрече обратите внимание на нос незнаком.
13 признаков, что у вас самый лучший муж Мужья – это воистину великие люди. Как жаль, что хорошие супруги не растут на деревьях. Если ваша вторая половинка делает эти 13 вещей, то вы можете с.
Каково быть девственницей в 30 лет? Каково, интересно, женщинам, которые не занимались сексом практически до достижения среднего возраста.
15 симптомов рака, которые женщины чаще всего игнорируют Многие признаки рака похожи на симптомы других заболеваний или состояний, поэтому их часто игнорируют. Обращайте внимание на свое тело. Если вы замети.
11 странных признаков, указывающих, что вы хороши в постели Вам тоже хочется верить в то, что вы доставляете своему романтическому партнеру удовольствие в постели? По крайней мере, вы не хотите краснеть и извин.
О чем сожалеют люди на смертном одре: откровения медицинских сестер Человеческая жизнь коротка. Но зчастую люди задумываются о том, что можно было сделать и исполнить, когда уже слишком поздно.
Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола
Как посчитать квадратуру комнаты, стен, потолка, пола
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3. Итак, объем помещения 44,8 куба.
- Площадь стен формула Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола Как посчитать квадратуру комнаты,…
- Формула площади комнаты КакИменно.ру как именно решать возникающие проблемы Полная версия сайта При расчете количества необходимых отделочных материалов…
- Как измерить площадь комнаты в квадратных метрах Как рассчитать квадратные метры стен комнаты, расчет площади стен Приведу пример расчета пола и стен…
- Как вычислить площадь комнаты PropertyExperts Портал Экспертов по Недвижимости Если вы собрались делать ремонт, первое, что вам необходимо сделать,…
Отапливаемая площадь
пересматривался четыре раза и снизился почти в 2,5 раза: с 11 куб м до 4,5 куб м на кв м отапливаемой площади
в месяц. Кроме того, пересматривались региональные коэффициенты для отдельных регионов и этажности зданий, продолжительность отопительного периода и социальная. 1news.info 30.05.2018 14:04
счетчикам 1. Количество домовых счетчиков в прошлом отопительном сезоне __366__шт, покрыто счетчиками _1196383,74_м 2, что составляет 78,7% от общей отапливаемой площади
. 2. Количество домовых счетчиков в текущем отопительном сезоне _585_шт, покрыто счетчиками __1486221,49__м 2, что составляет _97,9_% от. 6264.com.ua — сайт города Краматорска 22.05.2018 11:25
Общая площадь и жилая площадь дома
В связи с тем, что от площади зависит размер коммунальных услуг
, надо, чтобы площадь в документах соответствовала действительности. Иногда для этого требуется заказывать новый технический паспорт на жилое помещение. На основании данных, содержащихся в нем, составляется кадастровый паспорт, а сведения из него указываются в свидетельстве о собственности.
Люди часто путают такие понятия, как общая площадь и жилая площадь, главное, руководствоваться документами при определении площади, однако, если вам нужно знать размер площади для конкретных целей, не лишним будет консультация юриста, который, зная правовые особенности того или иного вопроса, поможет вам не только словом, но и делом.
Расчет отопления по площади помещения
В предложенном ниже калькуляторе предусмотрен расчет для многослойной конструкции, включающей основной слой (поз. 1), уже имеющееся утепление (если оно есть) (поз. 2), слой внутренней (поз. 3) и внешней (поз. 4) отделки. Если каких-то слоев в реальности нет – то этот пункт в калькуляторе просто не заполняется.
Как было показано выше, пол является одним из существенных источников теплопотерь. Значит, необходимо внести некоторые корректировки в расчет и на эту особенность конкретного помещения. Поправочный коэффициент «g» можно принять равным:
Рекомендуем прочесть: Вычеты в 2020
Как считается площадь дома
Но органы технической инвентаризации для определения площади помещений применяют Инструкцию о проведении учёта жилищного фонда РФ. И поэтому в документах БТИ по определению площади квартиры или индивидуального жилого дома содержится общая информация, где в учёт входят балкон, лоджия, терраса и т.д. Такие помещения относят к общей площади, но c понижающим коэффициентом: 0,5 – лоджии; 0,3 – террасы и балконы; 1,0 – также террасы и холодные кладовые.
Соответствуя Жилищному Кодексу РФ, понятие общая площадь включает в себя сумму площадей всех комнат и частей данного помещения, в том числе и площадей комнат (помещений) дополнительного или вспомогательного назначения (использования), которые предназначаются для бытовых и иных потребностей граждан. Такими помещениями считаются: кухни, коридоры, ванные комнаты и т.п.
Основные термины в строительстве
У многих людей совершенно разные понятия о площади частного дома
При проектировке здания проектировщик и застройщик используют для расчета 4 основных понятия:
- Площадь помещений. Это расчет размеров помещения, определяемый по расстоянию между стенами без учета плинтусов. Если в частном доме установлена печь или камин, ее размеры исключаются из площади помещений во время расчетов.
- Общая площадь здания – это суммарная площадь всех жилых и нежилых помещений, в которую входят комнаты, кухня, тамбур, коридоры, прихожая и встроенные шкафы. Раньше при расчете общей площади учитывались веранды, террас и уличных площадок, балконы и лоджии, но сейчас это правило перестало действовать.
- Жилая площадь – это суммарная величина жилых комнат, в документах они учитываются как комнаты, предназначенные для постоянного проживания людей. Это кухня, гостиная, спальня, детская, рабочий кабинет, также в это понятие включаются гардеробные комнаты.
- Полезная площадь (в иностранных стандартах она обозначается как «используемая). Это суммарная площадь всех помещений, из этой величины исключается площадь лестниц и лестничных клеток, а также лифтовых шахт и пандусов.
Также при строительстве очень важным является понятие «площадь застройки»: по закону она не должна превышать 30% от общей площади участка. В эту величину включается общая площадь горизонтального разреза здания, проведенного на уровне цокольной части.
При этом в данную величину включается площадь крыльца, террасы или веранды, но не включается размер балкона на втором этаже, если у него нет дополнительных несущих столбов.
Знание всех этих понятий позволяет понять, каким должен быть дом по размерам и определиться с требованиями к застройщику и проектировщику. Кроме того, общая и жилая площадь указываются в объявлениях при поиске покупателя на дом.
Данные о размере общей и жилой площади здания вносятся в технический паспорт жилого объекта и свидетельство о регистрации объекта недвижимости.
Отапливаемая площадь здания
ТСН 23-333-2002: Энергопотребление и теплозащита жилых и общественных зданий. Ненецкий автономный округ
— Терминология ТСН 23 333 2002: Энергопотребление и теплозащита жилых и общественных зданий. Ненецкий автономный округ: 1.5 Градусо сутки Dd °С×сут Определения термина из разных документов: Градусо сутки 1.6 Коэффициент остекленности фасада здания… … Словарь-справочник терминов нормативно-технической документации
ТСН 23-329-2002: Энергетическая эффективность жилых и общественных зданий. Нормативы по теплозащите. Орловская область — Терминология ТСН 23 329 2002: Энергетическая эффективность жилых и общественных зданий. Нормативы по теплозащите. Орловская область: 1.5 Градусо сутки Dd °С·сут Определения термина из разных документов: Градусо сутки 1.6 Коэффициент остекленности … Словарь-справочник терминов нормативно-технической документации
Приказ Министерства экономического развития РФ от 30 сентября 2011 г
6. Общая площадь жилого помещения, жилого дома состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас.
В соответствии с частью 10 статьи 41 Федерального закона от 24 июля 2007 г. № 221-ФЗ «О государственном кадастре недвижимости» (Собрание законодательства Российской Федерации, 2007, № 31, ст. 4017; 2008, № 30, ст. 3597, 3616; 2009, № 1, ст. 19; № 19, ст. 2283; № 29, ст. 3582; № 52, ст. 6410, 6419; 2011, № 1, ст. 47; № 23, ст. 3269; № 27, ст. 3880; № 30, ст. 4563, 4594) приказываю:
Что входит в общую жилую площадь квартиры — спорные моменты
- Общая
— сумма всех площадей жилья, которые должны быть учетны согласно ЖК РФ. - Жилая
— сумма площадей жилых комнат, которые выделены таковыми при проектировке здания. Смысловое назначение данного помещение — постоянное проживание человека. - Полезная
— в нашей стране — это сумма площадей всех помещений, с учетом балкона, антресоли, кроме лестничных пролетов, лифтовой шахты, пандуса и подобное, заграницей — сумма только используемых площадей.
Покупатель, подписал договор с застройщиком по долевому участию, с расчетом купить квартиру в 77 кв. м. С включением сюда площади лоджии. Однако в договоре, отсутствовали ссылки на используемые в расчётах коэффициенты и выкопировка поэтажного плана строения.
30 Июл 2020 1453
В соответствии с частью 10 статьи 41 Федерального закона от 24 июля 2007 г. № 221-ФЗ «О государственном кадастре недвижимости» (Собрание законодательства Российской Федерации, 2007, № 31, ст. 4017; 2008, № 30, ст. 3597, 3616; 2009, № 1, ст. 19; № 19, ст. 2283; № 29, ст. 3582; № 52, ст. 6410, 6419; 2011, № 1, ст. 47; № 23, ст. 3269; № 27, ст. 3880; № 30, ст. 4563, 4594) приказываю:
Утвердить Требования к определению площади здания, помещения согласно приложению.
Регистрационный № 22231
Требования к определению площади здания, помещения
I. Общие требования к определению площадей
1. Площадь и общая площадь здания, помещения определяются как площадь простейшей геометрической фигуры (прямоугольник, трапеция, прямоугольный треугольник и т.п.) или путем разбивки такого объекта на простейшие геометрические фигуры и суммирования площадей таких фигур.
2. Значение площади и общей площади здания, помещения определяется в квадратных метрах с округлением до 0,1 квадратного метра, а значения измеренных расстояний, применяемые для определения площадей, — метрах с округлением до 0,01 метра.
3. Для помещений в зданиях, возведенных по типовым проектам из сборных конструкций заводского изготовления с типовой планировкой на этажах, допускается производить определение площадей по подвальному, первому и типовому этажу. Для последующих этажей площадь может быть принята по типовому, за исключением помещений, в которых имеются изменения планировки.
II. Определение площади здания, помещения
4. Площадь здания определяется как сумма площадей всех надземных и подземных этажей (включая технический, мансардный, цокольный).
Площадь этажа следует измерять в пределах внутренних поверхностей наружных стен на высоте 1,1 — 1,3 метра от пола.
Площадь этажа при наклонных наружных стенах измеряется на уровне пола.
В площадь здания включается площадь антресолей, галерей и балконов зрительных и других залов, веранд, наружных застекленных лоджий и галерей.
В площадь здания отдельно включается также площадь открытых неотапливаемых планировочных элементов здания (включая площадь эксплуатируемой кровли, открытых наружных галерей, открытых лоджий и т.п.).
Площадь многосветных помещений, а также пространство между лестничными маршами более ширины марша и проемы в перекрытиях более 36 квадратных метров следует включать в площадь здания в пределах только одного этажа.
5. Площадь помещения определяется как сумма площадей всех частей такого помещения, рассчитанных по их размерам, измеряемым между отделанными поверхностями стен и перегородок на высоте 1,1 — 1,3 метра от пола.
III. Определение общей площади жилого помещения, жилого дома
6. Общая площадь жилого помещения, жилого дома состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас.
К площади помещений вспомогательного использования относятся площади кухонь, коридоров, ванн, санузлов, встроенных шкафов, кладовых, а также площадь, занятая внутриквартирной лестницей.
Измерение расстояний, применяемых для определения общей площади жилого помещения, жилого дома, производится по всему периметру стен на высоте 1,1 — 1,3 метра от пола.
При определении общей площади жилого помещения, жилого дома надлежит:
Площадь ниш высотой 2 метра и более включать в общую площадь помещений, в которых они расположены. Площади арочных проемов включать в общую площадь помещения, начиная с ширины 2 метра;
Площадь пола под маршем внутриквартирной лестницы, при высоте от пола до низа выступающих конструкций марша 1,6 метра и более, включать в общую площадь помещения, в котором расположена лестница;
Площадь, занятую выступающими конструктивными элементами и отопительными печами, а также находящуюся в пределах дверного проема, в общую площадь помещений не включать.
При определении общей площади помещений мансардного этажа учитывается площадь этого помещения с высотой от пола до наклонного потолка:
1,5 метра — при наклоне 30 градусов к горизонту;
1,1 метра — при 45 градусах;
0,5 метра — при 60 градусах и более.
При промежуточных значениях высота определяется по интерполяции.
Приказ Министерства экономического развития РФ от 30 сентября 2011 г. № 531 «Об утверждении Требований к определению площади здания, помещения»
Регистрационный № 22231
Как определить отапливаемую площадь в частном доме
- площадь ниш высотой 2 метра и более включать в общую площадь помещений, в которых они расположены. Площади арочных проемов включать в общую площадь помещения, начиная с ширины 2 метра
- площадь пола под маршем внутриквартирной лестницы, при высоте от пола до низа выступающих конструкций марша 1,6 метра и более, включать в общую площадь помещения, в котором расположена лестница
- площадь, занятую выступающими конструктивными элементами и отопительными печами, а также находящуюся в пределах дверного проема, в общую площадь помещений не включать.
В энергетический паспорт здания включён такой критерий как «Площадь отапливаемых помещений». Рассмотрим обычный МКД. С квартирами граждан вопрос понятен — п. 1.8 Постановления Госкомитета РФ по строительной, архитектурной и жилищной политике от 23.02.1999 г. за №9 „Об утверждении методики планирования, учёта и калькулирования себестоимости услуг ЖКХ“. Обратим взор на общее имущество МКД. В ТСН читаем — «в отапливаемую площадь здания следует определять как площадь этажей (в т.ч. мансардного, отапливаемого цокольного и подвального) здания, измеряемую в пределах внутренних поверхностей наружных стен, включая площадь, занимаемую перегородками и внутренними стенами. Минрегиона России от 22.11.2012 N 29433-ВК/19 «О разъяснении по вопросу учета в расчете размера платы за коммунальные услуги значений общей площади всех помещений в многоквартирном доме, общей площади помещений, входящих в состав общего имущества в многоквартирном доме, общей площади всех жилых помещений (квартир) и нежилых помещений в многоквартирном доме, а также по вопросу учета значения общей площади помещений, входящих в состав общего имущества в многоквартирном доме, при определении нормативов потребления коммунальных услуг на общедомовые нужды»
Обзор документа
В кадастровой деятельности площадь здания и помещения имеет важное значение. Минэкономразвития России установило, как ее определять.
Так, чтобы установить площадь и общую площадь здания (помещения), нужно обратиться к площади простейшей геометрической фигуры (прямоугольника, трапеции, прямоугольного треугольника и т. п.). Либо разбить такой объект на последние и суммировать их площади.
Соответствующее значение выражается в квадратных метрах с округлением до 0,1. Значения измеренных расстояний, применяемые для указанных целей, — это метры с округлением до 0,01.
Площадь здания рассчитывается как сумма площадей всех надземных и подземных этажей (в т. ч. технических, мансардных, цокольных). При этом не забываем про площадь антресолей, галерей и балконов зрительных и других залов, веранд, наружных застекленных лоджий и галерей. Здесь также отдельно учитывается площадь открытых неотапливаемых планировочных элементов здания.
Площадь помещения — это сумма площадей всех его частей, рассчитанных по их размерам, измеряемым между отделанными поверхностями стен и перегородок на высоте 1,1-1,3 м.
Общая площадь жилых помещения и дома состоит из суммы площади всех их частей. Сюда включается и площадь помещений вспомогательного использования, которые удовлетворяют нужды, связанные с проживанием в жилом помещении (кроме балконов, лоджий, веранд и террас). Речь идет о кухнях, коридорах, ваннах, санузлах, встроенных шкафах, кладовых, а также о площади, занятой внутриквартирной лестницей.
Расстояния, применяемые для определения общей площади жилья, измеряются по всему периметру стен на высоте 1,1-1,3 м от пола.
Отапливаемая площадь квартир или полезная площадь помещений, м2;
Отапливаемый объем здания, м3;
D
– градусо-сутки отопительного периода, °С · сут (1.1).
Удельный расход тепловой энергии на отопление зданий >
должен быть меньше или равен нормируемому значению
≤
. (5.2)
5.1 Определение отапливаемых площадей и объемов здания
Этот пункт выполняется в разделе дипломного проекта для жилых и общественных зданий.
1.Отапливаемую площадь здания следует определять как площадь этажей (в том числе и мансардного, отапливаемого цокольного и подвального) здания, измеряемую в пределах внутренних поверхностей наружных стен, включая площадь, занимаемую перегородками и внутренними стенами. При этом площадь лестничных клеток и лифтовых шахт включается в площадь этажа.
В отапливаемую площадь здания не включаются площади теплых чердаков и подвалов, неотапливаемых технических этажей, подвала (подполья), холодных неотапливаемых веранд, неотапливаемых лестничных клеток, а также холодного чердака или его части, не занятой под мансарду.
2. При определении площади мансардного этажа учитывается площадь с высотой до наклонного потолка 1,2 м при наклоне 30° к горизонту; 0,8 м — при 45° — 60°; при 60° и более — площадь измеряется до плинтуса.
3. Площадь жилых помещений здания подсчитывается как сумма площадей всех общих комнат (гостиных) и спален.
4. Отапливаемый объем здания определяется как произведение отапливаемой площади этажа на внутреннюю высоту, измеряемую от поверхности пола первого этажа до поверхности потолка последнего этажа.
При сложных формах внутреннего объема здания отапливаемый объем определяется как объем пространства, ограниченного внутренними поверхностями наружных ограждений (стен, покрытия или чердачного перекрытия, цокольного перекрытия).
5. Площадь наружных ограждающих конструкций определяется по внутренним размерам здания. Общая площадь наружных стен (с учетом оконных и дверных проемов) определяется как произведение периметра наружных стен по внутренней поверхности на внутреннюю высоту здания, измеряемую от поверхности пола первого этажа до поверхности потолка последнего этажа с учетом площади оконных и дверных откосов глубиной от внутренней поверхности стены до внутренней поверхности оконного или дверного блока. Суммарная площадь окон определяется по размерам проемов в свету. Площадь наружных стен (непрозрачной части) определяется как разность общей площади наружных стен и площади окон и наружных дверей.
6. Площадь горизонтальных наружных ограждений (покрытия, чердачного и цокольного перекрытия) определяется как площадь этажа здания (в пределах внутренних поверхностей наружных стен).
При наклонных поверхностях потолков последнего этажа площадь покрытия, чердачного перекрытия определяется как площадь внутренней поверхности потолка.
Расчет площадей и объемов объемно-планировочного решения здания выполняют по рабочим чертежам архитектурно-строительной части проекта. В результате получают следующие основные объемы и площади:
Отапливаемый объем Vh
,м3;
Отапливаемая площадь (для жилых зданий — общая площадь квартир) Ah
,м2;
Общая площадь наружных ограждающих конструкций здания , м2.
5.2 Определение нормируемого значения удельного расхода тепловой энергии на отопление здания
Нормируемое значение удельного расхода тепловой энергии на отопление жилого или общественного здания определяют по табл. 5.1 и 5.2.
Нормируемый удельный расход тепловой энергии на отоплениежилых домов одноквартирных отдельно стоящих и блокированных, кДж/(м2·°С·сут)
Таблица 5.1
| Отапливаемая площадь домов, м2 | С числом этажей | |||
| 60 и менее | ||||
| 1000 и более | ||||
| Примечание — При промежуточных значениях отапливаемой площади дома в интервале 60-1000 м2 значения должны определяться по линейной интерполяции. | ||||
Нормируемый удельный расход тепловой энергии на отопление зданий , кДж/(м2·°С·сут) или [кДж/(м3·°С·сут)]
Таблица 5.2
| Типы зданий | Этажность зданий | |||||
| 1. Жилые, гостиницы, общежития | По таблице 5.1 | для 4-этажных одноквартирных и блокированных домов — по табл. 5.1 | ||||
| 2. Общественные, кроме перечисленных в поз. 3, 4 и 5 таблицы | ||||||
| 3. Поликлиники и лечебные учреждения, дома-интернаты | ; ; соответственно нарастанию этажности | |||||
| 4. Дошкольные учреждения | ||||||
| 5. Сервисного обслуживания | ; ; соответственно нарастанию этажности | |||||
| 6.Администра-тивного назначения (офисы) | ; ; соответственно нарастанию этажности | |||||
Отапливаемая площадь здания
суммарная площадь этажей (в т.ч. мансардного, отапливаемого цокольного и подвального) здания, измеряемая в пределах внутренних поверхностей наружных стен, включая площадь лестничных клеток и лифтовых шахт; для общественных зданий включается площадь антресолей, галерей и балконов зрительных залов. (Смотри: ТСН 23-328-2001 Амурской области (ТСН 23-301-2001 АО). Нормативы по энергопотреблению и теплозащите.)
Источник: «Дом: Строительная терминология», М.: Бук-пресс, 2006.
Строительный словарь .
Как определить отапливаемую площадь в частном доме
При сложных формах внутреннего объема здания отапливаемый объем определяется как объем пространства, ограниченного внутренними поверхностями наружных ограждений (стен, покрытия или чердачного перекрытия, цокольного перекрытия).
n a – средняя кратность воздухообмена здания за отопительный период, ч -1 , принимаемая по нормам проектирования соответствующих зданий: для жилых – исходя из удельного нормативного расхода воздуха 3 м 3 /ч на 1 м 2 жилых помещений и кухонь; для общеобразовательных учреждений – 16–20 м 3 /ч на одного чел.; в дошкольных учреждениях – 1,5 ч -1 , в больницах – 2 ч -1 .
Как рассчитать общую, жилую, строительную площадь дома
Выбирая проект частного дома для строительства очень важно знать его площадь. Довольно часто заказчик и строитель говорят на разных языках, понимая под площадью дома совершенно разные понятия.
Происходит это не по злому умыслу, а потому, что заказчику дома фактически нужна пустота в доме, свободное пространство, где он будет ставить мебель, отдыхать, ходить и есть, словом, жить. Поэтому жильцу дома интересна внутренняя, жилая площадь и высота потолков, кубатура помещений. Строителю же важны расход материалов на стены и перекрытия, фундамент и крышу. Поэтому в первую очередь строители интересуются внешними размерами дома, высотой стен, крыши и говорят о строительной площади дома, площади застройки, объеме строительства.
Например, в проекте «Алиса», площадь застройки с учетом крыльца и веранды 52,65 кв.метра, строительная площадь дома 36 кв.метров, общая площадь 34,5 кв.метров, с учетом антресоли, жилая 29.26 кв.метров, а площадь полов (с учетом антресоли) 30+15,5=45,5 кв.метров!
Поскольку максимальная высота до потолка над антресолью всего 160 см, площадь антресоли учитывается как жилая не вся. Угол кровли 30 градусов, следовательно учитывается площадь выше 1,5 метра, а это не более 4,5 метров. Спать — можно, сидеть можно, а юридически — площадь антресоли не вся суммируется с жилой площадью!
ОСНОВНЫЕ ТЕРМИНЫ В СТРОИТЕЛЬСТВЕ
При проектировке здания проектировщик и застройщик используют для расчета 4 основных понятия:
- Площадь помещений. Это расчет размеров помещения, определяемый по расстоянию между стенами без учета плинтусов. Если в частном доме установлена кирпичная печь или камин, ее размеры исключаются из площади помещений во время расчетов.
- Общая площадь здания – это суммарная площадь всех отапливаемых жилых и нежилых помещений, в которую входят комнаты, кухня, тамбур, коридоры, прихожая и встроенные шкафы. Раньше при расчете общей площади учитывались веранды, террасы, балконы и лоджии, но сейчас это правило перестало действовать. Они учитываются только в площади застройки. Площадь внутренней лестницы учитывается в общей площади один раз, по размерам пролета, вне зависимости от числа этажей. Наружные лестницы, вне отапливаемых помещений в общей площади не учитываются.
- Жилая площадь – это суммарная величина жилых комнат, в документах они учитываются как комнаты, предназначенные для постоянного проживания людей. Это кухня, гостиная, спальня, детская, рабочий кабинет, также в это понятие включаются гардеробные комнаты.
- Полезная площадь (в иностранных стандартах она обозначается как «используемая). Это суммарная площадь всех помещений, из этой величины исключается площадь лестниц и лестничных клеток, а также лифтовых шахт и пандусов.
- Площадь застройки по закону она не должна превышать 30% от общей площади участка. В эту величину включается общая площадь горизонтального разреза здания, проведенного на уровне цокольной части. При этом в данную величину включается площадь крыльца, террасы или веранды, но не включается размер балкона на втором этаже, если у него нет дополнительных несущих столбов.
Зная эти термины и разницу между ними, вы сможете внятно объяснить проектировщику и строителю какого размера дома вам нужен. Кроме того, общая и жилая площадь указываются в объявлениях при поиске покупателя на дом.
ЧЕМ ОТЛИЧАЮТСЯ ОБЩАЯ И ЖИЛАЯ ПЛОЩАДЬ?
В жилую площадь частного дома входит площадь комнат для проживания.
Понятие общей площади дома учитывается при расчете нормы, которая должна приходиться на каждого человека, проживающего в данном помещении. И учитывается при расчете необходимой мощности отопительной системы.
Жилая площадь обязательно указывается в объявлениях при продаже, так как этот параметр позволяет оценить реальные размеры жилого пространства. Например, в некоторых проектах в большом доме может быть оборудована просторная прихожая, техпомещение или тамбур, но при этом сами комнаты окажутся маленькими и тесными.
Все эти данные вносятся в технический паспорт дома.
НЮАНСЫ ОЦЕНКИ ОБЩЕЙ И ЖИЛОЙ ПЛОЩАДИ
При расчете общей и жилой площади у покупателя и продавца или у заказчика и застройщика нередко возникают разногласия, так как не учитывается несколько важных нюансов:
- Если в здании есть ниши, высота которых составляет менее 2 м, они не могут учитываться в составе жилой площади помещения. Особенно это важно в так называемых мини-домах.
- Если площадь пространства под лестничным маршем составляет не более полутора метров, она также не будет учитываться при оценке размеров дома.
- Особо сложно рассчитывать размеры жилого помещения мансардного этажа или используемого чердака. В этом случае основным параметров для расчета становится наклон кровли. Если наклон кровли составляет 27 градусов, в общую жилую площадь входит только часть помещения с высотой 1,5 метра до кровли. Подробнее ниже.
Как рассчитать жилую площадь мансардного помещения?
При подсчете площади помещения с наклонным потолком учитывается площадь этого помещения с высотой до наклонного потолка, м:
1,5 — при его наклоне к горизонту 30°;
1,1 — то же 45°;
0,5 — “ 60° и более.
При промежуточных значениях указанного наклона потолка высота определяется по интерполяции. Площадь пола под лестницей учитывается с высотой до ее выступающих конструкций 1,6 м и более. Площадь помещения и пола под лестницей меньшей указанной высоты учитывается в площади помещения с коэффициентом 0,7.
Точный расчет общей и жилой площади необходим при проектировке будущего дома и при последующей приемке здания после завершения строительства. При продаже это один из ключевых параметров, напрямую влияющий на оценку итоговой стоимости здания.
Метки: Информация
Похожие статьи
Ветровая доска
Ветровая доска — защита и украшение дома
Шведский каркасный дом
Шведские каркасные дома — от старинных до современных
Отопление каркасного дома или какой котёл выбрать?
Как правильно выбрать котёл для Вашего дома?
Как рассчитать площадь комнаты, пола, потолка и стен
Обновлено: 02 марта 2021
832427
Затевая ремонт, вы должны приобрести достаточное количество обоев, клея, краски и прочих материалов. Для этого вам необходимо знать, как рассчитать площадь комнаты. Если вы поймете, как получить и применить нужные измерения, то в дальнейшем, например, при покупке или продаже недвижимости, вы сможете самостоятельно посчитать площадь помещения и проверить документы.
Простая комната прямоугольной или квадратной формы
Для того, рассчитать площадь пола комнаты, вы должны определить его форму. В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах.
Формула по которой можно высчитать площадь:
S комнаты = А х B, где A – длина, B – ширина.
Для измерения можно взять обычную рулетку. Чтобы получить наиболее точный результат, рекомендуется измерить длину в начале стены и в конце и, если цифры будут отличаться, взять среднее арифметическое значение.
Комната, в которой имеются ниши или выступы
Если в комнате имеются ниши, выступы, сантехнические или вентиляционные конструкции, то необходимо измерить отдельно площадь каждого участка. Если это ниша в стене, то к площади комнаты нужно прибавить площадь углубления. Если это выступ, то соответственно, из площади помещения нужно будет вычесть его площадь.
Такому же принципу нужно следовать, если вы хотите рассчитать площадь потолка комнаты. Ровный, прямоугольный потолок без каких-либо ниш и выступов означает, что его необходимо измерить по длине и ширине, а затем посчитать площадь простым умножением.
Если вы планируете утеплить пол с помощью нагревательных элементов, то из общей площади пола вам нужно будет вычесть площадь, которая занята тяжелой мебелью.
Комната сложной конфигурации
Нередко встречаются комнаты необычной формы. Если есть возможность, то нужно разделить помещение на несколько прямоугольников, посчитать площадь каждого и сложить.
Площадь комнаты в форме круга вычисляется по формуле:
S комнаты = πR², где R – радиус. Необходимо учитывать, сколько градусов в секторе.
Для расчета площади комнаты треугольной формы используют формулу Герона:
Sкомнаты = √ (P(P -A) х (Р — В) х (Р — С)), где Р – половина периметра треугольника, А, В, С – длины его сторон.
Полупериметр треугольника рассчитываем так: Р = (А + В + С) / 2
Комната со сложной конфигурацией стен. Фото — welovead.com
Особенности расчета площади простых стен и стен, содержащих выступы и ниши
Теперь давайте рассмотрим такой важный момент, как расчет площади стен комнаты. Зная именно эту величину, вы сможете купить нужное количество обоев для ремонта. В этом нет ничего сложного: измерьте длину, ширину и высоту помещения.
Далее площадь стен высчитываем по формуле:
Sстен = Р х С, где Р – периметр комнаты, С – высота стен.
Периметр комнаты считаем по формуле:
Р = (А + В) х 2, где A – длина, B – ширина.
Для получения более точных результатов, из общей площади стен необходимо вычесть площадь дверных и оконных проемов.
Площадь стен комнаты с выступами или углублениями будет отличаться от площади стен простой комнаты. Не забудьте к основному значению прибавить площадь стены выступающего или углубленного участка.
Будьте внимательны, производя измерения и расчеты. Если вы используете лазерную рулетку, то следите за тем, чтобы луч был направлен строго перпендикулярно стене, иначе вы получите большую погрешность в результатах.
Стены комнаты с выступами. Фото — gohawaii.about.com
Если вы заметили ошибку, не рабочее видео или ссылку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Калькулятор объема
. Определение | Формулы
Калькулятор объема вычислит объем некоторых из наиболее распространенных трехмерных твердых тел. Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемого двухмерной фигурой. Поэтому вы можете быть сбиты с толку относительно того, как найти объем прямоугольника по сравнению с тем, как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.
Что такое объем? Определение объема
Объем — это объем пространства, занимаемого объектом или веществом. Как правило, под объемом контейнера понимается его вместимость, а не пространство, которое сам контейнер перемещает. Кубический метр (м 3 ) — это единица измерения объема в системе СИ.
Однако термин том может также относиться ко многим другим вещам, например,
- степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
- количество или количество чего-либо (обычно большого количества)
- формальное слово для книга или одна из набора связанных книг.
Единицы объема, таблица пересчета
Популярные единицы объема:
- Метрические единицы объема
- кубических сантиметров (см³)
- кубических метров (м³)
- литров (л, л)
- миллилитры (мл, мл)
- Стандарт США, Великобритания
- жидкая унция (жидкая унция)
- кубических дюймов (у.е.)
- кубических футов
- стаканов
- пинт (пт)
- кварты (кварты)
- галлонов (гал.)
Если вам нужно преобразовать единицы объема, вы можете использовать наш конвертер больших объемов.Еще один полезный инструмент — наш калькулятор граммов в чашки, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммов) к единице объема (чашки) — поэтому вам нужно знать тип ингредиента (или, точнее, его плотность).
Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:
| кубических дюймов | кубических футов | кубических ярдов | галлонов сша | галлонов сша | imp жидких галлонов | баррелей (нефть) | стаканов | жидких унций (Великобритания) | жидких унций (США) | пинт (Великобритания) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| куб.м | 6.1 10 4 | 35,3 | 1,30 8 | 264,2 | 227 | 220 | 6,29 | 4227 | 3,52 10 4 | 3,38 10 4 | 1760 |
| кубический дециметр | 61.02 | 0,035 | 1,3 10 -3 | 0,264 | 0,227 | 0,22 | 0,006 | 4,23 | 35,2 | 33,8 | 1,76 |
| кубический сантиметр | 0.061 | 3,5 10 -5 | 1,3 10 -6 | 2,64 10 -4 | 2,27 10 -4 | 2,2 10 -4 | 6,29 10 -6 | 4,2 10 -3 | 3,5 10 -2 | 3.34 10 -2 | 1,76 10 3 |
| кубический миллиметр | 6,1 10 -5 | 3,5 10 -8 | 1,31 10 -9 | 2,64 10 -7 | 2,27 10 -7 | 2,2 10 -7 | 6.3 10 -9 | 4,2 10 -6 | 3,5 10 -5 | 3,4 10 -5 | 1,76 10 -6 |
| гектолитра | 6,1 10 3 | 3,53 | 0,13 | 26.4 | 22,7 | 22 | 0,63 | 423 | 3,5 10 3 | 3381 | 176 |
| литра | 61 | 3,5 10 -2 | 1.3 10 -3 | 0,26 | 0,23 | 0,22 | 6,3 10 -3 | 4,2 | 35,2 | 33,8 | 1,76 |
| сантилитра | 0,61 | 3.5 10 -4 | 1,3 10 -5 | 2,6 10 -3 | 2,3 10 -3 | 2,2 10 -3 | 6,3 10 -5 | 4,2 10 -2 | 0,35 | 0,338 | 1.76 10 -2 |
| миллилитры | 6,1 10 -2 | 3,5 10 -5 | 1,3 10 -6 | 2,6 10 -4 | 2,3 10 -4 | 2,2 10 -4 | 6,3 10 -6 | 4.2 10 -3 | 3,5 10 -2 | 3,4 10 -2 | 1,76 10 -3 |
| кубические дюймы | 1 | 5,79 10 -4 | 2,1 10 -5 | 4,3 10 -3 | 3.7 10 -3 | 3,6 10 -3 | 10 -4 | 6,9 10 -2 | 0,58 | 0,55 | 2,9 10 -2 |
| кубических футов | 1728 | 1 | 0.037 | 7,48 | 6,43 | 6,23 | 0,18 | 119,7 | 997 | 958 | 49,8 |
| кубических ярдов | 4,7 10 4 | 27 | 1 | 202 | 173.6 | 168,2 | 4,8 | 3232 | 2,69 10 4 | 2,59 10 4 | 1345 |
| галлон жидкого топлива сша | 231 | 0,134 | 4,95 10 -3 | 1 | 0.86 | 0,83 | 0,024 | 16 | 133,2 | 128 | 6,7 |
| сухих галлонов сша | 268,8 | 0,156 | 5,76 10 -3 | 1.16 | 1 | 0,97 | 0,028 | 18,62 | 155 | 148,9 | 7,75 |
| imp жидкие галлоны | 277,4 | 0,16 | 5,9 10 -3 | 1.2 | 1,03 | 1 | 0,029 | 19,2 | 160 | 153,7 | 8 |
| баррелей (нефть) | 9702 | 5,61 | 0,21 | 42 | 36.1 | 35 | 1 | 672 | 5596 | 5376 | 279,8 |
| чашки | 14,4 | 8,4 10 -3 | 3,1 10 -4 | 6.2 10 -2 | 5,4 10 -2 | 5,2 10 -2 | 1,5 10 -3 | 1 | 8,3 | 8 | 0,4 |
| жидких унций (Великобритания) | 1,73 | 10-3 | 3.7 10 -5 | 7,5 10 -3 | 6,45 10 -3 | 6,25 10 -3 | 1,79 10 -4 | 0,12 | 1 | 0,96 | 5 10 -2 |
| жидких унций (США) | 1.8 | 10 -3 | 3,87 10 -5 | 7,8 10 -3 | 6,7 10 -3 | 6,5 10 -3 | 1,89 10 -4 | 0,13 | 1,04 | 1 | 0.052 |
| пинты (Великобритания) | 34,7 | 0,02 | 7,4 10 -4 | 0,15 | 0,129 | 0,125 | 3,57 10 3 | 2,4 | 20 | 19.2 | 1 |
Как рассчитать объем? Формулы объема
На этот вопрос нет однозначного ответа, так как он зависит от формы рассматриваемого объекта. Вот формулы для некоторых из наиболее распространенных форм:
Куб =
с³, где с — длина стороны.Сфера =
(4/3) πr³, где r — радиус.Цилиндр =
πr²h, где r — радиус, а h — высота.Конус =
(1/3) πr²h, где r — радиус, а h — высота.Прямоугольное тело (объем ящика) =
lwh, где l — длина, w — ширина и h — высота (примером такой формы может служить простой бассейн).Пирамида =
(1/3) Ah, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием также можно использовать другое уравнение: Пирамида =(n / 12) * h * длина_сокры ² * кроватка (π / n), где n — количество сторон основания для правильный многоугольник.Призма =
πAh, где A — площадь основания, а h — высота. Для прямоугольной призмы уравнение можно легко вывести, как и для правой прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и прямоугольник.
| Форма | Имя | Формула |
|---|---|---|
| Куб | В = с³ | |
| Призма прямоугольная правая (прямоугольная, прямоугольная) | V = lwh | |
| Призма или цилиндр | В = Ач | |
| Пирамида или конус | В = Ач / 3 | |
| Сфера | V = 4πr³ / 3 |
Калькулятор объема и инструменты, предназначенные для определенных форм
Мы решили сделать из этого калькулятора объема простой инструмент, охватывающий пять самых популярных трехмерных фигур.Однако не все уравнения объема и формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и не интуитивно понятным. Так что, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных форм:
Калькулятор объема
— как использовать
Давайте посмотрим на примере использования этого калькулятора объема:
Выберите тип 3D-формы . Если вы не можете найти форму, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше).В этом примере предположим, что вы хотите рассчитать объем цилиндра.
Выберите правый раздел калькулятора объема . В нашем случае это деталь под названием Объем цилиндра .
Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения простым щелчком по названию единицы.
Поехали! Отображается объем выбранной формы .В нашем случае это 9,42478 куб. Футов
Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите бочки из раскрывающегося списка. Наш цилиндр имеет емкость ~ 2,24 баррелей масла.
Измерение объема твердых тел, жидкостей и газов
Как найти объем объектов с разным состоянием материи?
- Цельный
Для обычных трехмерных объектов вы можете легко вычислить объем, измерив его размеры и применив соответствующее уравнение объема.Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иеро из чистого золота или просто позолочена, но не сгибая и не разрушая ее. Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил в воду.Зная объем необычного объекта и его вес, он мог вычислить плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.
Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите емкость больше, чем объект, объем которого вы хотите измерить, .Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала.
Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь . Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между измерениями — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
- Жидкость
Обычно измерить объем жидкости довольно просто — все, что вам нужно, это какой-нибудь мерный сосуд с градуировкой. Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Емкости, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от тех, которые используются в химии (например.грамм. в расчетах молярной концентрации) будет отличаться от тех, которые используются в медицинских целях (например, доза лекарства).
- Газ
Мы должны использовать более сложные методы для измерения объема газа. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Надуйте баллон газом, который вы хотите измерить (например,г., с гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.
Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа , учитывая его плотность и массу . Используйте простое уравнение объема
V = m / d.Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
Как найти объем * прямоугольника * по сравнению с объемом * коробки *
Вы не можете рассчитать объем прямоугольника , объем круга или объем квадрата, потому что это двухмерные геометрические фигуры.Таким образом, прямоугольник не имеет объема (но имеет площадь). Вероятно, вы ищете объем прямоугольного кубоида (или, говоря более общим языком, вы хотите найти объем коробки), который представляет собой трехмерный объект.
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если размер коробки 5х7х2 см, то объем коробки составляет 70 кубических сантиметров.
Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную.Для больших или десятичных чисел использование калькулятора объема очень эффективно.
В реальной жизни есть много приложений, в которых может пригодиться калькулятор объема. Один из таких примеров — строительство дорог или тротуаров, где должны быть построены бетонные плиты. Как правило, бетонные плиты представляют собой твердые тела прямоугольной формы, поэтому можно использовать калькулятор бетона, который является приложением калькулятора объема.
Также формулы объема могут быть полезны, если вы увлеченный садовник или просто счастливый обладатель дома с двором.Ознакомьтесь с нашими замечательными инструментами, такими как:
Более того, вы можете встретить volume на своей кухне или в ванной: у любой жидкости, которую мы пьем (например, воды в бутылках), а также косметических товаров или зубной пасты на упаковке продукта указан объем (в миллилитрах / литрах или жидких унциях). / галлоны).
Еще одно родственное приложение, хотя и немного другое, — это концепция площади поверхности. Предположим, что весь фасад здания должен быть окрашен. Чтобы знать, сколько нужно купить краски, необходимо рассчитать площадь здания.Удобный в использовании калькулятор площади рассчитает это за вас.
FAQ
Как найти объем?
Формула объема зависит от формы объекта . Одной из самых популярных форм является прямоугольная призма, также известная как коробка, где вы можете просто умножить длину на ширину на высоту , чтобы найти ее объем. Другой распространенной формой является цилиндр — чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π ⨉ r 2 ).Для других трехмерных фигур проверьте Калькулятор объема Omni.
Как измерить объем?
Измерение объема зависит от состояния вещества вашего объекта. Для жидкостей вы можете использовать мерный цилиндр или бюретку для измерений в химической лаборатории или мерный стакан и ложку для повседневных целей. Что касается газов, чтобы приблизительно измерить объем, вы можете надуть баллон и использовать его для вытеснения воды в мерном цилиндре. Аналогичный метод работает для твердых тел — поместите объект в градуированный контейнер и измерьте изменение показаний.
Объем — квадрат или куб?
Объем «кубический», так как это трехмерная мера. Площадь — это «квадратное» значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой кубическое значение, вспомнив несколько названий единиц объема, например, кубических метров , кубических футов или кубических ярдов .
Как рассчитать объем?
В зависимости от формы объекта вы можете использовать разные формулы для расчета объема:
- Объем куба = сторона 3 .
- Кубоид (прямоугольная коробка) объем = длина ⨉ ширина ⨉ высота
- Объем сферы = (4/3) ⨉ π ⨉ радиус 3
- Объем цилиндра = π ⨉ радиус 2 ⨉ высота
- Объем конуса = (1/3) ⨉ π ⨉ радиус 2 ⨉ высота
- Объем пирамиды = (1/3) площадь основания ⨉ высота
В чем измеряется объем?
Кубический метр — единица объема в системе СИ.Однако, поскольку это непрактично, чаще всего вы можете встретить объем, выраженный в:
.
- Кубические сантиметры
- Кубические дюймы
- Миллилитры
- литров
- галлонов
Как найти объем жидкости?
Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку.Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы измерения объема, вы можете просто использовать мерный стакан, стакан или ложку.
Что такое единица СИ для объема?
Кубический метр (м 3 ) — это единица измерения объема в системе СИ. Он образован от основной единицы длины в системе СИ — метра. Хотя кубический метр является основной единицей СИ, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, а для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах и т. Д. кубические футы или кубические ярды.
Является ли объем интенсивным или обширным?
Объем — это обширное свойство , такое же, как количество вещества, массы, энергии или энтропии. Обширное свойство — это мера, в которой зависит от количества вещества . Посмотрите на этот пример: стакан, бочка и бассейн, полный воды, имеют разные объем и массу ( обширных свойств ), но вода в этих трех контейнерах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивных свойств ). ).
В чем разница между площадью поверхности и объемом?
Объем — это трехмерная мера , а площадь поверхности — двумерная . Объем сообщает нам о кубическом пространстве, которое занимает объект, а площадь поверхности — это сумма всех областей, образующих трехмерную форму. Возьмем, например, картонную коробку 📦:
- Объем — это объем места, занимаемого коробкой, просто это свободного места внутри коробки
- Площадь поверхности — это пространство , занимаемое сторонами коробки , вычисленное при покраске сторон или упаковке коробки в бумагу.
Как найти объем объекта неправильной формы?
Вы можете использовать метод вытеснения жидкости для твердых объектов неправильной формы:
- Наполните емкость водой и отметьте уровень воды.
- Бросьте ваш объект внутрь и снова отметьте уровень. Убедитесь, что ваш объект не растворяется в воде.
- Для масштабированных контейнеров вы можете всего вычесть исходного объема из нового объема. И все, поздравляю!
Но если на вашем оригинальном контейнере нет весов:
- Вынести предмет.
- Заполните вашу емкость водой до второй отметки, залейте этой воды в мерный цилиндр / другую мерную емкость.
- Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.
- Пат себе на спину — вы нашли объем объекта неправильной формы!
Что измеряет объем?
Объем измеряет объем пространства, занимаемого объектом в трех измерениях .Еще один близкий термин — вместимость, то есть объем внутреннего пространства объекта. Другими словами, вместимость описывает, сколько контейнер может вместить (воды, газа и т. Д.).
Каков объем Земли?
Объем Земли примерно равен 1,08321 × 10 12 км 3 ( 1,08 квадриллион кубических километров ), или 2,59876 × 10 11 кубических миль ( 259 триллионов кубических миль ). Вы можете получить этот результат, используя формулу объема сферы (4/3) ⨉ π ⨉ radius 3 и предполагая, что средний радиус Земли составляет 6371 километр (3958.76 миль).
Как рассчитать отношение площади поверхности к объему?
Чтобы рассчитать отношение площади поверхности к объему SA: V, вы просто разделите площадь поверхности на объема. Для некоторых выбранных форм:
- Соотношение SA: V для куба = (сторона 6 ⨉ 2 ) / (сторона 3 ) = 6 / сторона
- Отношение SA: V для сферы = (4 ⨉ π ⨉ радиус 2 ) / ((4/3) ⨉ π ⨉ радиус 3 ) = 3 / радиус
- Соотношение SA: V для цилиндра = (2 ⨉ π ⨉ радиус 2 + 2 ⨉ π ⨉ радиус ⨉ высота) / (π ⨉ радиус 2 ⨉ высота) = 2 ⨉ (радиус + высота) / ( радиус ⨉ высота)
Как рассчитать объем
Расчет объема
Объем измеряется в кубах (или кубических единицах).
Сколько кубиков в этой прямоугольной призме (кубоиде)?
Мы можем считать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.
Объем прямоугольной призмы = длина x ширина x высота
Примеры расчета площади прямоугольника
Нам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту.Примеры ниже показывают, как это можно сделать тремя способами.
Обратите внимание, как мы получаем один и тот же ответ независимо от того, какой стороной мы находим область.
Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно работает с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге как плоские — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения. Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, как о еще одной «фигуре на странице».«Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что на бумаге, и тем, что она представляет в реальном мире.
Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.
Единицы измерения объема
Есть очень большие различия между единицами измерения объема. Например, в 1 метре 100 сантиметров, а в кубическом метре 1000000 (да, 1 миллион) кубических сантиметров.
Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.
Сколько сахара? 1 м 3 или 1000000 см 3
Подумайте о наполнении очень большой коробки (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).
| Шаг 1: один ряд вдоль дна коробки — , что составляет 100 кубиков сахара | |
| Шаг 2: накройте оставшуюся часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиками сахара в каждом.100 x 100 = 10000 сахара кубик на дне большой коробки. | |
| Шаг 3: Повторите это 99 раз, пока не получите слой из 10 000 кубов, уложенных стопкой в 100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара |
1000000 см 3 в 1 м 3 — будьте осторожны, чтобы не было слишком много сахара!
Есть и другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.
| Не забывайте крошечный 3 |
| Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Пишем мм 3 , см 3 , м 3 , км 3 , см 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров» |
Примеры расчета объема прямоугольных призм
| Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3 | |
| Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3 | |
| Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3 |
Объем цилиндра
Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра.Основание цилиндра круглое, а формула площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
| Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h |
Примечание: в приведенных ниже примерах мы будем использовать 3,14 в качестве приблизительного значения для π (Pi).
Пример расчета объема цилиндра
| Размеры указаны в см. | Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3 |
Объем конуса
Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.
| Объем = 1/3 πr 2 ч |
Пример расчета объема конуса
| Размеры указаны в см. | Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3 |
Объем сферы
Формула объема шара приведена ниже.
| Объем = 4/3 πr 3 |
Пример расчета объема сферы
| Размеры указаны в см. | Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3 |
Рабочие листы для печати
Используйте таблицу ниже, чтобы попрактиковаться в вычислении объемов.
Вы можете получить другие рабочие листы геометрии по периметру, площади и т. Д. Здесь.
Как рассчитать площадь, периметр и объем
Обновлено 16 декабря 2020 г.
Сара Селеби
Измерение площади, периметра и объема имеет решающее значение для строительных проектов, ремесел и других приложений.
Площадь — это пространство внутри границы двухмерной формы. Периметр — это расстояние вокруг двухмерной фигуры, например квадрата или круга. Объем — это мера трехмерного пространства, занимаемого объектом, например кубом. Если вы знаете размеры объекта, то легко измерить площадь и объем.
Формулы площади поверхности и объема для всех повседневных геометрических фигур можно легко найти в Интернете, хотя неплохо было бы рассмотреть, как получить их самостоятельно, если возникнет такая необходимость.Вы также можете часто получить одно из них от другого; например, если вы знаете формулу для площади круга, вы можете вычислить, что объем цилиндра — это просто площадь соответствующего круга (ов) в конце, умноженная на высоту цилиндра.
Как рассчитать площадь квадрата или прямоугольника
Запишите длину ( l ) и ширину ( w ) квадрата или прямоугольника. Подставьте свои измерения в формулу
A = l \ times w
, чтобы найти площадь ( A ).2
Площадь ( A ) круга радиусом 5 дюймов составляет 78,5 квадратных дюймов.
Периметр квадрата, прямоугольника или треугольника
Запишите длины всех сторон квадрата, прямоугольника или треугольника.
Добавьте размеры, чтобы получить значение периметра ( P ). Например, прямоугольный сад размером 5 на 7 метров имеет две стороны размером 5 метров и две стороны размером 7 метров. Периметр ( P ):
P = 5 + 5 + 7 + 7 = 24 \ text {meter}
Периметр прямоугольного сада составляет 24 метра. 3
Размер коробки составляет 15 кубических футов.3
Объем цилиндра 62,8 кубических метра или 62,8 кубических метра.
Расчет площади, периметра и объема
Расчет площади, периметра и объема простых геометрических фигур можно найти, применив некоторые основные формулы. Хорошая идея — изучить и понять, что это такое, и сохранить эти формулы в памяти.
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
Калькулятор объема конической усадки
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема трубки
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр, или м 3 . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус формируется аналогично окружности набором отрезков прямой, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, не зря потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что он должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно построил замок из песка в своем доме и в качестве дополнительного бонуса ему удалось сэкономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный резервуар
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, несмотря на то, что она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + в) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может нести в капсуле времени, которую он хочет похоронить для будущих поколений на своем пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Имея два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
Для R и h : r = √2Rh — h 2
где r — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую Джек срезал, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая усадка
Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
.
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би есть усеченная пирамида правой конической формы, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 из 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки линии, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямых линий. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
, где b — площадь основания, а h — высота
.
Объем квадратной пирамиды:
, где a — длина края основания
EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами.Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, и его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
, где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубки
EX: Beulah посвящен охране окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу через ручей. Он хочет облегчить доступ к своему дому и просит Беулу построить ему дорогу, следя за тем, чтобы ручей мог течь свободно, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые дамбы будут хорошей отправной точкой для прокладки трубы через ручей. Объем запатентованного бетона с низкой ударопрочностью, необходимый для строительства трубы с внешним диаметром 3 фута и внутренним диаметром 2.5 футов и длина 10 футов можно рассчитать следующим образом:
| объем = π × | × l0 = 21,6 футов 3 |
Единицы измерения общего объема
| Единица | кубических метров | миллилитров | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| миллилитров (кубических сантиметров) | 0,000001 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кубических дюймов | 0,00001639 | 000473 | 473 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кварта | 0,000946 | 946 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| литр | 0,001 | 1,000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| галлон | 0,00103,7103 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кубический ярд | 0,764555 | 764,555 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кубический метр | 1 | 1,000,000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кубический километр | 1,000,000,000 |
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и пометьте его данной информацией. |
| 1. | |
| Шаг 2. Определите , что вы ищете. | объем прямоугольный сплошной |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть [латекс] V [/ латекс] = объем |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | [латекс] V = LWH [/ латекс] [латекс] V = \ mathrm {14} \ cdot 9 \ cdot 17 [/ латекс] |
| Шаг 5. Решите уравнение. | [латекс] V = 2,142 [/ латекс] |
| Шаг 6. Чек Мы предоставляем вам проверить свои расчеты. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс] \ text {1,034} [/ латекс] квадратных сантиметров. |
| 2. | |
| Шаг 2. Определите , что вы ищете. | площадь поверхности твердого тела |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть [латекс] S [/ латекс] = площадь поверхности |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | [латекс] S = 2LH + 2LW + 2WH [/ латекс] [латекс] S = 2 \ left (14 \ cdot 17 \ right) +2 \ left (14 \ cdot 9 \ right) +2 \ left (9 \ cdot 17 \ right) [/ latex] |
| Шаг 5. Решите уравнение. | [латекс] S = 1,034 [/ латекс] |
| Шаг 6. Проверка: Перепроверьте с помощью калькулятора. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс] 1034 [/ латекс] квадратных сантиметров. |
пример
Прямоугольный ящик имеет длину [латекс] 30 [/ латекс] дюймов, ширину [латекс] 25 [/ латекс] дюймов и высоту [латекс] 20 [/ латекс] дюймов.Найдите его 1. объем и 2. площадь поверхности.
Показать решение
Решение
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз.
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и пометьте его данной информацией. |
| 1. | |
| Шаг 2. Определите , что вы ищете. | объем ящика |
| Шаг 3. Имя. Выберите переменную для ее представления. | let [латекс] V [/ latex] = объем |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | [латекс] V = LWH [/ латекс] [латекс] V = 30 \ cdot 25 \ cdot 20 [/ латекс] |
| Шаг 5. Решите уравнение. | [латекс] V = 15 000 [/ латекс] |
| Шаг 6. Проверка: Еще раз проверьте свои математические расчеты. | |
| Шаг 7. Ответьте на вопрос. | Объем [латекс] 15 000 [/ латекс] кубических дюймов. |
| 2. | ||||||||||||||||||||||||||||||||||||||
| Шаг 2. Определите , что вы ищете. | площадь ящика | |||||||||||||||||||||||||||||||||||||
Шаг 3. {2} [/ latex].Объем и площадь кубаДля любого куба со сторонами длиной [латекс] с [/ латекс], примерКуб [латекс] 2,5 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности. Решение
примерКубик блокнота размером [латекс] 2 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности. Показать решение Решение
Объем куба | Формула и как найти (видео)Объем кубаОбъем куба — это то, сколько места занимает куб в трех измерениях.Вы можете найти объем любого куба с одним заданным измерением, используя формулу объема куба : Объем куба всегда измеряется в кубических единицах, производных от линейных единиц, заданных или используемых для измерения длины стороны. Содержание
Что такое куб?Куб представляет собой трехмерное тело с шестью конгруэнтными квадратными гранями, пересекающимися под прямым углом, восемью вершинами и двенадцатью сторонами равной длины.Куб — одно из пяти Платоновых Тел, его также называют шестигранником. Каковы размеры куба?Куб — это трехмерный объект, поэтому куб имеет три измерения:
Обратите внимание, у нас есть два способа описать третье измерение:
Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба. Формула объема кубаОбъем формулы куба — это объем, равный длине, умноженной на ширину, умноженной на высоту. Это уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и кубоидов. Поскольку все три значения — l, w и h — одинаковы в кубе, простейший объем формулы куба: В этом объеме уравнения куба s = длина любого ребра. Объем всегда измеряется в кубических единицах на основе предоставленных вам линейных единиц. Если вам говорят, что край куба составляет 3 метра, объем измеряется в кубических метрах или м3 (кубических метрах). Как найти объем кубаЧтобы найти объем куба, вам нужно знать только длину любого ребра. Если вам дана длина одной стороны, вы можете найти объем куба, подставив его в одну из формул объема для куба:
Чтобы измерить пространство, занимаемое кубом, нужно знать длину любого ребра, потому что все стороны куба равны по длине. Как определить длину, ширину и высоту по объемуЧто делать, если вам дан объем куба и попросят найти размеры куба? Если вам дан объем куба и попросят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема: Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах. Что делать, если у нас есть куб, и нам говорят, что его объем составляет 729 кубических метров. Чтобы найти длину ребра куба: с = 729 м33 s = 9 метров Как рассчитать объем по площадиВот еще одна проблема. Что, если вам сообщат область одной грани куба? Можете ли вы использовать эту информацию, чтобы найти объем? Да, площадь одного лица равна длине лица, умноженной на ширину.Как только вы найдете ширину или длину, вы можете применить формулу объема:
Как рассчитать площадь поверхности куба, используя объемЕсли вам дан объем куба, вы можете преобразовать его в длину одной стороны. Затем вы можете использовать длину стороны для расчета общей площади поверхности. Используйте длину ребра, чтобы вычислить площадь поверхности одной стороны, затем умножьте эту площадь на 6. Это даст вам общую площадь поверхности куба с учетом объема. Что, если вам скажут, что общая площадь поверхности всего куба ? Вы можете найти объем? Да, общая площадь поверхности складывается из площади всех шести совпадающих граней. Найдите область одного лица, а затем выполните шаги, описанные выше, чтобы найти объем:
Примеры объема кубаЕсли у вас есть трехмерное твердое тело с шестью гранями, стороны которого обозначены как 4 ‘, 6’ и 8 ‘.Это куб? Нет, это прямоугольная призма, потому что метки, которые превосходят рисунок, имеют разную длину! Что, если бы стороны нашего твердого тела были 4 ‘, 4’ и 4 ‘; это куб? Это куб, потому что на этикетках указано, что ширина, длина и высота одинаковы. |

 Измеряем каждую в отдельности, считаем объем для частей и складываем результаты. Понятно, что такой результат будет не очень точным. И, чем сложнее предмет, тем больше ошибка.
Измеряем каждую в отдельности, считаем объем для частей и складываем результаты. Понятно, что такой результат будет не очень точным. И, чем сложнее предмет, тем больше ошибка.