Расчет сопротивления цепи
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
R4=20 Ом, R5=40 Ом, R6=15 Ом
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
10 лучших бесплатных онлайн симуляторов электроцепи
РадиоКот >Чердак >
10 лучших бесплатных онлайн симуляторов электроцепи
Список бесплатных программ моделирования электронной цепи онлайн очень полезный для вас. Эти симуляторы электроцепи, которые я предлагаю, не нужно быть загружен в компьютере, и они могут работать непосредственно с веб-сайта.
1. EasyEDA дизайн электронной цепи, моделирование цепи и PCB дизай:
EasyEDA удивительный бесплатный онлайн симулятор электроцепи, который очень подходит для тех, кто любит электронную схему. EasyEDA команда стремится делать сложную программу дизайна на веб-платформе в течение нескольких лет, и теперь инструмент становится замечательным для пользователей. Программная среда позволяет тебя сам проектировать схему. Проверить операцию через симулятор электроцепи. Когда вы убедитесь функцию цепи хорошо, вы будете создавать печатную плату с тем же программным обеспечением. Есть более 70,000+ доступных диаграмм в их веб-базах данных вместе с 15,000+ Pspice программами библиотеки. На сайте вы можете найти и использовать множество проектов и электронных схем, сделанные другими, потому что они являются публичными и открытыми аппаратными оснащениями. Он имеет некоторые довольно впечатляющие варианты импорта (и экспорта). Например, вы можете импортировать файлы в Eagle, Kikad, LTspice и Altium проектант, и экспортировать файлы в .PNG или .SVG. Есть много примеров на сайте и полезных программ обучения, которые позволяют людей легко управлять.
Когда вы убедитесь функцию цепи хорошо, вы будете создавать печатную плату с тем же программным обеспечением. Есть более 70,000+ доступных диаграмм в их веб-базах данных вместе с 15,000+ Pspice программами библиотеки. На сайте вы можете найти и использовать множество проектов и электронных схем, сделанные другими, потому что они являются публичными и открытыми аппаратными оснащениями. Он имеет некоторые довольно впечатляющие варианты импорта (и экспорта). Например, вы можете импортировать файлы в Eagle, Kikad, LTspice и Altium проектант, и экспортировать файлы в .PNG или .SVG. Есть много примеров на сайте и полезных программ обучения, которые позволяют людей легко управлять.
2. Circuit Sims: Это был один из первых вебов исходя из эмуляторов электроцепи с открытым кодом я тестировал несколько лет назад. Разработчик не удалось повысить качество и увеличить графический интерфейс пользователя.
3. DcAcLab имеет визуальные и привлекательные графики, но ограничивается моделированием цепи. Это несомненно отличная программа для обучения, очень проста в использовании. Это делает вас видеть компоненты, как они сделаны. Это не позволит вам проектировать схему, но только позволит сделать практику.
Это несомненно отличная программа для обучения, очень проста в использовании. Это делает вас видеть компоненты, как они сделаны. Это не позволит вам проектировать схему, но только позволит сделать практику.
4. EveryCircuit представляет собой электронный эмулятор онлайн с хорошими сделанными графиками. Когда вы входите в онлайн программу, и она будет просить вас создать бесплатный счет, чтобы вы можете сохранить ваши проекты и иметь ограниченную часть площади рисовать вашу схему. Чтобы использовать его без ограничений, требующих годовой взнос в размере $ 10. Он можно скачивать и использоваться на платформах Android и iTunes. Компоненты имеют ограниченную способность имитировать с небольшими минимальными параметрами. Очень просто в использовании, он имеет прекрасную систему электронного дизайна. Она позволяет вам включать (вставлять) моделирование в ваши веб-страницы.
5. DoCircuits: Хотя она оставляет людям первое впечатление от путаницы о сайте, но она дает много примеров о том, как работает программа, можно видеть себя на видео «будет начать в пять минут». Измерения параметров электронной схемы продемонстрируют с реалистичными виртуальными инструментами.
Измерения параметров электронной схемы продемонстрируют с реалистичными виртуальными инструментами.
6. PartSim электронный симулятор схемы онлайн. Он был способным к моделированию. Вы можете рисовать электрические схемы и протестировать их. Он еще новый симулятор, так что есть несколько компонентов, чтобы сделать моделирования для выбора.
7. 123D Circuits Активная программа разработана AutoDesk, она позволяет вам создавать схему, можно увидеть её на макетной плате, использовать платформу Arduino, имитировать электронную схему и окончательно создать PCB. Компоненты продемонстрируются в 3D в их реальной форме. Вы можете запрограммировать Arduino непосредственно из этой программы моделирования, (она) действительно производит глубокое впечатление.
8. TinaCloud Эта программа моделирования имеет усовершенствованные возможности. Она позволяет вам моделировать, в дополнение к обычным схемам со смешанными сигналами, и микропроцессорами, VHDL, SMPS поставки электричества и радио частотных цепей. Расчеты для электронного моделирования выполняются непосредственно на сервере компании и позволяют отличную скорость моделирования
Расчеты для электронного моделирования выполняются непосредственно на сервере компании и позволяют отличную скорость моделирования
9.Spicy schematics является программой формы cross-plat, все формы платформы можно поддерживать, в том числе iPad.
10. Gecko simulations представляют собой программы моделирования, специализирующаяся на открытый код и питания цепей. С помощью этой программы вы также можете проверить способность тепловой энергии схемы. Это программа является отпочкованием ETH (ETH Zurich).
Файлы:
Документ MS Word
Документ MS Word
Все вопросы в
Форум.
Как вам эта статья? | Заработало ли это устройство у вас? |
правила расчета для определения силы тока
На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Пример сложных электрических цепей
Пути вычисления электрических схем
Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.
Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.
Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.
Все элементы и устройства подразделяются на три категории:
- Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую.
 Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения; - Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
- Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.
Также к основным понятиям электрической схемы относятся:
- Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
- Узел электрической схемы – точка соединения трех и более ветвей схемы;
- Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.

Обозначение ветвей, узлов и контуров на схеме
Метод расчета по законам Ома и Кирхгофа
Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.
Закон Ома для участка цепи
По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:
UR=RI.
Исходя из этой формулы, найти силу тока можно по выражению:
I=UR/R, где:
- UR – напряжение или падение напряжения на резисторе;
- I – ток в резисторе.
Закон Ома для полной цепи
В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:
I=E/Rэ = E/r0+R, где:
- E – ЭДС источника питания;
- rо – внутреннее сопротивление источника питания.
Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.
Первый закон Кирхгофа
Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:
∑mIk=0, где m – число ветвей, подведенных к узлу.
Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».
Второй закон Кирхгофа
Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:
∑nEk=∑mRkIk=∑mUk, где:
- n – число источников ЭДС в контуре;
- m – число элементов с сопротивлением Rk в контуре;
- Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.
Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:
- Указать относительно положительные направления ЭДС, токов и напряжений;
- Указать направление обхода контура, описываемого уравнением;
- Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.

Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:
∑EI=∑RI2.
Метод преобразования электрической цепи
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.
Последовательное и параллельное соединение элементов
Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
- R1=R12R31/R12+R31+R23,
- R2=R12R23/R12+R31+R23,
- R3=R31R23/R12+R31+R23.
Треугольник и звезда соединений
Дополнительные методы расчета цепей
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.

Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Видео
Оцените статью:
Расчёт электрической цепи постоянного тока методом узловых и контурных уравнений.
Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.
Порядок расчёта:
1. Произвольно задаёмся направлением токов в ветвях.
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.
Красным выделены изменения после первого действия
Синим выделены изменения после третьего пункта
2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:
- Обозначаем узлы буквами.
- Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
0=I1-I4-I6 (Полученное уравнение) - Повторяем пункт B ещё для двух узлов.
0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы.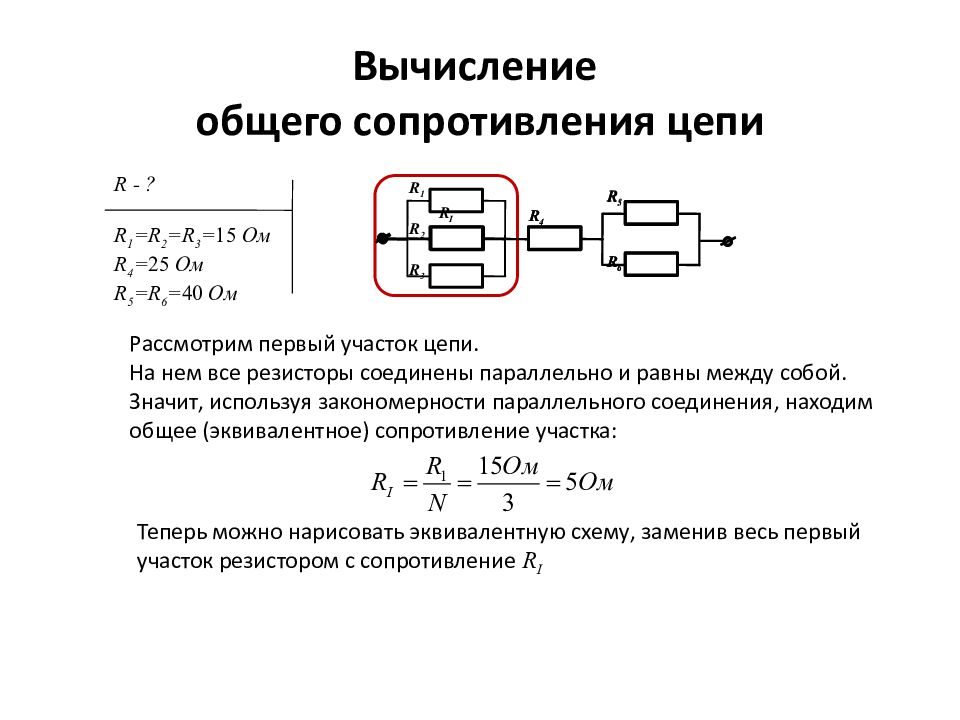 Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.
Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.
3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)
3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)
3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.
Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3
Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5
Контур ABCA 0=I6*R6-I4*R4+I5*R5
4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.
Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.
0=I1-I4-I6 (Узел А)
0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.
I6=I1-I4(Узел А)
I3=I1+I2(Узел D)
I5=I3-I4(Узел В)
I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:
I5=I1+I2-I4
Заменим токи I3 I5 I6 и получим уравнения с тремя токами :
E1=I1*(R1+R01)+I4*R4+(I1+I2)*R3
E2=I2*(R2+R02)+(I1+I2)*R3+(I1+I2-I4)*R5
0=(I1-I4)*R6-I4*R4+(I1+I2-I4)*R5
Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:
40 = 71*I1 + 24*I2 + 14*I4
20 = 55*I1 + 93*I2 — 61*I4
0 = 60*I1 + 16*I2 — 81*I4
Дальше для решения системы можно воспользоваться бесплатной онлайн программой на нашем сайте.
Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.
Правильность решения можно проверить с помощью баланса мощностей.
Расчёт электрических цепей онлайн
Расчёт электрических цепей онлайн
☰
Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей происходит пересчёт результата.
Расчёт реактивного сопротивления конденсатора C и катушки L
Реактивное сопротивление ёмкости | Реактивное сопротивление индуктивности |
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Параллельное соединение двух сопротивлений | Последовательное соединение двух ёмкостей |
Расчёт резистивного и ёмкостного делителей
Расчёт резистивного делителя напряжения | Расчёт ёмкостного делителя напряжения |
Расчёт частоты колебательного контура и цепочки RC
Частота резонанса колебательного контура LC | Пост. |
Компенсация реактивной мощности
Реактивная мощность Q = √((UI)²-P²) |
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
После сброса ввести два любых известных параметра I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; |
Теория, расчёты и справочные материалы
Параметры синусоидального тока,
Справочные данные диодов,
Стабилитроны. Справочник,
Маркировка резисторов,
Отключить защиту инвертора,
Замена BU808DFI,
Замена SMR40200,
Колебательный контур и резонансная частота,
Постоянная времени RC,
Реактивное сопротивление L C,
Реактивная мощность. Расчёт,
ESR конденсатора. Теория,
Измерение ESR конденсатора.
Замечания и предложения принимаются и приветствуются!
Расчет цепей переменного тока | Онлайн журнал электрика
Хоть какой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают таковой ток, закон конфигурации которого во времени есть синусоидальная функция.
Математическое выражение для синусоидального тока можно записать в виде:
где, i — секундное значение тока, показывающее величину тока в определенный момент времени, Im — амплитудное (наибольшее) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f — частота переменного тока, это величина, оборотная периоду конфигурации синусоидальной величины Т, ω — угловая частота, ω = 2πf = 2π / T, α — исходная фаза, указывает значение фазы в момент времени t = 0.
Аналогичное выражение можно записать и для синусоидального переменного напряжения:
Секундные значения тока и напряжения договорились обозначать строчными латинскими знаками i, u, а наибольшие (амплитудные) значения – строчными печатными латинскими знаками I, U с индексом m.
Для измерения величины переменного тока в большинстве случаев употребляют действующее (действенное) значение, которое численно равно такому неизменному току, который за период переменного выделяет в нагрузке такое же количество тепла, что и переменный ток.
Действующее значение переменного тока:
Для обозначения действующих значений тока и напряжения употребляют строчные печатные латинские буковкы I, U без индекса.
В цепях синусоидального тока меж амплитудным и действующим значениями существует связь:
В цепях переменного тока изменение во времени питающего напряжения влечёт за собой изменение тока, также магнитного и электронного полей, связанных с цепью. Результатом этих конфигураций является появление ЭДС самоиндукции и взаимоиндукции в цепях с катушками индуктивности, а в цепях с конденсаторами возникают зарядные и разрядные токи, которые делают сдвиг по фазе меж напряжениями и токами в таких цепях.
Отмеченные физические процессы учитывают введением реактивных сопротивлений, в каких, в отличие от активных, не происходит перевоплощение электронной энергии в другие виды энергии. Наличие тока в реактивном элементе разъясняется повторяющимся обменом энергией меж таким элементом и сетью. Все это усложняет расчёт цепей переменного тока, потому что приходится определять не только лишь величину тока, да и его угол сдвига по отношению к напряжению.
Все главные законы цепей неизменного тока справедливы и для цепей переменного тока, но только для моментальных значений либо значений в векторной (всеохватывающей) форме. На базе этих законов можно составить уравнения, дозволяющие выполнить расчёт цепи.
Обычно, целью расчёта цепи переменного тока является определение токов, напряжений, углов сдвига фаз и мощностей на отдельных участках. При составлении уравнений для расчёта таких цепей выбирают условные положительные направления ЭДС, напряжений и токов. Получаемые уравнения для моментальных значений в установившемся режиме и синусоидальном входном напряжении будут содержать синусоидальные функции времени.
Аналитический расчёт тригонометрических уравнений неудобен, просит значимых издержек времени и потому не находит широкого распространения в электротехнике. Упростить анализ цепи переменного тока можно, используя тот факт, что синусоидальную функцию можно условно изобразить вектором, а вектор, в свою очередь, можно записать в виде всеохватывающего числа.
Всеохватывающим числом именуют выражение вида:
где a – вещественная (действительная) часть всеохватывающего числа, j – надуманная единица, b – надуманная часть, A – модуль, α– аргумент, e – основание натурального логарифма.
1-ое выражение представляет собой алгебраическую форму записи всеохватывающего числа, 2-ое – показательную, а третье – тригонометрическую. Для отличия, в всеохватывающей форме записи подчеркивают буковку, обозначающую электронный параметр.
Способ расчёта цепи, основанный на применении всеохватывающих чисел, именуется символическим способом. В символическом способе расчета все реальные характеристики электронной цепи подменяют знаками в всеохватывающей форме записи. После подмены реальных характеристик цепи на их всеохватывающие знаки расчет цепей переменного тока делают способами, которые применяли для расчета цепей неизменного тока. Отличие заключается в том, что все математические операции нужно делать с всеохватывающими числами.
В итоге расчета электронной цепи разыскиваемые токи и напряжения получаются в виде всеохватывающих чисел. Реальные действующие значения тока либо напряжения равны модулю соответственного комплекса, а аргумент всеохватывающего числа указывает угол поворота вектора на всеохватывающей плоскости по отношению к положительному направлению вещественной оси. При положительном аргументе вектор поворачивается против часовой стрелки, а в случае отрицательного аргумента – по часовой.
Завершают расчёт цепи переменного тока, обычно, составлением баланса активных и реактивных мощностей, который позволяет проверить корректность вычислений.
Школа для электрика
Расчет электрических цепей постоянного тока, не содержащих источников ЭДС
Расчет электрических цепей
постоянного тока, не содержащих
источников ЭДС
1.Последовательное соединение резисторов
Резистор – элемент цепи с заметным сопротивлением
R
I
R1
U1
R2
R3
U2
U3
U
I
Rобщ
I const
U U1 U 2 U 3 …
IR IR1 IR2 IR3 …
Rобщ R1 R2 R3 …
U
2. Параллельное соединение резисторов
I1
R1
I2
R2
I3
R3
I
U const
I I1 I 2 I 3 …
U
U U U
…
Rобщ R1 R2 R3
U
I
Rобщ
U
1
Rобщ
1
1
1
…
R1 R2 R3
3. Смешанное соединение резисторов
А) Метод последовательного упрощения цепи
R
A
B
R
R
R1
3R
R
R
R
A
B
R
3R
2.75R
4
3R
R
R 3R 3R
R 3R
4
R AB R R
R1
R
RAB
R
A
B
R
3R
4
Б) Метод поиска точек с одинаковыми потенциалами
Если две точки цепи имеют одинаковые потенциалы, то
1) Их можно соединять
2) Их можно разъединять
3) Резисторы, включенные между ними, можно исключить
Как узнать, что потенциалы точек одинаковы?
Точки имеют одинаковые потенциалы, если:
1) Они соединены проводником с нулевым сопротивлением
2) Они симметричны геометрически и по отношению к
точкам подключения
Задача
Определить сопротивление проволочного куба при подключении к двум
наиболее удаленным друг от друга вершинам. Сопротивление каждого ребра
куба равно R
B
F
C
A B
C D E
F G H
G
D
A
H
E
A
C
D
R E
3
R
6
F
G
H R
3
B
В) Общий метод расчета общего сопротивления
R2
R1 C
A
B
R5
R3
RAB — ?
R4
R1 R3
R2 R4
C D
R1 R3
R2 R4
C D
D
I
I
U
Приложим к концам цепи напряжение U
и рассчитаем ток I, протекающий через
цепь
По закону Ома
R
U
I
I1
A
R1 C
I5
I2
Найти: I, I1, I2, I3, I4, I5
B
R5
R3
I3
R2
Дано: U, R1, R2, R3, R4, R5
Необходима система из 6 неза-висимых
уравнений для токов
R4
D
I4
I
I
U
Закон сохранения заряда:
A : I I1 I 3
(1)
B : I I2 I4
C : I1 I 2 I 5
D : I3 I5 I 4
(2)
(3)
I1
A
R1 C R2 I 2
R5
R4
R3
I 3 D I 4
I5
Работа сил электрического поля над
зарядом не зависит от траектории
движения заряда
B
I
I
U
Работа сил электрического поля над
зарядом при премещении по замкнутому
контуру равна нулю
ADCB : I 3 R3 I 5 R5 I 2 R2 U (4)
ACBDA : I1R1 I 2 R2 I 4 R4 I3R3 0 (5)
Записанные уравнения объединим в систему:
I I1 I3 0
I I2 I4 0
I1 I 2 I5 0
I1R1 I5 R5 I 2 R2 U
I1R1 I 2 R2 I 4 R4 I3R3 0
Общее решение системы имеет вид
I U f ( R1, R2 , R3 , R4 , R5 )
По определению
R
U
I
1
f ( R1, R2 , R3 , R4 , R5 )
Расчет разветвлённых электрических
цепей постоянного тока, содержащих
источники ЭДС
1. Метод Кирхгофа
Сложная электрическая цепь постоянного тока содержит произвольным
образом соединенные источники тока и резисторы.
Задача расчета сложной цепи состоит в определении всех неизвестных
токов, текущих в цепи.
В методе Кирхгофа расчёт начинается с расстановки токов, текущих в
ветвях схемы. Направление тока в каждой ветви выбирается произвольно.
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
4
B
C
Общее число уравнений, составленных для расчёта цепи, равно числу
неизвестных токов.
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
В данной цепи для расчета токов I1, I2, I3, I4, I5 необходимо составить 5
независимых уравнений
Для составления уравнений используются 2 правила Кирхгофа
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
Первое правило Кирхгофа формулируется для узлов цепи. Узел — точка
цепи, в которой сходится не менее 3-х проводников.
Ветвь схемы – участок электрической цепи между соседними узлами.
Первое правило Кирхгофа:
В любом узле цепи сумма входящих токов равна сумме выходящих
токов.
2
1
R1
R2
A
I2
I4
I1
3
R4
R3
I3
R5
I5
C
4
B
Для узла А
I1 I 2 I3 I 4
или
I1 I 2 I3 I 4 0 (1)
Для узла В
I 4 I1 I5
или
I1 I 4 I5 0 (2)
Число независимых уравнений, составленных по первому правилу Кирхгофа,
на одно уравнение меньше числа узлов в цепи
Второе правило Кирхгофа формулируется для контуров, которые
можно выделить в рассматриваемой схеме. Контур – любая замкнутая
часть схемы.
2
1
3
R1
R2
A
I2
I4
I1
R4
R3
I3
R5
I5
C
4
B
Работа сил электрического поля при перемещении заряда по произвольному замкнутому контуру равна нулю. Запишем это равенство для
наружного контура рассматриваемой цепи:
R1
1
2
3
R2
I1
q
R5
I5
ЭП
ЭП
ЭП
ЭП
ЭП
ARЭП
A
A
A
A
A
1
2
R2
3
R5 0
1
qI1R1 q 1 q 2 qI 2 R2 q 3 qI 5 R5 0
I1R1 I 2 R2 I5 R5 1 2 3
I2
Второе правило Кирхгофа:
Для любого замкнутого контура цепи, при выбранном направлении обхода
контура, алгебраическая сумма напряжений на резисторах контура равна
алгебраической сумме ЭДС источников тока, встреченных при обходе
контура. Направление обхода контура выбирается произвольно.
В сумму напряжений на резисторах слагаемые входят со знаком «+», если
направление тока текущего через резистор, совпадает с направлением
обхода, и со знаком «-», если направления противоположны.
В сумму ЭДС слагаемые входят со знаком «+», если направление ЭДС,
Источника совпадает с направлением обхода, и со знаком «-», если
направления противоположны
Число независимых
уравнений, которые можно
составить по второму правилу
Кирхгофа равно числу
простых контуров цепи
1
R1
1
R4
2
3
R2
R3
4
R5
2
3
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
BR1R2CB :
I1R1 I 2 R2 I5 R5 1 2 3
(3)
BAR2CB :
I 4 R4 I 2 R2 I5 R5 4 2 3
(4)
AR3CR2 A :
I3R3 I 2 R2 3 2
(5)
I1 I 2 I3 I 4 0
(1)
I1 I 4 I5 0
(2)
I1R1 I 2 R2 I5 R5 1 2 3
(3)
I 4 R4 I 2 R2 I5 R5 4 2 3 (4)
I3R3 I 2 R2 3 2
(5)
Для любой сколь угодно сложной цепи правила Кирхгофа позволяют
составить достаточное число независимых уравнений для нахождения всех
токов в цепи
3. Метод контурных токов
Недостаток метода Кирхгофа — в необходимости решения системы
уравнений, число которых равно числу неизвестных токов. Достаточно
простая схема, содержащая много ветвей, приводит к системе из большого
числа уравнений, что усложняет вычисления.
В методе контурных токов число уравнений сводится к числу простых
контуров, содержащихся в рассматриваемой схеме.
В качестве примера, применим метод контурных токов
для расчёта цепи, рассмотренной в методе Кирхгофа.
Полагаем, что в каждом
простом контуре течёт свой
«контурный ток». Направление «контурных токов» во
всех контурах одинаково: по
часовой или против часовой
стрелки.
1
R1
i1
1
R4
4
2
R2
R3
i3
R5
3
i2
2
3
Для нахождения «контурных токов», для каждого контура составляется
уравнение по второму правилу Кирхгофа.
Для конура №1:
Для контура №2
Для контура №3
R1i1 (i1 i3 ) R4 1 4
(1)
R2i2 (i2 i3 ) R3 2 3
(2)
R5i3 R4 (i3 i1 ) R3 (i3 i2 ) 4
(3)
Раскрывая скобки и приводя подобные получим систему уравнений для
нахождения «контурных токов»:
R1 R4 i1 R4i3 1 4
R2 R3 i2 R3i3 2 3
R4i1 R3i2 R3 R4 R5 i3 4
После решения системы возвращаемся к исходной схеме, и находим
неизвестные токи, текущие в ветвях схемы:
I1 i1; I 2 i2 ; I 3 i3 i2 ;
I 4 i3 i1;
I 5 i3
Полученное с отрицательным знаком значение тока свидетельствует о
противоположном предполагаемому направлении тока в данной ветви.
Сокращение числа уравнений на два, по сравнению с методом Кирхгофа,
делает применение метода контурных токов более предпочтительным.
Калькулятор RC-цепи
Используйте этот калькулятор RC-цепи для вычисления характеристической частоты RC-цепи. Вы также можете использовать его как калькулятор времени заряда конденсатора (калькулятор постоянной времени RC) или как калькулятор RC-фильтра. В зависимости от потребности RC-цепь может служить фильтром нижних или верхних частот.
RC цепь
RC-цепь представляет собой базовую электрическую цепь, в которой резистор сопротивлением R последовательно соединен с конденсатором емкостью C .Такая схема характеризуется частотой f и имеет два основных применения:
- RC-цепь может использоваться как фильтр,
- и конденсатор можно использовать для хранения энергии.
Вы можете использовать наш калькулятор RC цепей как
- Калькулятор RC-фильтров,
- калькулятор времени заряда конденсатора.
Если вы хотите узнать больше о сопротивлении и емкости, воспользуйтесь нашим калькулятором конденсаторов с параллельными пластинами.
Калькулятор RC-фильтров
Характеристическая частота f определяет частоту сигналов, которые могут проходить по цепи. RC-цепь подавляет частоты меньше f , и сигналы с частотами больше f могут течь свободно. Однако это не совсем четкая ситуация, и сигналы с частотами около f все еще передаются частично. В зависимости от конфигурации вы можете использовать RC-фильтр для фильтрации низких или высоких частот.Это фильтры высоких и низких частот.
Если вы объедините фильтр низких частот с фильтром высоких частот, вы получите широкополосный фильтр, который подавляет все сигналы ниже и выше некоторых частот. Все наше музыкальное оборудование оснащено широкополосными фильтрами.
Калькулятор времени заряда конденсатора
Если мы подключим RC-цепь к источнику постоянного тока, конденсатор начнет накапливать электрический заряд, пока не станет полностью заряженным. Это время зависит от емкости конденсатора C и сопротивления резистора R , регулирующего ток, который представляет собой количество заряда, попадающего в конденсатор за одну секунду.Чем больше емкость или сопротивление, тем дольше заряжается конденсатор. Зарядка конденсатора — экспоненциальный процесс: чем больше заряда, тем больше времени требуется для его накопления. Время заряда конденсатора — это время, за которое конденсатор заряжается примерно до 63%. Если вы удвоите время, вы получите около 87%. Чтобы проверить калькулятор времени заряда конденсатора, щелкните Расширенный режим.
Калькулятор постоянной времени RC
Уравнение для характеристической частоты f RC-цепи равно
f = 1 / (2π * R * C)
где
-
R— сопротивление резистора (в Ом), -
C— емкость конденсатора (в Фарадах), -
f— характеристическая частота (в Герцах)
Чтобы вычислить частоту, просто укажите сопротивление и емкость в калькуляторе.Вы также можете зафиксировать частоту и, например, сопротивление, чтобы найти необходимую емкость.
Время заряда конденсатора т равно
t = R * C
Чтобы проверить время заряда конденсатора, откройте расширенный режим.
Вы также можете попробовать другие калькуляторы, связанные с электрическими цепями, например, калькулятор коэффициента мощности.
Калькулятор цепи резистор-конденсатор (RC) • Калькуляторы электрических, радиочастотных и электронных устройств • Онлайн-конвертеры единиц
Постоянная времени определяется как
, где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах.Постоянная времени RC-цепи определяется как время, за которое конденсатор достигает 63,2% своей максимальной зарядной емкости при отсутствии начального заряда. Обратите внимание, что конденсатор будет заряжен на 63,2% после τ и почти полностью заряжен (99,3%) примерно через 5 τ .
Накопленная энергия E в конденсаторе, когда он полностью заряжен до напряжения U (время зарядки T >> τ )
, где C — емкость в фарадах, а V — напряжение в вольтах.
Максимальный ток I определяется по закону Ома:
Максимальный заряд Q определяется следующим образом:
, где C — емкость в фарадах, а U — напряжение в вольтах.
Фильтр электролитических конденсаторов на материнской плате компьютера
Приложения
Основная часть разветвителя ADSL — это фильтр нижних частот.
Конденсаторы часто используются в различных электронных и электрических устройствах и системах.Вы, вероятно, не найдете электронное устройство без хотя бы одного конденсатора. Конденсаторы используются для накопления энергии, обеспечения импульсной мощности, для согласования мощности, для коррекции коэффициента мощности, для связи по переменному току и блокировки постоянного тока, в электронных частотных фильтрах, в шумовых фильтрах, для запуска двигателя, для хранения информации, в настроенных схемах, в различных сенсорные устройства, емкостные сенсорные экраны мобильных телефонов и для многих других целей.
Резисторно-конденсаторные (RC) схемы можно использовать в качестве простых фильтров нижних и верхних частот, интеграторов и дифференциаторов.
RC-фильтры нижних частот
Пример двухкаскадного RC-фильтра нижних частот второго порядка с неинвертирующим единичным усилителем, который используется в качестве буфера между двумя каскадами фильтра.
Фильтры нижних частот пропускают только низкочастотные сигналы и ослабляют высокочастотные сигналы. Частота среза определяется компонентами схемы фильтра.
Такие фильтры широко используются в электронике. Один из примеров — их использование в сабвуферах для блокировки высоких частот, которые они не могут воспроизвести.Они также используются в радиопередатчиках для блокировки нежелательных гармонических излучений. Те, кто использует подключение к Интернету ADSL, устанавливают эти фильтры в разветвители DSL, которые предотвращают помехи между телефонами и оборудованием DSL, подключенным к телефонной линии.
Фильтры нижних частот используются для согласования сигналов перед аналого-цифровым преобразованием и называются фильтрами сглаживания. Они необходимы для подавления высокочастотных составляющих сигнала выше частоты Найквиста, чтобы удовлетворить теорему дискретизации.
Простой фильтр нижних частот показан на рисунке выше. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот. Более сложные пассивные фильтры нижних частот также используют индукторы.
В отличие от пассивных фильтров нижних частот, в активных фильтрах используются некоторые устройства усиления, например, транзисторы или операционные усилители. Пассивные фильтры также часто сопровождаются усилителями. В зависимости от количества конденсаторов и катушек индуктивности, которые влияют на крутизну частотной характеристики фильтра, их часто называют «первого порядка», «второго порядка» и т. Д.фильтры. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.
Простой пассивный RC-фильтр верхних частот первого порядка
RC-фильтр верхних частот
Фильтры верхних частот пропускают только высокочастотные сигналы и ослабляют низкочастотные сигналы. Фильтры верхних частот используются, например, в кроссоверах аудио для блокировки низких частот сигналов, посылаемых на твитеры, которые обычно не способны обрабатывать сигналы большой мощности на низких частотах.
Активный фильтр верхних частот с операционным усилителем
Фильтры верхних частот часто используются для блокировки постоянного тока от схем, чувствительных к нему.Например, они очень распространены в схемах микрофонов, потому что микрофонам требуется питание постоянного тока, которое подается через микрофонный кабель. В то же время они записывают только сигналы переменного тока, такие как человеческий голос и музыку. Напряжение постоянного тока не должно появляться на выходе микрофона, и для его блокировки используется фильтр высоких частот.
Простой полосовой фильтр, состоящий из каскадного соединения фильтра нижних частот (C2, R2) и фильтра верхних частот (C1, R1)
Если фильтры верхних частот и нижних частот используются вместе, они образуют полосовой фильтр , который пропускает частоты только в определенном диапазоне и ослабляет частоты за пределами этого диапазона.Такие фильтры широко используются в беспроводных приемниках и передатчиках. В приемниках полосовые фильтры пропускают и слышат только сигналы в выбранном диапазоне частот, подавляя сигналы на нежелательных частотах. Передатчики всегда должны передавать мощность только в выделенном им диапазоне частот; поэтому в них используются полосовые фильтры, чтобы ограничить полосу пропускания выходного сигнала их полосой передачи.
Импеданс R, C и L параллельно Калькулятор
- Цель использования
- помогает проверить мои ответы на мои задания
[1] 2021.01.22 10:59 Мужчина / 20-летний уровень / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- цель двойной проверки моих ответов и лучшего понимания импеданса
[2] 2020/12/08 06:02 — / Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Понимание работы в колледже
- Комментарий / запрос
- Очень полезно, так как я изучаю инженерное дело и изо всех сил пытаюсь учиться дома из-за текущих ограничений Covid-19.Если бы шаги были включены, это тоже было бы очень полезно.
[3] 2020/11/19 01:27 Мужчина / До 20 лет / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Двойная проверка ответов
- Комментарий / запрос
- Очень полезно в использовании.
[4] 2020.10.26 17:08 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Полезно /
- Цель использования
- проверка ответов на практические задачи
[5] 2020/10/23 12:22 Мужской / 50-летний уровень / Учитель / Исследователь / Полезный /
- Цель использования
- хобби
[6] 2020 / 07/26 01:54 Мужчина / Уровень 60 и старше / Инженер / Полезный /
- Цель использования
- соответствует
- Комментарий / Запрос
- спасибо
[7] 2019/12/23 15:53 Мужской / уровень 30 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Хобби
- Комментарий / Запрос
- Просто ищу полезность в будущем
[8] 2019/09/18 03:31 — / Уровень 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Проверить конструкцию фильтров.это очень полезно
[9] 30.10.2018 23:33 Мужской / 50-летний уровень / An инженер / Вери /
- Цель использования
- Домашнее задание.
- Комментарий / запрос
- Бог знает, как работают все эти формулы, но мне нужно было найти импеданс цепи с сопротивлением 18 Ом, индуктивностью 100 мГн и питанием 50 Гц. Жаль, что нет поля для питания, если это имеет значение? 110V я искал.
[10] 2017/09/21 01:04 Мужчина / 30-летний уровень / Средняя школа / Университет / Аспирант / Очень /
Добавьте параллельные резисторы в схему
Если комбинация резисторов обеспечивает несколько путей для прохождения тока, она называется параллельными резисторами.Эквивалентное сопротивление всегда уменьшается, когда мы добавляем параллельные резисторы. Воспользуйтесь онлайн-калькулятором параллельных резисторов здесь.
Параллельная комбинация:
Комбинация резисторов будет называться резисторами, включенными параллельно , если к одному узлу в цепи подключено более двух компонентов.
Предположим, у нас есть три резистора, подключенных друг к другу в точке b, головка первого резистора подключена к головке второго и третьего резистора.Предполагая, что ток течет сверху вниз. В отличие от последовательной комбинации, положительный вывод R 1 соединен с положительным выводом R 2 и R 3 . Комбинация приведет к трем различным путям для тока.
Обратите внимание, что в узле a и узле b присутствуют четыре компонента; источник, R 1 , R 2, и R 3 , как показано на диаграмме.
Параллельная цепь обеспечивает более одного пути для тока.
Онлайн-калькулятор параллельных резисторов:
Для расчета общего сопротивления резисторов, которые соединены параллельно, используйте следующий калькулятор параллельных резисторов. $ R_1, R_2 $ и $ R_3 $ — это три резистора, соединенных параллельно, а $ R_ {Total} $ — эквивалентное сопротивление.
Калькулятор тока параллельной цепи
После расчета общего сопротивления параллельных резисторов теперь вы можете рассчитать общий ток. Поместите общее сопротивление из онлайн-калькулятора параллельных резисторов, указанного выше.Также введите напряжение цепи, чтобы рассчитать ток.
Устранение резисторов в параллельной цепи:
Мы хотим знать несколько типов параметров для вышеупомянутой схемы, как мы это сделали для последовательной комбинации.
Общее эквивалентное сопротивление:
Каков общий ток, обеспечиваемый источником?
Чтобы ответить на вопрос, нам нужно вычислить полное или эквивалентное сопротивление цепи. И формула для этого:
$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $
Если мы используем те же номиналы резисторов, которые мы использовали в последовательной схеме i.е. R $ _ {1} $, R $ _ {2,} $ и R $ _ {3} $ равны 20, 40 и 10 $ \ Omega $ соответственно. И поместите эти значения в приведенную выше формулу, тогда:
$ \ frac {1} {R_ {Eq}} = \ frac {1} {20} + \ frac {1} {40} + \ frac {1} { 10} = \ frac {7} {40} $
$ R_ {Eq} = \ frac {40} {7} = 5.714 \ Omega $
Вышеупомянутая сложная схема теперь сведена к этой схеме с одним резистором. Теперь мы можем легко определить полный ток, потребляемый схемой, по закону Ома, как показано ниже:
$ I_ {T} = \ frac {V} {R_ {Eq}} = \ frac {140 v} {5.714 \ Omega } $
$ I_ {T} = 24.5 A $
Общее сопротивление намного меньше, чем у последовательной цепи, а общий ток намного больше, чем у последовательной цепи.
Напряжение на каждом резисторе:
Какое напряжение на каждом резисторе?
Прежде всего, взгляните на схему, и вы поймете, что каждый резистор подключен к источнику напряжения. Напряжение на каждом резисторе такое же, как напряжение источника. Формула для напряжения:
$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $
В нашем случае напряжение для R $ _ {1} $, R $ _ {2} $ и R $ _ {3} $: V $ _ {1} $ = 140 v, V $ _ {2} $ = 140 v и V $ _ {3} $ = 140 v соответственно.
Ток каждого резистора:
Какой ток каждого резистора?
Мы можем использовать закон Ома для определения тока. Предположим, что ток для R $ _ {1} $, R $ _ {2,} $ и R $ _ {3} $ равен I $ _ {1} $, I $ _ {2,} $ и I $ _ {3} $ соответственно. Итак, применив закон Ома к каждому резистору, мы получим
$ I_ {1} = \ frac {V_ {1}} {R_ {1}} = \ frac {140 v} {20 \ Omega} = 7 A $
$ I_ {2} = \ frac {V_ {2}} {R_ {2}} = \ frac {140 v} {40 \ Omega} = 3,5 A $
$ I_ {3} = \ frac {V_ {3} } {R_ {3}} = \ frac {140 v} {10 \ Omega} = 14 A $
А что, если мы сложим все эти отдельные токи? Давай сделаем это.
$ I_ {T} = I_ {1} + I_ {2} + I_ {3} $
$ I_ {T} = 7 A + 3,5 A + 14 A $
$ I_ {T} = 24,5 A $
Такой же ток может быть подтвержден с помощью вычислителя параллельных резисторов выше.
Наконец-то! Мы получили полный ток, потребляемый всеми этими резисторами, так как мы нашли первое место. Это означает, что полный ток цепи равен сумме токов отдельных резисторов. Мы можем обобщить формулу следующим образом:
$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $
Индивидуальный ток каждого резистора можно найти с помощью правила делителя тока. (CDR).
Формула для добавления параллельных резисторов:
В приведенном выше обсуждении мы наблюдали три параметра: первое общее сопротивление параллельно, второе, индивидуальное напряжение каждого резистора и, наконец, индивидуальный ток каждого резистора. Все эти формулы представлены здесь для вашей простоты с общей применимостью до n резисторов.
Полное сопротивление параллельной цепи:
$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $
Индивидуальное напряжение резисторов такое же, как и напряжение источника:
$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $
Суммарный ток складывается из всех индивидуальных токов:
$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $
Добавить параллельные резисторы То же значение:
Предположим, что схема, в которой все резисторы имеют одинаковое значение и все они подключены параллельно, каково будет общее сопротивление?
Предположим, что $ n $ количество параллельно подключенных резисторов с одинаковым сопротивлением.Общее сопротивление схемы будет
$ R_ {Total} = \ frac {R} {n} $
$ R $ — это значение сопротивления, которое одинаково для всех резисторов, а $ n $ равно количество резисторов, включенных параллельно.
Какой будет ток в каждом резисторе?
Ток каждого резистора будет
$ I = \ frac {I_ {Total}} {n} $
Вывод:
- Деление тока в параллельной цепи
- Добавьте параллельные резисторы, чтобы увеличить пути для тока
- Общий ток равен индивидуальному току параллельных цепей
- Напряжение остается неизменным в параллельных цепях электрической цепи
- Общее сопротивление уменьшается в параллельной цепи по сравнению с сопротивлением отдельных параллельных цепей
Мастер цепей — синий Морские системы
Мы думаем, что этот инструмент будет полезен персоналу любого уровня подготовки для быстрого выполнения расчетов и исключения многих неподходящих вариантов.Окончательное решение о защите проводов и цепей должно быть принято после обзора, основанного на дополнительных источниках, таких как стандарты ABYC или одной из многих книг в этой области.
ПРЕДУПРЕЖДЕНИЕ:
Все судовые электрические системы представляют собой риск возгорания и других опасностей. Blue Sea Systems не делает никаких заявлений и не гарантирует, что этот калькулятор будет подходить для решения вашей конкретной ситуации или требований.
Blue Sea Systems разработала этот калькулятор для использования только лицами, имеющими соответствующие практические знания и понимание морских электрических систем.Этот калькулятор частично основан на таблицах и стандартах ABYC, содержащихся в E-11 «Электрические системы переменного и постоянного тока на лодках», но он не предназначен для замены расчетов, основанных непосредственно на тех или иных отраслевых стандартах, которые могут применяться. Этот инструмент является прототипом и может содержать ошибки ввода или расчета.
Этот калькулятор не учитывает все возможные переменные и факторы, относящиеся к выбору сечения провода и защиты цепи. Такие переменные могут включать в себя перегрузки (например, изменение размера лампочек или добавление дополнительных нагрузок в цепи), ошибки проводки (например, слабые соединения или плохие обжимы), нагретые выводы (например, клеммы двигателя, нагревательные приборы или осветительные приборы), ошибки ввода данных, необычные источники тепла из окружающей среды, а также несоответствующая или неисправная изоляция проводов, дефекты программного обеспечения и / или сбои в работе браузера или серверного компьютера.
Этот калькулятор не заменяет профессиональные знания морского электрика. Ни при каких обстоятельствах этот калькулятор не должен использоваться в качестве единственной основы для выбора размера провода или защиты цепи. Любой размер провода или защита цепи, предварительно выбранные с помощью этого инструмента, должны быть проверены на адекватность перед установкой специалистом, применяющим применимые отраслевые стандарты.
Blue Sea Systems категорически отказывается от ответственности за любое использование этого калькулятора, которое приведет к ненадлежащему сечению проводов или защите цепи.
Веб-сайт класса физики
Электрические схемы: обзор набора проблем
Этот набор из 34 задач нацелен на вашу способность определять такие параметры цепи, как ток, сопротивление, разность электрических потенциалов, мощность и электрическая энергия, на основе словесных описаний и диаграмм физических ситуаций, относящихся к электрическим цепям.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синим цветом, .
Текущий
Когда заряд проходит по проводам электрической цепи , считается, что в проводах присутствует ток. Электрический ток — это измеримое понятие, которое определяется как скорость , с которой заряд проходит через точку в цепи.Его можно определить, измерив количество заряда, протекающего по площади поперечного сечения провода в цепи. Как величина скорости, ток (I) выражается следующим уравнением
I = Q / т
где Q — количество заряда, протекающего через точку за период времени t. Стандартной метрической единицей измерения величины тока является ампер, часто сокращенно Ампер или А. Ток в 1 ампер эквивалентен 1 кулону заряда, протекающему через точку за 1 секунду.Поскольку количество заряда, проходящего через точку в цепи, связано с количеством мобильных носителей заряда (электронов), которые проходят через эту точку, ток также может быть связан с количеством электронов и временем. Чтобы установить связь между током и числом электронов, нужно знать количество заряда на одном электроне.
Q электрон = 1,6 x 10 -19 C
Сопротивление
Когда заряд течет по цепи, он встречает сопротивление или препятствие для его прохождения.Как и ток, сопротивление — это измеримый термин. Величина сопротивления, обеспечиваемого сечением провода, зависит от трех переменных — материала, из которого сделан провод, длины провода и площади поперечного сечения провода. Одним из физических свойств материала является его удельное сопротивление — мера тенденции этого материала сопротивляться прохождению заряда через него. Значения удельного сопротивления для различных проводящих материалов обычно указаны в учебниках и справочниках. Зная значение удельного сопротивления (ρ) материала, из которого состоит провод, а также его длину (L) и площадь поперечного сечения (A), его сопротивление (R) можно определить с помощью приведенного ниже уравнения.
R = ρ • L / A
Стандартная метрическая единица измерения сопротивления — Ом (сокращенно греческой буквой Ом ).
Основная трудность при использовании приведенного выше уравнения связана с единицами выражения различных величин. Удельное сопротивление (ρ) обычно выражается в Ом • м. Таким образом, длина должна быть выражена в метрах, а площадь поперечного сечения — в метрах 2 . Многие провода круглые и имеют круглое сечение.Таким образом, площадь поперечного сечения в приведенном выше уравнении можно рассчитать, зная радиус или диаметр провода, используя формулу для площади круга.
A = π • R 2 = π • D 2 /4
Соотношение напряжение-ток-сопротивление
Величина тока, протекающего в цепи, зависит от двух переменных. Ток обратно пропорционален общему сопротивлению (R) цепи и прямо пропорционален разности электрических потенциалов, приложенной к цепи.Разность электрических потенциалов (ΔV), приложенная к цепи, — это просто напряжение, подаваемое источником энергии (батареи, розетки и т. Д.). Для домов в США это значение близко к 110–120 вольт. Математическая взаимосвязь между током (I), напряжением и сопротивлением выражается следующим уравнением (которое иногда называют уравнением закона Ома ).
Мощность
Электрические схемы — это энергия.Энергия включается в цепь аккумулятором или коммерческим поставщиком электроэнергии. Элементы схемы (освещение, обогреватели, двигатели, холодильники и даже провода) преобразуют эту электрическую потенциальную энергию в другие формы энергии, такие как световая энергия, звуковая энергия, тепловая энергия и механическая энергия. Мощность означает скорость, с которой энергия передается или преобразуется устройством или цепью. Это скорость, с которой энергия теряется или приобретается в любом заданном месте в цепи.Таким образом, общее уравнение мощности —
.
P = ΔE / т
Потеря (или усиление) энергии — это просто произведение разности электрических потенциалов между двумя точками и количества заряда, который перемещается между этими двумя точками за период времени t. Таким образом, потеря (или усиление) энергии равна просто ΔV • Q. Когда это выражение подставляется в вышеприведенное уравнение, уравнение мощности становится
P = ΔV • Q / т
Поскольку отношение Q / t, найденное в приведенном выше уравнении, равно току (I), приведенное выше уравнение также можно записать как
P = ΔV • I
Комбинируя уравнение закона Ома с приведенным выше уравнением, можно получить два других уравнения мощности.Их
| P = I 2 • R | P = ΔV 2 / R |
Стандартная метрическая единица измерения мощности — Вт . В единицах измерения ватт эквивалентен усилителю • Вольт, усилителю 2 • Ом и вольт 2 / Ом.
Затраты на электроэнергию
Коммерческая энергетическая компания взимает с домохозяйств ежемесячную плату за поставленную электроэнергию.В счете за услуги обычно указывается количество энергии, потребленной в течение месяца, в единицах по киловатт • час . Эта единица — единица мощности, умноженная на единицу времени, — это единица энергии. Домохозяйство обычно оплачивает счет на основе количества кВт • ч электроэнергии, потребленной в течение месяца. Таким образом, задача определения стоимости использования конкретного прибора в течение заданного периода времени довольно проста. Сначала необходимо определить мощность и преобразовать ее в киловатты.Затем эту мощность необходимо умножить на время использования в часах, чтобы получить потребляемую энергию в единицах кВт • час. Наконец, это количество энергии должно быть умножено на стоимость электроэнергии в соотношении $ / кВт • час, чтобы определить стоимость в долларах.
Эквивалентное сопротивление
Довольно часто в цепи используется более одного резистора. Хотя каждый резистор имеет собственное индивидуальное значение сопротивления, общее сопротивление цепи отличается от сопротивления отдельных резисторов, составляющих цепь.Величина, известная как эквивалентное сопротивление , указывает полное сопротивление цепи. Концептуально эквивалентное сопротивление — это сопротивление, которое один резистор будет иметь, чтобы оказывать такое же общее влияние на сопротивление, как и комбинация резисторов, которые присутствуют. Таким образом, если в цепи есть три резистора с эквивалентным сопротивлением 25 Ом, то один резистор на 25 Ом может заменить три отдельных резистора и оказать влияние на схему, эквивалентное .Значение эквивалентного сопротивления (R eq ) учитывает индивидуальные значения сопротивления резисторов и способ их подключения.
Есть два основных способа включения резисторов в электрическую цепь. Они могут быть соединены последовательно или параллельно . Резисторы, которые соединены последовательно, подключаются последовательно, так что весь заряд, который проходит через первый резистор, также проходит через другие резисторы.При последовательном соединении весь заряд, протекающий по цепи, проходит через все отдельные резисторы. Таким образом, эквивалентное сопротивление последовательно соединенных резисторов является суммой значений отдельных сопротивлений этих резисторов.
R eq = R 1 + R 2 + R 3 +… (последовательные соединения)
Параллельно подключенные резисторы подключаются бок о бок, так что заряд, приближающийся к резисторам, разделяется на два или более разных пути.Параллельно подключенные резисторы характеризуются наличием участков разветвления, в которых заряд разветвляется по разным путям. Заряд, который проходит через один резистор, не проходит через другие резисторы. Эквивалентное сопротивление параллельно включенных резисторов меньше значений сопротивлений всех отдельных резисторов в цепи. Хотя это может быть не совсем интуитивно понятным, уравнение эквивалентного сопротивления параллельно соединенных резисторов дается уравнением с несколькими взаимными членами.
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 +… (параллельное соединение)
Анализ последовательной цепи
Некоторые проблемы второй половины этого набора относятся к последовательным цепям. Нередко проблема сопровождается чертежом или схемой, показывающей расположение батарей и резисторов. Чертеж и соответствующая принципиальная схема ниже представляют последовательную цепь, питаемую тремя ячейками и имеющую три последовательно соединенных резистора (лампочки).
Если представить себе заряд, покидающий положительный полюс батареи и следующий по своему пути, когда он пересекает полный контур, становится очевидным, что заряд проходит через все резисторы последовательно. Таким образом, он соответствует критериям последовательной цепи. Знание того, что схема является последовательной, позволяет связать общее или эквивалентное сопротивление цепи с отдельными значениями сопротивления с помощью уравнения эквивалентного сопротивления, описанного выше.
R eq = R 1 + R 2 + R 3 +… (последовательные соединения)
Ток последовательной цепи в резисторах такой же, как и в батарее. Поскольку нет ответвлений в местах, где заряд разделяется на пути, можно сказать, что ток в батарее равен току в резисторе 1, равен току в резисторе 2 и равен току в резисторе 3 .. ., В форме уравнения можно записать, что
I аккумулятор = I 1 = I 2 = I 3 =… (последовательные цепи)
Когда заряд проходит через резисторы последовательной цепи, происходит падение электрического потенциала, когда он проходит через каждый резистор.Это падение электрического потенциала на каждом резисторе определяется током через резистор и сопротивлением резистора. Это согласуется с уравнением закона Ома, описанным выше (ΔV = I • R). Поскольку ток (I) в каждом отдельном резисторе одинаков, логично заключить, что резисторы с наибольшим сопротивлением (R) будут иметь наибольшую разность электрических потенциалов (ΔV), приложенную к ним.
Разность электрических потенциалов на отдельных резисторах цепи часто обозначается как , падение напряжения .Эти падения напряжения последовательно соединенных резисторов математически связаны с электрическим потенциалом или номинальным напряжением элементов или батареи, которые питают цепь. Если заряд приобретает 12 В электрического потенциала при прохождении через батарею электрической цепи, то он теряет 12 В при прохождении через внешнюю цепь. Это падение электрического потенциала на 12 В является результатом серии отдельных падений электрического потенциала, когда он проходит через отдельные резисторы последовательной цепи.Эти отдельные падения напряжения (разность электрических потенциалов) в сумме дают общее падение напряжения в цепи. В форме уравнения можно сказать, что
ΔV аккумулятор = ΔV 1 + ΔV 2 + ΔV 3 +… (последовательные цепи)
где ΔV аккумулятор — электрический потенциал, накопленный в аккумуляторе, а ΔV 1 , ΔV 2 и ΔV 3 — это падения напряжения (или разности электрических потенциалов) на отдельных резисторах.
Более подробное и исчерпывающее обсуждение последовательных схем и их анализа можно найти в учебном пособии по физике.
Анализ параллельных цепей
Самые последние проблемы в этом наборе относятся к параллельным цепям. Опять же, нет ничего необычного в том, что проблема сопровождается чертежом или схематической диаграммой, показывающей расположение батарей и резисторов.Чертеж и соответствующая принципиальная схема ниже представляют собой параллельную цепь с питанием от трех ячеек и имеющую три параллельно соединенных резистора (лампочки).
Если представить заряд, покидающий положительный полюс батареи и следующий по своему пути, когда он проходит через полный контур, становится очевидным, что заряд достигает места разветвления до достижения резистора. В месте разветвления, которое иногда называют узлом, заряд проходит по одному из трех возможных путей через резисторы.Вместо того, чтобы проходить через каждый резистор, один заряд будет проходить через единственный резистор во время полного цикла вокруг цепи. Таким образом, он соответствует критериям параллельной цепи. Знание того, что схема является параллельной, позволяет связать общее или эквивалентное сопротивление цепи с отдельными значениями сопротивления с помощью уравнения эквивалентного сопротивления, описанного выше.
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 +… (параллельное соединение)
В месте разветвления заряд разделяется на отдельные пути.Таким образом, ток в отдельных путях будет меньше, чем ток вне путей. Общий ток в цепи и ток в батарее равны сумме тока в отдельных проводящих путях. В форме уравнения можно записать, что
I аккумулятор = I 1 + I 2 + I 3 +… (параллельные цепи)
Текущие значения этих отдельных ветвей контролируются двумя величинами — сопротивлением резистора в ветви и разностью электрических потенциалов (ΔV), приложенной к ветви.В соответствии с уравнением закона Ома, рассмотренным выше, можно сказать, что ток в ветви 1 равен разности электрических потенциалов на ветви 1, деленной на сопротивление ветви 1. Аналогичные утверждения можно сделать и для других ветвей. В форме уравнения можно сказать, что
| I 1 = ΔV 1 / R 1 | I 2 = ΔV 2 / R 2 | I 3 = ΔV 3 / R 3 |
Эклектические разности потенциалов (ΔV 1 , ΔV 2 и ΔV 3 ) на отдельных резисторах часто называют падениями напряжения.Подобно последовательным цепям, любой заряд, покидающий батарею, должен испытывать такое же падение напряжения, как и усиление, которое он обнаруживает при прохождении через батарею. Но в отличие от последовательных цепей, в параллельной цепи заряд проходит только через один резистор. Таким образом, падение напряжения на этом резисторе должно равняться разности электрических потенциалов на батарее. В форме уравнения можно сказать, что
ΔV аккумулятор = ΔV 1 = ΔV 2 = ΔV 3 +… (параллельные цепи)
где ΔV аккумулятор — электрический потенциал, накопленный в аккумуляторе, а ΔV 1 , ΔV 2 и ΔV 3 — это падения напряжения (или разности электрических потенциалов) на отдельных резисторах.
Более подробное и исчерпывающее обсуждение параллельных схем и их анализа можно найти в Учебнике по физике.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки.Эти привычки кратко описаны здесь. Эффективное решение проблем …
- … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … идентифицирует известные и неизвестные величины и записывает их в организованном порядке, часто записывая их на самой диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например,г., ΔV = 9,0 В; R = 0,025 Ом; Я = ???).
- … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания принципов физики.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы Учебного пособия по физике могут быть полезны для того, чтобы помочь вам в понимании концепций и математики, связанных с этими проблемами.
Набор проблем электрических цепей
Просмотреть набор задач
Электрические схемы Решения с аудиогидом
Просмотрите аудиогид решения проблемы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34
Онлайн-калькулятор делителя тока
Apogeeweb
В электронике делитель тока представляет собой простую линейную схему, которая производит выходной ток, составляющий часть входного тока.Для расчета силы тока в любой из ветвей цепи формула:
Где
I n — ток через отдельную ветвь. Используя закон Ома ( I = E / R ), вы можете рассчитать ток каждой ветви.
I s — ток от источника тока.
R всего — эквивалентное параллельное сопротивление всех резисторов.
R n — сопротивление отдельной ветви.
Чтобы использовать этот калькулятор, все, что пользователи должны сделать, это ввести значение тока, поступающего из таблицы источника тока, и каждое из сопротивлений ветвей в цепи. Отношение полного сопротивления к индивидуальному сопротивлению такое же, как отношение индивидуального (ответвленного) тока к общему току.Вы можете проверить расчеты, так как в соответствии с Правилом Кирхгофа все токи ответвления будут равны полному току.
Люди тоже спрашивают (Q&A)
1. Какая формула для тока?
Ток обычно обозначается символом I. Закон Ома связывает ток, протекающий по проводнику, с напряжением V и сопротивлением R; то есть V = IR. Альтернативная формулировка закона Ома — I = V / R.
2. В чем измеряется ток?
Ампер (AM-пир) или ампер — это международная единица измерения силы тока.Он выражает количество электронов (иногда называемых «электрическим зарядом»), проходящих через точку в цепи за заданное время.
3. Как рассчитать текущий делитель?
Здесь эта основная схема делителя тока состоит из двух резисторов: R 1 и R 2 , включенных параллельно, которые разделяют ток питания или источника IS между ними на два отдельных тока IR1 и IR2, прежде чем снова соединиться вместе и вернуться к источник.
IT = IR1 + IR 2
IR 1 = IT — IR 2
IR 2 = IT — IR 1
4.Как найти ток в последовательной цепи?
В последовательной цепи сила тока или амплитуда тока остается постоянной и может быть рассчитана с использованием закона Ома V = I / R, в то время как напряжение падает на каждом резисторе, которое можно суммировать, чтобы получить общее сопротивление.
5. Какая формула рассчитывается по току в параллельной цепи?
Вы можете найти полное сопротивление в параллельной цепи по следующей формуле: 1 / Rt = 1 / R1 + 1 / R2 + 1 / R3 + … Если один из параллельных путей разорван, ток будет продолжать течь во всех другие пути.Потому что сумма токов по каждому пути равна общему току, протекающему от источника.
6. Разделен ли ток по параллельной цепи?
В параллельной цепи заряд разделяется на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей.
7.В сериях ток такой же?
Один и тот же ток протекает через каждую часть последовательной цепи. Общее сопротивление последовательной цепи равно сумме отдельных сопротивлений. Падение напряжения на резисторе в последовательной цепи прямо пропорционально размеру резистора. Если в какой-либо точке цепь разорвана, ток не будет течь.
8. В чем измеряется ток?
Ампер (AM-пир) или ампер — это международная единица измерения силы тока. Он выражает количество электронов (иногда называемых «электрическим зарядом»), проходящих через точку в цепи за заданное время.18 электронов (1 кулон) в секунду проходят через точку в цепи. Ампер в уравнениях обозначается буквой «I». Это аналогично увеличению напряжения, которое вызывает увеличение тока.
10. Постоянный ли параллельный ток?
Ток остается постоянным при последовательном подключении, а напряжение остается постоянным при параллельном подключении, ток подобен воде, текущей в реках, он всегда течет определенным путем и с постоянным количеством, но когда создается некоторое отклонение, он распределяется и количество постепенно уменьшается здесь с течением.
11. Разделен ли ток по последовательной цепи?
Один и тот же ток протекает через каждую часть последовательной цепи. Общее сопротивление последовательной цепи равно сумме отдельных сопротивлений. Напряжение, приложенное к последовательной цепи, равно сумме отдельных падений напряжения.
12. Постоянный ли параллельный ток?
Ток остается постоянным при последовательном подключении, а напряжение остается постоянным при параллельном подключении, ток подобен воде, текущей в реках, он всегда течет определенным путем и с постоянным количеством, но когда создается некоторое отклонение, он распределяется и количество постепенно уменьшается здесь с течением.
13. Какова действующая формула правила деления?
Таким образом, в правиле деления тока сказано, что ток в любой из параллельных ветвей равен отношению сопротивления противоположной ветви к общему сопротивлению, умноженному на общий ток.
14. Как делится ток в параллельной цепи?
В параллельной цепи заряд разделяется на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Сила тока вне ветвей равна сумме токов в отдельных ветвях.Это все еще та же величина тока, только разделенная на несколько путей.
15. Что такое схема делителя тока? Цепи делителя тока
— это параллельные цепи, в которых ток источника или питания делится на несколько параллельных цепей. Это приводит к различным путям и разветвлениям для тока, чтобы течь или проходить. Однако токи могут иметь разные значения через каждый компонент.
16. Что такое текущее правило делителя?
17. Когда можно использовать текущее деление?
Текущее правило деления, которое мы используем, когда в цепи существует несколько параллельных путей.Мы знаем, что напряжение на параллельном пути одинаковое, но ток делится. Предположим, что в цепи с напряжением питания V есть два параллельных пути, сопротивления которых равны R1, R2 ,.
18. Каков действующий закон распределения?
Закон распределения тока или правило разделения тока: Когда ток течет более чем по одному параллельному пути, каждый из путей разделяет определенную часть общего тока в зависимости от сопротивления / импеданса этого пути.
19.Какая ветка текущая?
Анализ тока ветви — это метод, используемый для расчета тока в каждой ветви. Анализ тока ветви использует комбинацию закона Кирхгофа по току и напряжению для получения набора линейных уравнений. Эти линейные уравнения затем решаются для получения значения тока, протекающего в ветвях.
20. Какова формула текущего закона Кирхгофа?
Текущий закон Кирхгофа (KCL) — это первый закон, который касается сохранения заряда, входящего и покидающего соединение.Другими словами, алгебраическая сумма ВСЕХ токов, входящих и выходящих из соединения, должна быть равна нулю: Σ I IN = Σ I OUT .
.

 Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;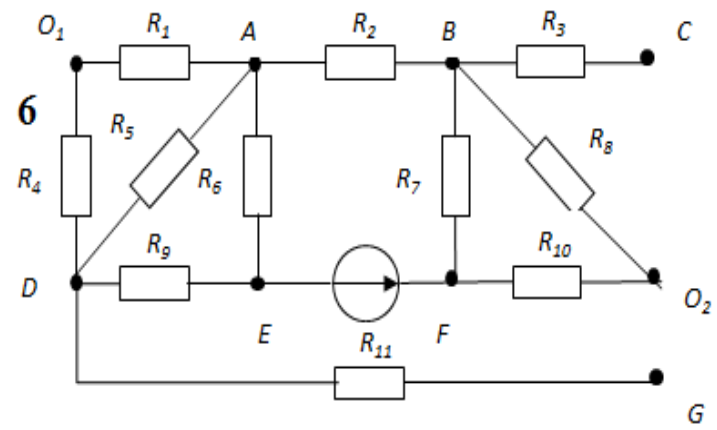

 времени τ RC и частота среза RC-фильтра
времени τ RC и частота среза RC-фильтра